Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x (người) là số thợ may lúc đầu của xí nghiệp.
Đến lúc chia vải thì có 3 người bị bệnh nên số thợ may còn lại là x - 3 (người).
Số mét vải chia đều cho mỗi thợ may lúc đầu là 1400/x (m)
Số mét vải chia đều cho mỗi thợ may sau khi có 3 người bị bệnh phải nghỉ là: (1400/x -3) - 6 (m).
Theo đề bài ta có phương trình: 1400/x = (1400/x - 3) - 6
Giải phương trình ta được: x1= 28 (nhận); x2= - 25 (loại).
Vậy lúc đầu xí nghiệp có tất cả 28 thợ may.

Gọi lúc đầu xí nghiệp dự định mỗi ngày may \(x\)bộ \(x>0\).
Xí nghiệp sẽ hoàn thành sau số ngày là: \(\frac{150}{x}\)(ngày)
Thực tế mỗi ngày may được số bộ là \(x+5\)(bộ)
Hoàn thành sau số ngày là: \(\frac{150}{x}-1\)(ngày).
Ta có: \(\left(x+5\right)\left(\frac{150}{x}-1\right)=150\)
\(\Leftrightarrow\frac{750}{x}-x-5=0\)
\(\Rightarrow-x^2-5x+750=0\)
\(\Leftrightarrow\left(x-25\right)\left(x+30\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=25\left(tm\right)\\x=-30\left(l\right)\end{cases}}\)
Vậy lúc đầu xí nghiệp dự định mỗi ngày may \(30\)bộ.

a: a*c<0
=>(1) có hai nghiệm phân biệt
b: Bạn viết lại biểu thức đi bạn

a: Khi m=1 thì pt sẽ là: x^2+4x-3=0
=>x=-2+căn 7 hoặc x=-2-căn 7
b: Δ=(2m-6)^2-4(m-4)
=4m^2-24m+36-4m+16
=4m^2-28m+52=(2m-7)^2+3>0
=>PT luôn có hai nghiệm pb
c: PT có hai nghiệm trái dấu
=>m-4<0
=>m<4

Câu 1
a) Xét phương trình : 2x2 +5x - 8 = 0
Có \(\Delta=5^2-4.2.\left(-8\right)=89>0\)
=> Phương trình luôn có 2 nghiệm phân biệt x1, x2
b) Do phương trình luôn có 2 nghiệm x1,x2
=> Theo định lí viet ta có: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{5}{2}\\x_1.x_2=-4\end{matrix}\right.\)
A = \(\dfrac{2}{x_1}+\dfrac{2}{x_2}=\dfrac{2.x_2}{x_1x_2}+\dfrac{2x_1}{x_1x_2}=\dfrac{2\left(x_1+x_2\right)}{x_1x_2}=\dfrac{2.\left(-\dfrac{5}{2}\right)}{-4}=\dfrac{-5}{-4}=\dfrac{5}{4}\)
Vậy A = \(\dfrac{5}{4}\)
Câu 2
Ta có \(P=\dfrac{a+4\sqrt{a}+4}{\sqrt{x}+2}+\dfrac{4-a}{2-\sqrt{a}}\left(a\ge0;a\ne4\right)\)
\(=\dfrac{\left(2+\sqrt{a}\right)^2}{2+\sqrt{a}}+\dfrac{\left(2-\sqrt{a}\right)\left(2+\sqrt{a}\right)}{2-\sqrt{a}}\)
\(=\sqrt{a}+2+\left(2+\sqrt{a}\right)=2\sqrt{a}+4\)
Vậy P = \(2\sqrt{a}+4\left(a\ge0;a\ne4\right)\)
b) Ta có a2 - 7a + 12 = 0
\(\Leftrightarrow a^2-4a-3a+12=0\)
\(\Leftrightarrow a\left(a-4\right)-3\left(a-4\right)=0\)
\(\Leftrightarrow\left(a-4\right)\left(a-3\right)=0\Leftrightarrow\left[{}\begin{matrix}a=4\left(loại\right)\\a=3\end{matrix}\right.\)
Với a = 3 thay vào P ta được P = \(2\sqrt{3}+4\)
\(\Rightarrow\sqrt{P}=\sqrt{2\sqrt{3}+4}=\sqrt{3+2\sqrt{3}+1}=\sqrt{\left(\sqrt{3}+1\right)^2}=\sqrt{3}+1\)
Vậy \(\sqrt{P}=\sqrt{3}+1\) tại a2 -7a + 12 =0

c) tim x1 và x2 theo ct;
x1= 16 +can denta ....tu lam
d) c/a <0
lam dc roi chu
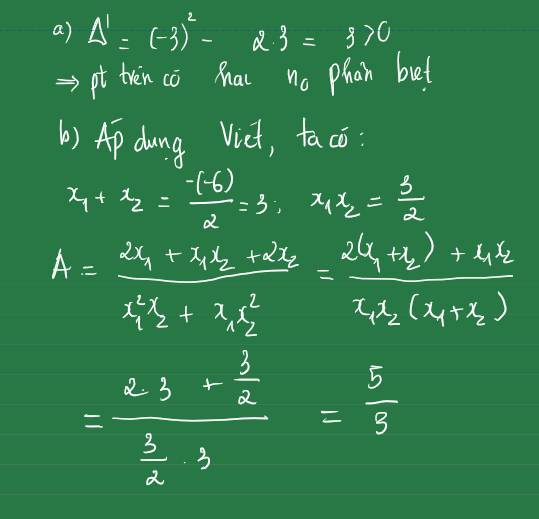

Câu 1:
\(ac=1.\left(-3\right)=-3< 0\Rightarrow\) pt luôn có 2 nghiệm pb trái dấu
Theo định lý Viet: \(\left\{{}\begin{matrix}x_1+x_2=-\frac{b}{a}=6\\x_1x_2=\frac{c}{a}=-3\end{matrix}\right.\)
c/ \(A=\left(2x_1-3\right)\left(2x_2-3\right)=4x_1x_2-6x_1-6x_2+9\)
\(A=4x_1x_2-6\left(x_1+x_2\right)+9\)
\(A=4.\left(-3\right)-6.6+9=-39\)
Câu 2:
Gọi số thợ may ban đầu là x người \(\left(x>3\right)\)
Số vải dự định cho mỗi người: \(\frac{400}{x}\) (m)
Sau khi 3 người nghỉ, số vải cho mỗi người: \(\frac{400}{x-3}\)
Ta có pt:
\(\frac{400}{x-3}-\frac{400}{x}=6\)
\(\Leftrightarrow6x\left(x-3\right)=400x-400\left(x-3\right)\)
\(\Leftrightarrow6x^2-18x-1200=0\)
Phương trình ko có nghiệm nguyên \(\Rightarrow\) đề sai
Cảm ơn khi giúp tôi làm bài câu 2 sai đề một xí nghiệp may dự định đem 1400m vải chứ không phải 400 thầy nhập lộn số liệu