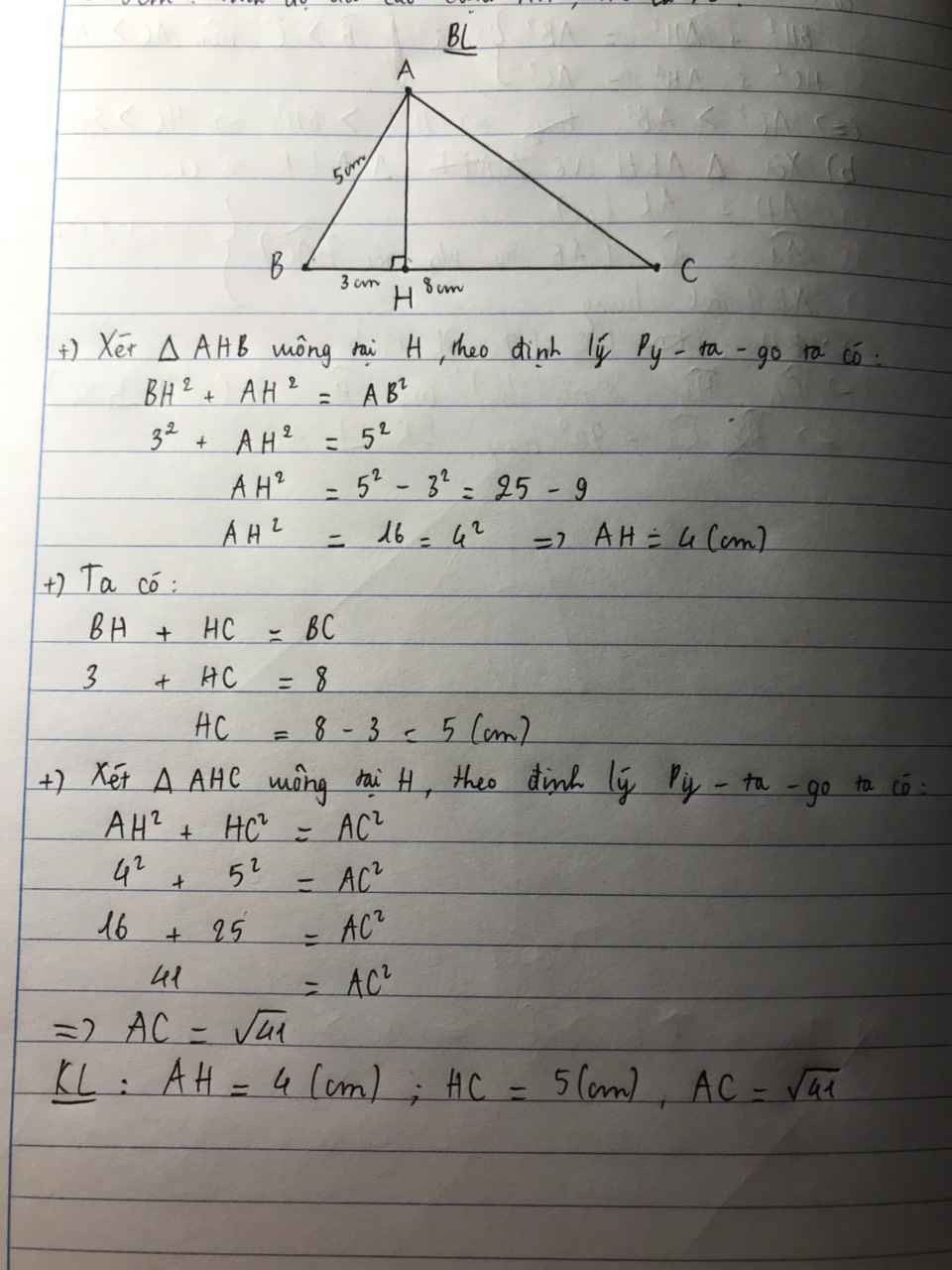
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
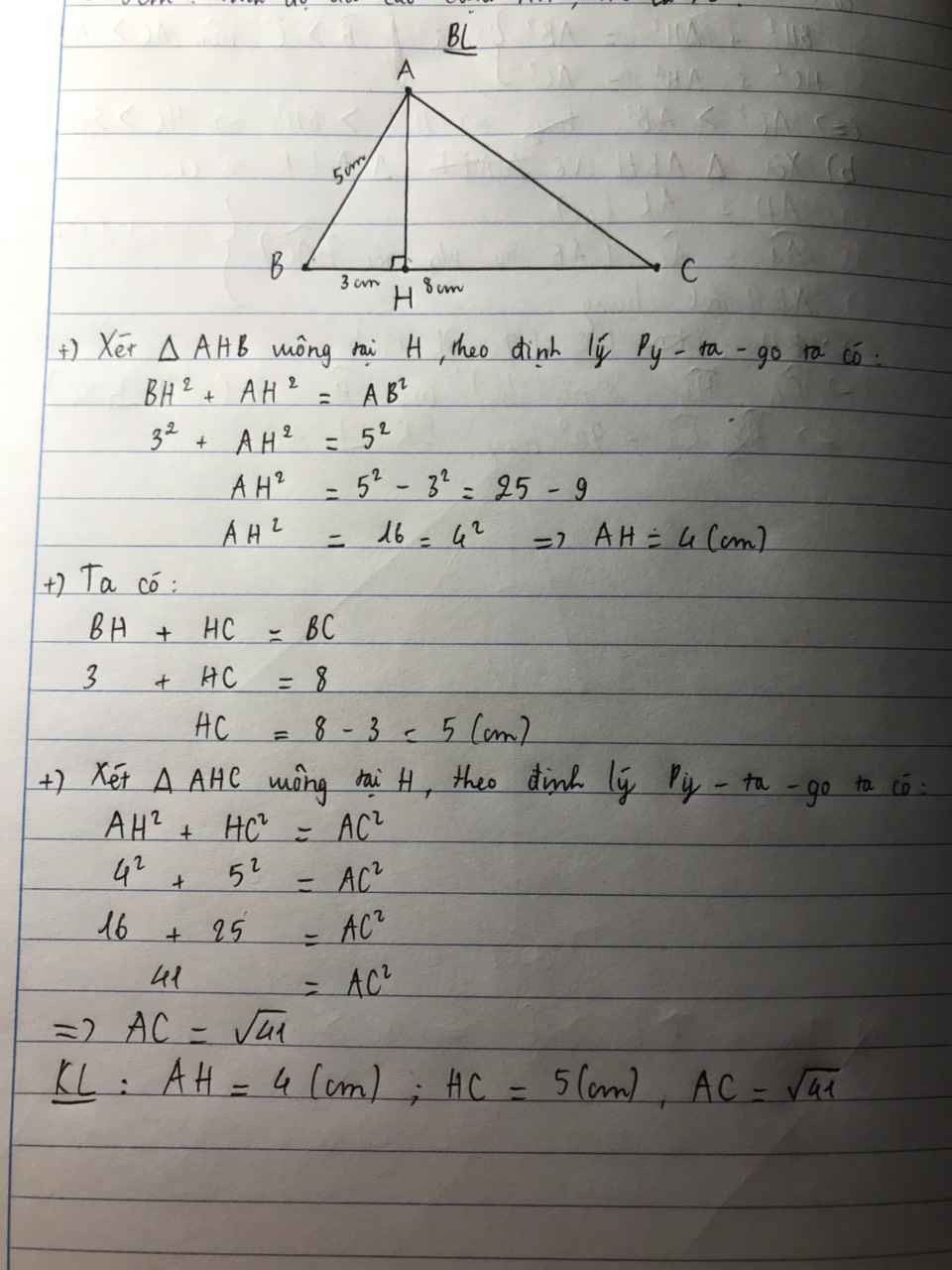
Hình bé tự vẽ nhá.
Áp dụng định lý Py-ta-go vào tam giác ABH vuông tại H,có :
AH2 +BH2 =AB2
AH2 = AB2 - BH2
AH2 = 52 - 32
=>. AH2 = 16
AH = 4 (cm)
Theo đề, có : AH vuông góc với BC
=> H thuộc BC
=> BH + HC = BC
HC = 8 - 3
HC = 5 (cm)
Áp dụng định lý Py-ta-go vào tam giác AHC vuông tại H, có :
AH2 + HC2 = AC2
42 + 52 = AC2
=> AC2 = 41
AC = \(\sqrt{41}\)
Áp dụng đ.lí pytago trong tam giác vuông ABH ta có;
AH2+BH2=AB2
=>AH2=AB2-BH2=52-32
=>AH2=25-9=16
=>AH=+(-)4
mà AH>0 =>AH=4 cm
Lại có;
BH+HC=BC
=>HC=BC-BH=8-3
=>HC=5 cm
Áp dụng đ.lí pytago trong tam giác vuông AHC ta có:
AC2=AH2+HC2
=>AC2=42+52=16+25
=>AC2=41
=>AC=+(-)\(\sqrt{41}\)
Mà AC >0 =>AC=\(\sqrt{41}\)cm
Vậy AH=4 cm; HC=5 cm ; AC= \(\sqrt{41}\)cm
- Ta có tam giác ABC vuông tại H
Áp dụng định lí Pi-ta-go có:
\(AB^2-BH^2=AH^2=5^2-3^2=16\Rightarrow AH=4\)
Tương tự ta có:...(bn tự làm)
Tam giác AHC vuông tại H
=> cũng như trên
Tự vẽ nhé
Áp dụng định lí Pi-ta-go vào tam giác ABH vuông tại H , ta có:
AH\(^2\)+ BH\(^2\)= AB\(^2\)
AH\(^2\)= \(AB^2-BH^2\)
\(AH^2=5^2-3^2\)
\(=>AH^2=16\)
\(AH=4cm\)
Theo đề, ta có: AH vuông góc với BC
=> H thuộc BC
=> BH + HC = BC
HC = 8 - 3
HC=5 cm
Áp dụng định lý Pi-ta-go vào tam giác AHC vuông tại H, ta có:
\(AH^2+HC^2=AC^2\)
\(4^2+5^2=AC^2\)
=> \(AC^2=41\)
=> \(AC=\sqrt{41}\)
hình bạn tự vẽ nha
Áp dụng định lý Py-ta-go vào tam giác ABH vuông tại H,có :
AH2 +BH2 =AB2
AH2 = AB2 - BH2
AH2 = 52 - 32
=>. AH2 = 16
AH = 4 (cm)
Theo đề, có : AH vuông góc với BC
=> H thuộc BC
=> BH + HC = BC
HC = 8 - 3
HC = 5 (cm)
Áp dụng định lý Py-ta-go vào tam giác AHC vuông tại H, có :
AH2 + HC2 = AC2
42 + 52 = AC2
=> AC2 = 41
AC = √41
XÉT \(\Delta ABH\)VUÔNG TẠI H
CÓ\(AB^2=AH^2+HB^2\)( ĐL PY-TA-GO)
THAY\(5^2=AH^2+3^2\)
\(25=AH^2+9\)
\(AH^2=25-9\)
\(AH^2=16\)
\(AH=\sqrt{16}=4\left(cm\right)\)
TA CÓ \(BH+HC=BC\)
\(3+HC=8\)
\(HC=5\left(cm\right)\)
xét \(\Delta AHC\)VUÔNG TẠI H
CÓ \(AC^2=AH^2+HC^2\)(ĐỊNH LÝ PYTAGO)
\(AC^2=4^2+5^2\)
\(AC^2=16+25\)
\(AC^2=41\)
\(AC=\sqrt{41}\)
Bạn tự vẽ hình nhé! Phần mềm trên này khó căn chuẩn
Vì \(AH\perp BC\Rightarrow\widehat{AHB}=\widehat{AHC}=90^0\)
Xét \(\Delta ABH\) có \(\widehat{AHB}=90^0\Rightarrow AH^2+BH^2=AB^2\) ( ĐL Pytago )
Thay số : \(\Rightarrow AH^2+3^2=5^2\Leftrightarrow AH^2=5^2-3^2=25-9=16\Leftrightarrow AH=4\left(cm\right)\)
Có \(BH+HC=BC\Rightarrow HC=BC-BH=8-3=5\left(cm\right)\)
Vì \(\Delta AHC\) có \(\widehat{AHC}=90^0\Rightarrow AH^2+HC^2=AC^2\) ( ĐL Pytago )
\(\Rightarrow AC^2=4^2+5^2=16+25=41\Leftrightarrow AC=\sqrt{41}\left(cm\right)\)
Xét \(\Delta ABH\)vuông tại H \(\Rightarrow AH^2+BH^2=AB^2\)
\(\Rightarrow AH^2=AB^2-BH^2=5^2-3^2=25-9=16\)
\(\Rightarrow AH=4\left(cm\right)\)
Ta có: \(BH+CH=BC\)\(\Rightarrow HC=BC-BH=8-3=5\)( cm )
Xét \(\Delta AHC\)vuông tại H \(\Rightarrow AH^2+HC^2=AC^2\)
\(\Rightarrow AC^2=AH^2+HC^2=4^2+5^2=16+25=40\)
\(\Rightarrow AC=\sqrt{40}=2\sqrt{10}\)( cm )
Áp dụng đ.lí pytago trong tam giác vuông ABH ta có;
AH2+BH2=AB2
=>AH2=AB2-BH2=52-32
=>AH2=25-9=16
=>AH=+(-)4
mà AH>0 =>AH=4 cm
Lại có;
BH+HC=BC
=>HC=BC-BH=8-3
=>HC=5 cm
Áp dụng đ.lí pytago trong tam giác vuông AHC ta có:
AC2=AH2+HC2
=>AC2=42+52=16+25
=>AC2=41
=>AC=+(-)√41
Mà AC >0 =>AC=√41cm
Vậy AH=4 cm; HC=5 cm ; AC= √41cm
cho tam giác ABC , kẻ AH vuông góc với BC . biết AB=5cm , BH=8cm . tính độ dài các cạnh AH , HC , AC
Bạn tham khảo nhé!
https://olm.vn/hoi-dap/detail/33236210534.html
a. Ta có: ∠HAC + ∠AHC + ∠C = 180 ( ĐL tổng 3 góc tam giác )
∠HAC + 90 + 30 = 180
∠HAC = 180 - ( 30 + 90 )
∠HAC = 180 - 120 = 60
b. -Ta có: BC = HC + HB
10 = HC + 3
⇒ HC = 10 - 3 = 7 ( cm )
-ΔAHB ⊥ tại H ( đường cao AH )
⇒ AB² = AH² + BH² ( ĐL Py-ta-go )
5² = AH² + 3²
25 = AH² + 9
⇒AH² = 25 - 9 = 16
⇒AH = √16 = 4 ( cm )
-ΔAHC ⊥ tại H ( đường cao AH )
⇒ AC² = AH² + CH² ( ĐL Py-ta-go )
AC² = 4² + 7²
AC² = 16 + 49 = 65
⇒AC = √65 ( cm )
Câu 1:
Xét tam giác ABH vuông tại H, ta có:
AB2 = AH2 + HB2 (định lý Py-ta-go)
202 = AH2 + 162
400 = AH2 + 256
AH2 = 400 - 256
AH2 = 144
AH = \(\sqrt{144}\)= 12 (cm)
Xét tam giác AHC vuông tại H, ta có:
AC2 = AH2 + HC2 (định lý Py-ta-go)
AC2 = 122 + 52
AC2 = 144 + 25
AC2 = 169
AC = \(\sqrt{169}\)= 13 (cm)
Vậy AH = 12 cm
AC = 13 cm
Bài 2:
Xét tam giác AHC vuông tại H, ta có:
AC2 = AH2 + HC2 (định lý Py-ta-go)
152 = AH2 + 92
225 = AH2 + 81
AH2 = 225 - 81
AH2 = 144
AH = \(\sqrt{144}\)= 12 (cm)
Xét tam giác AHB vuông tại, ta có:
AB2 = AH2 + HB2 (định lý Py-ta-go)
AB2 = 122 + 52
AB2 = 144 + 25
AB2 = 169
AB = \(\sqrt{169}\)= 13 (cm)
Vậy AB = 13 cm
