Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn A.
Phương pháp: Cạnh huyền là đường kính đáy.
Cách giải:
THeo đề bài, đường kính của hình tròn đáy của nón bằng 2a. Vậy bán kính R = a.
Chiều cao của hình nón bằng chiều cao của tam giác đều, nên h = a√3 và
đường sinh l = = 2a.
Vậy diện tích xung quanh của hình nón là:
Sxq = πRl = 2a2π ( đơn vị diện tích).
Thể tích khối nón là:
.
Câu hỏi nào của Võ Nguyễn Thái cũng có Võ Đoong Anh Tuấn làm,có khúc mắc
Áp dụng BĐT tam giác ta có:
a+b>c =>c-a<b =>c2-2ac+a2<b2
a+c>b =>b-c <a =>b2-2bc+c2<a2
b+c>a =>a-b<c =>a2-2ab+b2<c2
Suy ra: c2-2ac+a2+b2-2bc+c2+a2-2ab+b2<a2+b2+c2
<=>-2.(ab+bc+ca)+2.(a2+b2+c2)<a2+b2+c2
<=>-2(ab+bc+ca)<-(a2+b2+c2)
<=>2.(ab+bc+ca)<a2+b2+c2
Đáp án C
Theo bài ra, khối nón (N) có r = a 3 h = a 3 ⇒ V N = 1 3 π r 2 h = 1 3 π a 3 2 a 3 = 3 π a 3 .
Đáp án C.
Bán kính đáy của hình nón là r = 2 a 3 2 = a 3 , chiều cao hình nón là h = 1 2 , cạnh huyền = a 3 .
Thể tích tích V của khối nón (N) là V = 1 3 π r 2 h = π a 3 3 .
vì (C) đi qua điểm A nên tọa độ điểm A thỏa mãn pt \(y=\frac{ax^2-bx}{x-1}\) ta có \(\frac{5}{2}=\frac{a+b}{-2}\Rightarrow a+b=-5\)
vì tiếp tuyến của đồ thị tại điểm O có hệ số góc =-3 suy ra y'(O)=-3
ta có \(y'=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\) ta có y'(O)=b=-3 suy ra a=-2
vậy ta tìm đc a và b
Đáp án C
Phương pháp: Diện tích xung quanh của hình nón: S x q = π R l
Trong đó : R bán kính đáy, l độ dài đường sinh.
Cách giải: Tam giác ABC vuông cân tại A, AH ⊥ BC
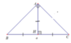
=> AH = HB = HC
Diện tích xung quanh của hình nón:
S x q = π R l
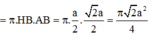
Đáp án D
Phương pháp: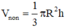
trong đó R; h lần lượt là bán kính đáy và chiều cao của khối nón.
Cách giải: Ta có