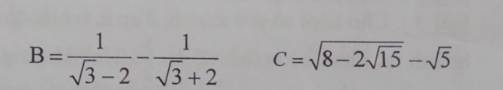K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
mong mn giúp em, em cần gấp
3 tháng 7 2021
Dạng 2:
a) \(\left(1-\cos\alpha\right)\left(1+\cos\alpha\right)=1-\cos^2\alpha=\sin^2\alpha\)
b) \(\sin\alpha-\sin\alpha\cdot\cos^2\alpha=\sin\alpha\left(1-\cos^2\alpha\right)=\sin^3\alpha\)
c) Ta có: \(\sin^4\alpha+\cos^4\alpha+2\cdot\sin^2\alpha\cdot\cos^2\alpha\)
\(=\left(\sin^2\alpha+\cos^2\alpha\right)^2\)
\(=1^2=1\)
d) Ta có: \(\tan^2\alpha-\sin^2\alpha\cdot\tan^2\alpha\)
\(=\tan^2\alpha\left(1-\sin^2\alpha\right)\)
\(=\tan^2\alpha\cdot\cos^2\alpha\)
\(=\dfrac{\sin^2\alpha}{\cos^2\alpha}\cdot\cos^2\alpha=\sin^2\alpha\)
R
0
LT
1
31 tháng 12 2023
\(B=\dfrac{1}{\sqrt{3}-2}-\dfrac{1}{\sqrt{3}+2}\)
\(=\dfrac{\sqrt{3}+2-\left(\sqrt{3}-2\right)}{\left(\sqrt{3}-2\right)\left(\sqrt{3}+2\right)}\)
\(=\dfrac{\sqrt{3}+2-\sqrt{3}+2}{3-4}=\dfrac{4}{-1}=-4\)
\(C=\sqrt{8-2\sqrt{15}}-\sqrt{5}\)
\(=\sqrt{5-2\cdot\sqrt{5}\cdot\sqrt{3}+3}-\sqrt{5}\)
\(=\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}-\sqrt{5}\)
\(=\sqrt{5}-\sqrt{3}-\sqrt{5}=-\sqrt{3}\)
V
1
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 9 2021
ĐKXĐ: \(x\ge1\)
\(\sqrt{x-1-4\sqrt{x-1}+4}+\sqrt{x-1-6\sqrt{x-1}+9}=0\)
\(\Leftrightarrow\sqrt{\left(\sqrt{x-1}-2\right)^2}+\sqrt{\left(3-\sqrt{x-1}\right)^2}=0\)
\(\Leftrightarrow\left|\sqrt{x-1}-2\right|+\left|3-\sqrt{x-1}\right|=0\)
Do \(\left|\sqrt{x-1}-2\right|+\left|3-\sqrt{x-1}\right|\ge\left|\sqrt{x-1}-2+3-\sqrt{x-1}\right|=1>0\) với mọi x thuộc TXĐ
\(\Rightarrow\) Phương trình đã cho vô nghiệm
22 tháng 10 2023
36B
37C
38D
39B
40D
41A
42B
43B
44A
45B
46B
47A
48C
50B
51B
52B
53D
54C
55D
56C
15 tháng 8 2019
( a + b ) ( a + c ) = 8 hay a2 + ab + ac + bc = 8
\(\Rightarrow\)a ( a + b + c ) + bc = 8
\(\sqrt{abc\left(a+b+c\right)}=\sqrt{a\left(a+b+c\right).bc}\le\frac{a\left(a+b+c\right)+bc}{2}=4\)
\(\Rightarrow abc\left(a+b+c\right)\le16\)
Vậy GTLN của A là 16