Question

[Pham Trong Bach]

Cần đẽo thanh gỗ hình hộp có đáy là hình vuông thành hình trụ có cùng chiều cao. Tỉ lệ thể tích gỗ cần phải đẽo đi ít nhất (tính gần đúng) là

A. 21%

B. 11%

C. 50%

D. 30%

Answer 1

[Cao Minh Tâm]

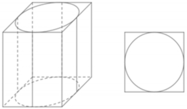
Đáp án A

Giả sử cạnh hình vuông là a. Để lượng gỗ đẽo đi ít nhất thì diện tích hình tròn đáy lớn nhất khi và chỉ khi đường tròn tiếp xúc với các cạnh hình vuông  ⇒ R = a 2

Diện tích đáy hình tròn :  S 1 = πR 2

Diện tích đáy hình hộp: S 2 = a 2 = 4 R 2

Chiều cao bằng nhau nên tỉ lệ thể tích bằng tỉ lệ diện tích đáy:  S 1 S 2 = π 4

Tỉ lệ thể tích cần đẽo đi ít nhất là: 1 - π 4 ≈ 21 %