
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: Xét ΔABE và ΔDBE có
BA=BD
\(\widehat{ABE}=\widehat{DBE}\)
BE chung
Do đó: ΔABE=ΔDBE
Suy ra: \(\widehat{BAE}=\widehat{BDE}=90^0\)
b: Xét ΔAEF vuông tại A và ΔDEC vuông tại D có
EA=ED
\(\widehat{AEF}=\widehat{DEC}\)
Do đó: ΔAEF=ΔDEC
c: Xét ΔEFC có EF=EC
nên ΔEFC cân tại E
d: Ta có: ΔAEF=ΔDEC
nên AF=DC
Ta có: BA+AF=BF
BD+DC=BC
mà BA=BD
và AF=DC
nên BF=BC
hay B nằm trên đường trung trực của CF(1)
Ta có: EF=EC
nên E nằm trên đường trung trực của CF(2)
Ta có: NF=NC
nên N nằm trên đường trung trực của CF(3)
Từ (1), (2) và (3) suy ra B,E,N thẳng hàng

Đây là bài bạn phải nộp cho thầy nên mình sẽ không làm chi tiết. Nhưng mình có thể gợi ý cho bạn như sau:
1.
Đối với tỉ lệ thức đã cho, mỗi phân số ta nhân cả tử và mẫu với 4, 3, 2. Khi đó, ta thu được 1 tỉ lệ thức mới
Dùng tỉ lệ thức trên, áp dụng tính chất dãy tỉ số bằng nhau (cộng), ta thu được $12x=8y=6z(*)$
Tiếp tục áp dụng tính chất dãy tỉ số bằng nhau cho $(*)$ dựa theo điều kiện $x+y+z=18$ ta sẽ tính được $x,y,z$ thỏa mãn.
2.
Áp dụng tính chất dãy tỉ số bằng nhau (cộng) cho 3 phân số đầu tiên, ta sẽ tìm được tổng $x+y+z$
Khi tìm được tổng $x+y+z$, cộng vào 3 phân số đầu tiên trong bài, mỗi phân số cộng thêm 1. Khi đó, ta thu được tỉ lệ thức $\frac{m}{x}=\frac{n}{y}=\frac{p}{z}(*)$ với $m,n,p$ đã tính được dựa theo giá trị $x+y+z$.
Áp dụng tính chất dãy tỉ số bằng nhau cho tỉ lệ thức $(*)$, kết hợp với kết quả $x+y+z$ thì bài toán đã rất quen thuộc rồi.

\(a,\Rightarrow2x=-\dfrac{13}{15}\Rightarrow x=-\dfrac{13}{30}\\ b,\Rightarrow x=\dfrac{-12\cdot15}{4}=-45\)

Bài 37:
\(\dfrac{\left|x-2016\right|+2017}{\left|x-2016\right|+2018}=1-\dfrac{1}{\left|x-2016\right|+2018}\ge1-\dfrac{1}{2018}=\dfrac{2017}{2018}\) (vì \(\left|x-2016\right|\ge0\))
-Dấu bằng xảy ra \(\Leftrightarrow x=2016\)
Bài 38:
-Áp dụng t/c của dãy tỉ số bằng nhau ta có:\(\dfrac{a+b-c}{c}=\dfrac{b+c-a}{a}=\dfrac{c+a-b}{b}=\dfrac{a+b-c+b+c-a+c+a-b}{c+a+b}=\dfrac{2\left(c+a+b\right)}{c+a+b}=2\)\(\Rightarrow\dfrac{a+b-c}{c}=2\Rightarrow a+b-c=2c\Rightarrow a+b+c=4c\)
\(\dfrac{b+c-a}{a}=2\Rightarrow b+c-a=2a\Rightarrow a+b+c=4a\)
\(\dfrac{c+a-b}{b}=2\Rightarrow c+a-b=2b\Rightarrow a+b+c=4b\)
\(\Rightarrow4a=4b=4c\Rightarrow a=b=c\)
\(B=\left(1+\dfrac{b}{a}\right)\left(1+\dfrac{a}{c}\right)\left(1+\dfrac{c}{b}\right)=\left(1+1\right)\left(1+1\right)\left(1+1\right)=2.2.2=8\)
Bài 39:
-Thay \(x=-2;y=\dfrac{1}{2}\) vào A ta được:\(A=-2.\dfrac{1}{2}+\left(-2\right)^2.\dfrac{1}{2^2}+\left(-2\right)^4.\dfrac{1}{2^4}+\left(-2\right)^6.\dfrac{1}{2^6}+...+\left(-2\right)^{2016}.\dfrac{1}{2^{2016}}+\left(-2\right)^{2018}.\dfrac{1}{2^{2018}}\)
\(=-1+2^2.\dfrac{1}{2^2}+2^4.\dfrac{1}{2^4}+2^6.\dfrac{1}{2^6}+...+2^{2016}.\dfrac{1}{2^{2016}}+2^{2018}.\dfrac{1}{2^{2018}}\)
\(=-1+1+1+1+...+1+1\) (có \(\dfrac{2018-2}{2}+1=1009\) số 1)
\(=-1.1009.1=1008\)
Bài 40:
\(25-y^2=8\left(x-2019\right)^2\)
\(\Rightarrow8\left(x-2019\right)^2-25=-y^2\le0\)
\(\Rightarrow0\le\left(x-2019\right)^2\le\dfrac{25}{8}\)
Mà x là số nguyên nên \(\left(x-2019\right)^2\) là số chính phương.
\(\Rightarrow\left(x-2019\right)^2=0\) hay \(\left(x-2019\right)^2=1\)
\(\Rightarrow x=2019\) hay \(x=2018\) hay \(x=2020\)
*\(x=2019\)\(\Rightarrow25-y^2=8\left(2019-2019\right)^2\Rightarrow25-y^2=0\Rightarrow y^2=25\Rightarrow y=5\) hay
\(y=-5\) (nhận)
*\(x=2018\)\(\Rightarrow25-y^2=8\left(2018-2019\right)^2\Rightarrow25-y^2=8\Rightarrow y^2=17\Rightarrow y=\sqrt{17}\)
hay \(y=-\sqrt{17}\)
*\(x=2020\)\(\Rightarrow25-y^2=8\left(2020-2019\right)^2\Rightarrow25-y^2=8\Rightarrow y^2=17\Rightarrow y=\sqrt{17}\)
hay \(y=-\sqrt{17}\)
-Vậy \(x=2019\) và \(y=5\) hay \(y=-5\)

h: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x^2}{9}=\dfrac{y^2}{16}=\dfrac{x^2+y^2}{9+16}=\dfrac{100}{25}=4\)
Do đó: \(\left\{{}\begin{matrix}x\in\left\{6;-6\right\}\\y\in\left\{8;-8\right\}\end{matrix}\right.\)

9. a) \(\dfrac{4}{3}+\dfrac{2}{3}:x=-\dfrac{2}{5}\)
\(\Rightarrow\dfrac{2}{3}:x=-\dfrac{26}{15}\)\(\Rightarrow x=\dfrac{2}{3}:\left(-\dfrac{26}{15}\right)=-\dfrac{5}{13}\)
b) \(\dfrac{7}{3}-1\dfrac{3}{5}.x=-1\dfrac{2}{3}\)
\(\Rightarrow\dfrac{8}{5}x=\dfrac{7}{3}-\left(-\dfrac{5}{3}\right)=\dfrac{7+5}{3}\)
\(\Rightarrow\dfrac{8}{5}x=4\Leftrightarrow x=\dfrac{5}{2}\)
c) \(\left(-2\dfrac{1}{4}:x+1,5\right)\left(\dfrac{-5}{3}.x-\dfrac{5}{12}\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}-2\dfrac{1}{4}:x=-1.5\\\dfrac{-5}{3}.x=\dfrac{5}{12}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-\dfrac{1}{4}\end{matrix}\right.\)
d) \(-\dfrac{3}{5}.x-\left(x+2,5\right)=-\dfrac{13}{15}\)
\(\Rightarrow-\dfrac{8}{5}.x=-\dfrac{13}{15}+2,5\)
\(\Rightarrow-\dfrac{8}{5}.x=\dfrac{49}{30}\)
\(\Rightarrow x=\dfrac{49}{30}:\left(\dfrac{-8}{5}\right)=-\dfrac{49}{48}\)
10.
a) \(\left(-3+\dfrac{3}{x}-\dfrac{1}{3}\right):\left(1+\dfrac{2}{5}+\dfrac{2}{3}\right)=-\dfrac{5}{4}\)
\(\Rightarrow\left(\dfrac{3}{x}-\dfrac{10}{3}\right):\dfrac{31}{15}=-\dfrac{5}{4}\)
\(\Rightarrow\dfrac{3}{x}-\dfrac{10}{3}=-\dfrac{5}{4}.\dfrac{31}{15}=-\dfrac{31}{12}\)
\(\Rightarrow\dfrac{3}{x}=-\dfrac{31}{12}+\dfrac{10}{3}=\dfrac{3}{4}\)
\(\Leftrightarrow x=4\)
b) \(\left(\dfrac{2}{5}-x\right):1\dfrac{1}{3}+\dfrac{1}{2}=-4\)
\(\Rightarrow\left(\dfrac{2}{5}-x\right):\dfrac{4}{3}=-4-\dfrac{1}{2}=-\dfrac{9}{2}\)
\(\Rightarrow\dfrac{2}{5}-x=-\dfrac{9}{2}.\dfrac{4}{3}=-6\)
\(\Rightarrow x=\dfrac{2}{5}-\left(-6\right)=\dfrac{32}{5}\)
c) \(-\dfrac{3x}{4}.\left(\dfrac{1}{x}+\dfrac{2}{7}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}-\dfrac{3x}{4}=0\\\dfrac{1}{x}+\dfrac{2}{7}=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\\dfrac{1}{x}=-\dfrac{2}{7}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{7}{2}\end{matrix}\right.\)
d) \(2,5x+\dfrac{-4}{7}=\dfrac{1}{2}x\)
\(\Rightarrow2,5x-\dfrac{1}{2}x=\dfrac{4}{7}\)
\(\Rightarrow2x=\dfrac{4}{7}\Leftrightarrow x=\dfrac{2}{7}\)

a, \(A=\left(\dfrac{8}{3}xy^2\right).\left(\dfrac{-1}{4}x^2y^5\right).\left(10x^5y^7\right)^0\)
⇒\(A=\dfrac{8}{3}xy^2.\dfrac{-1}{4}x^2y^5.1\)
⇒\(A=\left(\dfrac{8}{3}.\dfrac{-1}{4}.1\right).\left(x.x^2\right).\left(y^2.y^5\right)\)
⇒\(A=\dfrac{-2}{3}x^3y^7\)
+)Hệ số: \(\dfrac{-2}{3}\)
+)Bậc:10
b, Thay \(x=2\), \(y=-1\) vào A ta có:
\(A=\dfrac{-2}{3}.2^3.\left(-1\right)^7\)
⇒\(A=\dfrac{-2}{3}.8.\left(-1\right)\)
⇒\(A=\dfrac{16}{3}\)
Vậy \(A=\dfrac{16}{3}\) khi \(x=2,y=-1\)

 các bạn giải hộ mik nha,cảm ơn ơn các bạn nhiều !!!
các bạn giải hộ mik nha,cảm ơn ơn các bạn nhiều !!!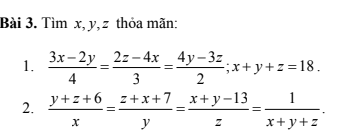
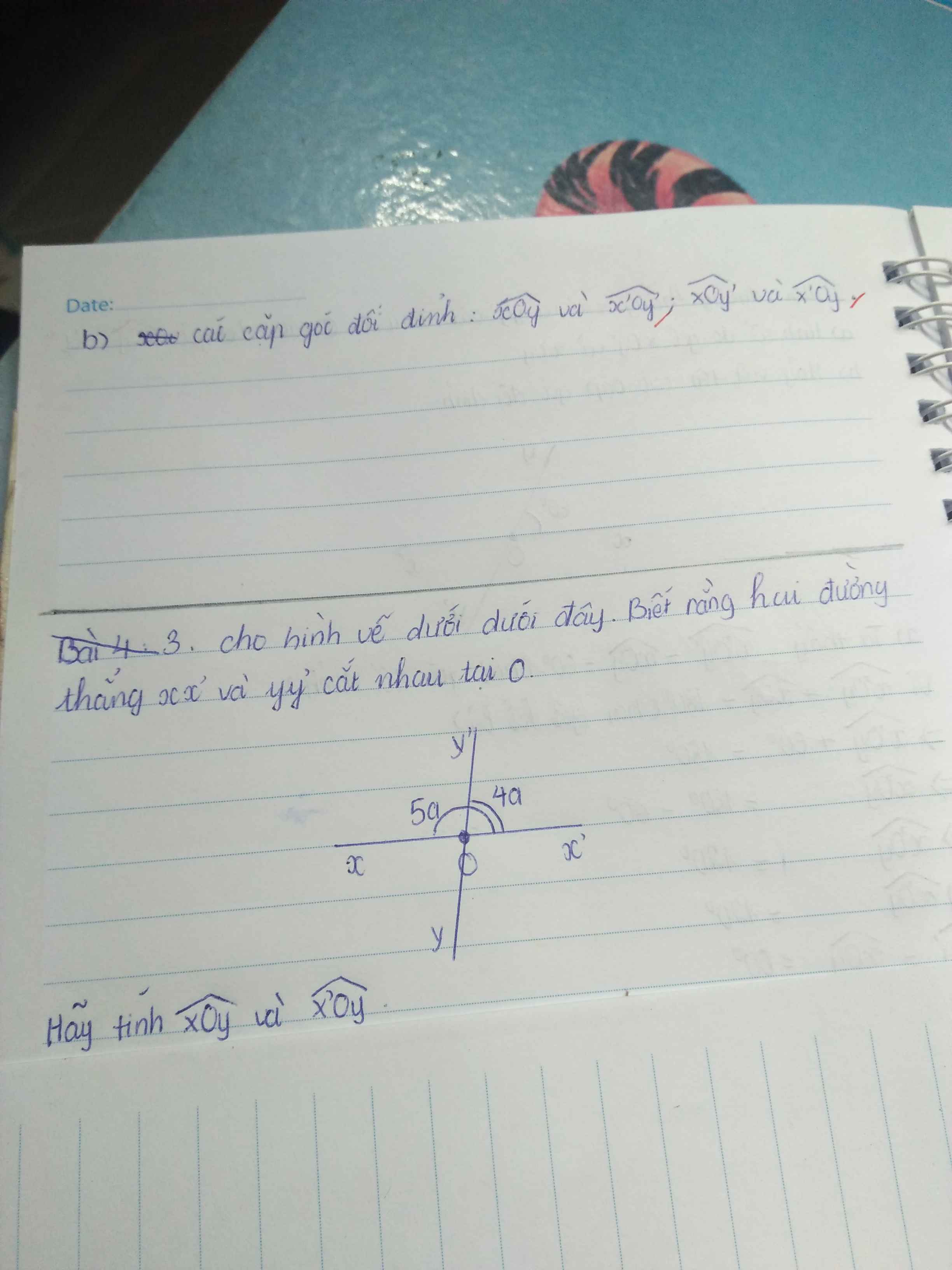
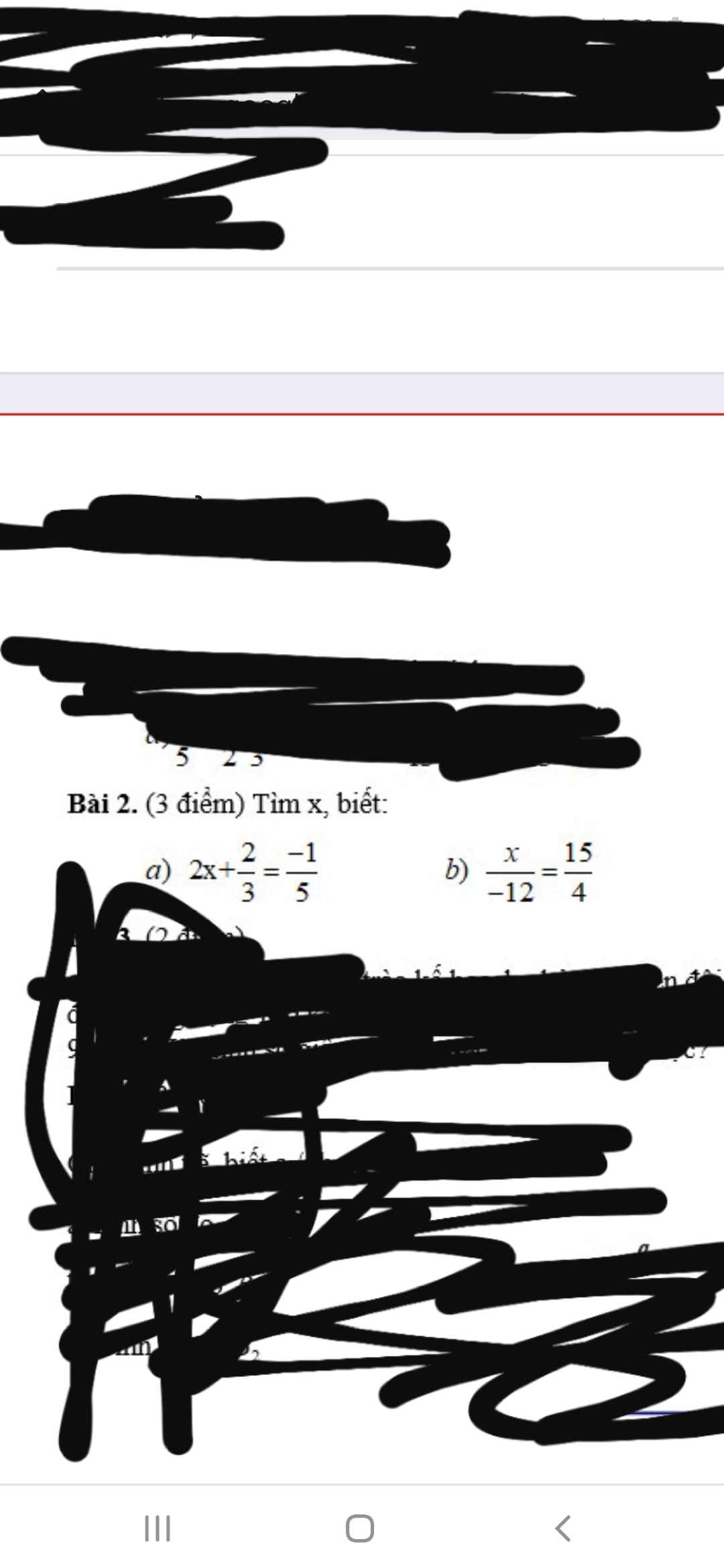
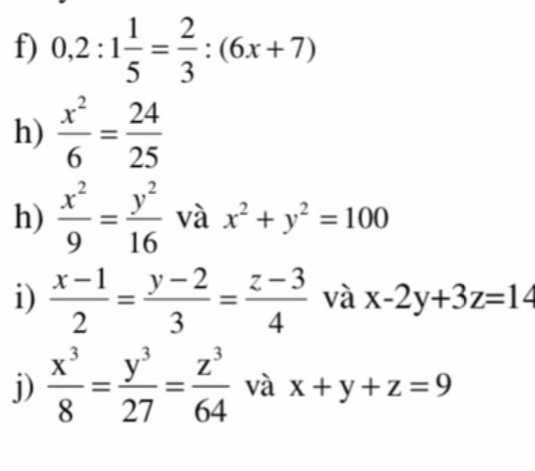
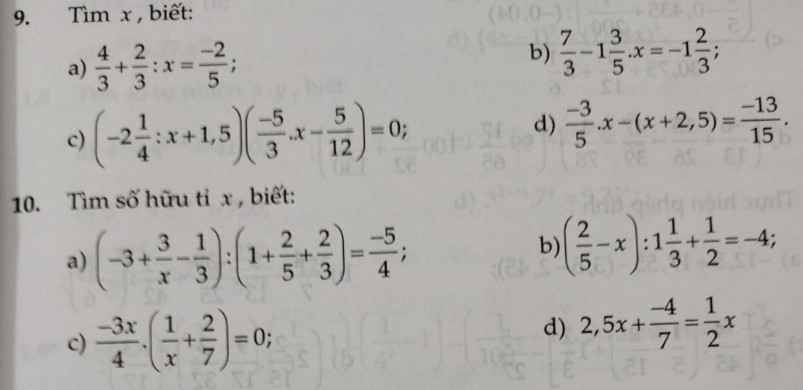 Giúp em với . Em cảm ơn nhiều
Giúp em với . Em cảm ơn nhiều 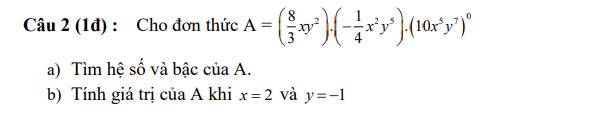 giúp mình với, mình cảm ơn nhiều
giúp mình với, mình cảm ơn nhiều
BẠN T I C K CHO MIK NHÉ
thanks
thank you
là sao bạn??