
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Các em đăng câu hỏi lên diễn đàn thì cần đăng đầy đủ nội dung câu hỏi lên trên này. Có như vậy mọi người mới biết yêu cầu của đề bài và trợ giúp các em tốt nhất. Cảm ơn các em đã đồng hành cùng Olm.

2:
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
b: BA=BE
DA=DE
=>BD là trung trực của AE
c: DA=DE
DE<DC
=>DA<DC
4:
a: ΔABC cân tại A có AI là phân giác
nên AI vuông góc BC tại I
b: Xét ΔABC có
CM,AI là trung tuyến
CM cắt AI tại G
=>G là trọng tâm
=>BG là trung tuyến của ΔABC
c: BI=CI=9cm
=>AI=căn 15^2-9^2=12cm
=>GI=1/3*12=4cm

Bài 2:
a: Ta có: Om là tia phân giác của \(\widehat{xOy}\)
nên \(\widehat{xOm}=\widehat{yOm}=\dfrac{180^0}{2}=90^0\)
Do đó: Om\(\perp\)xy
b: Ta có: \(\widehat{xOa}+\widehat{mOa}=90^0\)
\(\widehat{mOb}+\widehat{yOb}=90^0\)
mà \(\widehat{mOa}=\widehat{yOb}\)
nên \(\widehat{xOa}=\widehat{mOb}\)

Bài 7:
a: Sửa đề: Tính góc ABD
Xét ΔMAC và ΔMDB có
MA=MD
\(\widehat{AMC}=\widehat{DMB}\)(hai góc đối đỉnh)
MC=MB
Do đó: ΔMAC=ΔMDB
=>\(\widehat{MAC}=\widehat{MDB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//BD
Ta có: AC//BD
AC\(\perp\)AB
Do đó: BD\(\perp\)AB
=>\(\widehat{ABD}=90^0\)
b: Ta có: ΔMAC=ΔMDB
=>AC=BD
Xét ΔBAC vuông tại A và ΔABD vuông tại B có
AB chung
AC=BD
Do đó: ΔBAC=ΔABD
c: Ta có: ΔBAC=ΔABD
=>BC=AD
mà \(AM=\dfrac{1}{2}AD\)
nên \(AM=\dfrac{1}{2}BC\)
Bài 8:
a: ta có: BC=BD
B nằm giữa D và C(BD và BC là hai tia đối nhau)
Do đó: B là trung điểm của DC
AB và AE là hai tia đối nhau
=>A nằm giữa B và E
=>\(BE=BA+AE=2AB+AB=3AB\)
=>\(\dfrac{EA}{EB}=\dfrac{2AB}{3AB}=\dfrac{2}{3}\)
Xét ΔEDC có
EB là đường trung tuyến
\(EA=\dfrac{2}{3}EB\)
Do đó: A là trọng tâm của ΔEDC
b: Xét ΔEDC có
A là trọng tâm
nên CA đi qua trung điểm của DE

Lời giải:
Áp dụng BĐT dạng $|a|+|b|\geq |a+b|$ ta có:
$|x+2020|+|x+2021|=|x+2020|+|-(x+2021)|$
$\geq |x+2020-(x+2021)|=1$
Vậy GTNN của biểu thức là $1$. Giá trị này đạt tại $(x+2020).-(x+2021)\geq 0$
$(x+2020)(x+2021)\leq 0$
$-2021\leq x\leq -2020$


Bài 1 :
Thay x = 2 ; y = -1/2 ta được
\(B=-8+2.4\left(-\dfrac{1}{2}\right)-4.2.\left(\dfrac{1}{4}\right)+2\left(-\dfrac{1}{2}\right)-3\)
\(=-8-4-2-1-3=-18\)

a: \(P=-\left|5-x\right|+2019\le2019\forall x\)
Dấu '=' xảy ra khi x=5


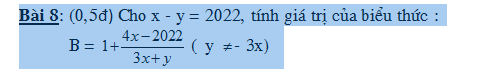 mọi người giúp mình với ạ, mai mình đi thi thi. Cảm ơn mọi người nhiều
mọi người giúp mình với ạ, mai mình đi thi thi. Cảm ơn mọi người nhiều 
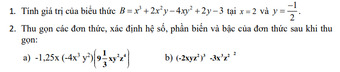

Bài 37:
\(\dfrac{\left|x-2016\right|+2017}{\left|x-2016\right|+2018}=1-\dfrac{1}{\left|x-2016\right|+2018}\ge1-\dfrac{1}{2018}=\dfrac{2017}{2018}\) (vì \(\left|x-2016\right|\ge0\))
-Dấu bằng xảy ra \(\Leftrightarrow x=2016\)
Bài 38:
-Áp dụng t/c của dãy tỉ số bằng nhau ta có:\(\dfrac{a+b-c}{c}=\dfrac{b+c-a}{a}=\dfrac{c+a-b}{b}=\dfrac{a+b-c+b+c-a+c+a-b}{c+a+b}=\dfrac{2\left(c+a+b\right)}{c+a+b}=2\)\(\Rightarrow\dfrac{a+b-c}{c}=2\Rightarrow a+b-c=2c\Rightarrow a+b+c=4c\)
\(\dfrac{b+c-a}{a}=2\Rightarrow b+c-a=2a\Rightarrow a+b+c=4a\)
\(\dfrac{c+a-b}{b}=2\Rightarrow c+a-b=2b\Rightarrow a+b+c=4b\)
\(\Rightarrow4a=4b=4c\Rightarrow a=b=c\)
\(B=\left(1+\dfrac{b}{a}\right)\left(1+\dfrac{a}{c}\right)\left(1+\dfrac{c}{b}\right)=\left(1+1\right)\left(1+1\right)\left(1+1\right)=2.2.2=8\)
Bài 39:
-Thay \(x=-2;y=\dfrac{1}{2}\) vào A ta được:\(A=-2.\dfrac{1}{2}+\left(-2\right)^2.\dfrac{1}{2^2}+\left(-2\right)^4.\dfrac{1}{2^4}+\left(-2\right)^6.\dfrac{1}{2^6}+...+\left(-2\right)^{2016}.\dfrac{1}{2^{2016}}+\left(-2\right)^{2018}.\dfrac{1}{2^{2018}}\)
\(=-1+2^2.\dfrac{1}{2^2}+2^4.\dfrac{1}{2^4}+2^6.\dfrac{1}{2^6}+...+2^{2016}.\dfrac{1}{2^{2016}}+2^{2018}.\dfrac{1}{2^{2018}}\)
\(=-1+1+1+1+...+1+1\) (có \(\dfrac{2018-2}{2}+1=1009\) số 1)
\(=-1.1009.1=1008\)
Bài 40:
\(25-y^2=8\left(x-2019\right)^2\)
\(\Rightarrow8\left(x-2019\right)^2-25=-y^2\le0\)
\(\Rightarrow0\le\left(x-2019\right)^2\le\dfrac{25}{8}\)
Mà x là số nguyên nên \(\left(x-2019\right)^2\) là số chính phương.
\(\Rightarrow\left(x-2019\right)^2=0\) hay \(\left(x-2019\right)^2=1\)
\(\Rightarrow x=2019\) hay \(x=2018\) hay \(x=2020\)
*\(x=2019\)\(\Rightarrow25-y^2=8\left(2019-2019\right)^2\Rightarrow25-y^2=0\Rightarrow y^2=25\Rightarrow y=5\) hay
\(y=-5\) (nhận)
*\(x=2018\)\(\Rightarrow25-y^2=8\left(2018-2019\right)^2\Rightarrow25-y^2=8\Rightarrow y^2=17\Rightarrow y=\sqrt{17}\)
hay \(y=-\sqrt{17}\)
*\(x=2020\)\(\Rightarrow25-y^2=8\left(2020-2019\right)^2\Rightarrow25-y^2=8\Rightarrow y^2=17\Rightarrow y=\sqrt{17}\)
hay \(y=-\sqrt{17}\)
-Vậy \(x=2019\) và \(y=5\) hay \(y=-5\)