Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương pháp:
TH1: An và Cường trả lời đúng, Bình trả lời sai.
TH2: Bình và Cường trả lời đúng, An trả lời sai.
Áp dụng quy tắc cộng.
Cách giải:
TH1: An và Cường trả lời đúng, Bình trả lời sai => P1 = 0,9.(1 - 0,7).0,8 = 0,216
TH2: Bình và Cường trả lời đúng, An trả lời sai => P2 = (1 - 0,9).0,7.0,8 = 0,056
Vậy xác suất cô giáo chỉ kiểm tra bài cũ đúng 3 bạn trên là P = P1 + P2 = 0,272

Không gian mẫu là số cách gọi ngẫu nhiên 2 nam, 2 nữ từ 46 học sinh.
Suy ra số phần tử của không gian mẫu là ![]() .
.
Gọi A là biến cố 4 học sinh (2 nam, 2 nữ) được gọi lên đều không chuẩn bị bài tập về nhà, trong đó có Bình và Mai . Ta mô tả khả năng thuận lợi cho biến cố A như sau:
● Gọi Bình và Mai lên bảng, có 1 cách.
● Tiếp theo gọi 1 bạn nam từ 6 bạn không làm bài tập về nhà còn lại và 1 bạn nữ từ 3 bạn không làm bài tập về nhà còn lại, có ![]() cách.
cách.
Suy ra số phần tử của biến cố A là 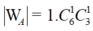 .
.
Vậy xác suất cần tính 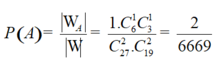 .
.
Chon C.

Trong mỗi khối, XS hs trượt Toán là 0,25; trượt Lý là 0,15; trượt cả 2 môn là 0,1; trượt đúng 1 môn là 0,2; chỉ trượt Toán là 0,15; chỉ trượt Lý là 0,05; trượt ít nhất 1 môn là 0,3; ko trượt môn nào là 0,7
a) P = 0,25^2 = 0,0625
b) Câu này đề chưa rõ ràng, có nhiều cách hiểu
..1) 2 hs đó đều bị trượt ít nhất 1 môn
..2) 2 hs đó cùng bị trượt trong 1 môn nào đó (còn môn kia không trượt)
..3) 2 hs đó cùng bị trượt trong 1 môn nào đó (còn môn kia có thể trượt hoặc không)
..Nếu hiểu theo cách 1 thì P = 0,3^2 = 0,09
..Nếu hiểu theo cách 2 thì P = 0,15^2 + 0,05^2 = 0,025
..Nếu hiểu theo cách 3 thì P = 0,25^2 + 0,15^2 - 0,1^2 = 0,075
c) P = 0,7^2 = 0,49
d) Trường hợp này là biến cố đối lập với biến cố c
..P = 1 - 0,7^2 = 0,51

Kí hiệu A 1 , A 2 , A 3 lần lượt là các biến cố: Học sinh được chọn từ khối I trượt Toán, Lí, Hoá: B 1 , B 2 , B 3 lần lượt là các biến cố : Học sinh được chọn từ khối II trượt Toán, Lí, Hoá. Rõ ràng với mọi (i,j), các biến cố A i và B i độc lập.
a) 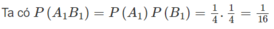
b) Xác suất cần tính là
P ( ( A 1 ∪ A 2 ∪ A 2 ) ∩ ( B 1 ∪ B 2 ∪ B 3 ) ) = P ( A 1 ∪ A 2 ∪ A 2 ) . P ( B 1 ∪ B 2 ∪ B 3 ) = 1 / 2 . 1 / 2 = 1 / 4
c) Đặt A = A 1 ∪ A 2 ∪ A 3 , B = B 1 ∪ B 2 ∪ B 3
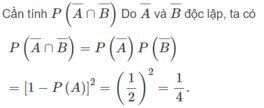
d) Cần tính P(A ∪ B)
Ta có
P(A ∪ B) = P(A) + P(B) − P(AB)
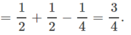

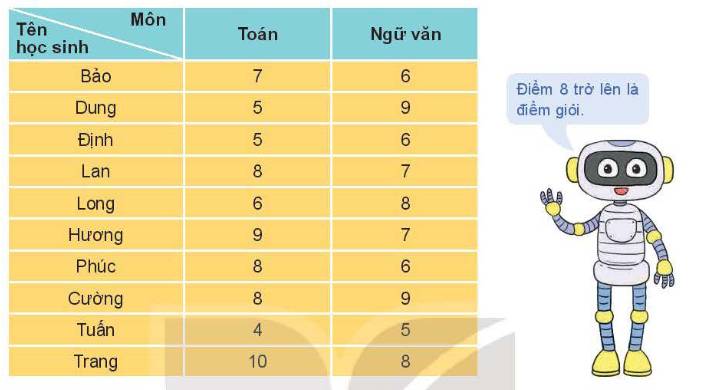
a) A = {Dung, Long, Cường, Trang}
B = {Lan, Hương, Phúc, Cường, Trang}
C = {Dung, Long, Lan, Hương, Phúc, Cường, Trang}
b) A ∪ B = {Dung, Long, Cường, Trang, Lan, Hương, Phúc}
a: A={Dung, Long, Cường, Trang}
B={Lan, Hương, Phúc, Cường, Trang}
C={Dung, Long, Lan, Hương, Phúc, Cường, Trang}
b: A hợp B={Dung,Long,Cường,Trang,Phúc,Hương,Lan}
ừ đúng đó bn
rất đúng