Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
Dây bị vướng tại vị trí cân bằng → E 1 = E 2 → m g l 1 α 1 2 2 = m g l 2 α 2 2 2 → α 2 = α 1 l 1 l 2

\(T_1=2\pi\sqrt{\dfrac{l_1}{g}}\left(1\right),T_2=2\pi\sqrt{\dfrac{l_2}{g}}\left(2\right)\)
\(T=2\pi\sqrt{\dfrac{l_1-l_2}{g}}\left(3\right)\)
Thay (1),(2) vào (3) ta được:
\(T=\sqrt{T_1^2-T_2^2}=1.5s\) ->C

Đáp án B
Phương pháp: Sử dụng công thức tính chu kì con lắc đơn
Cách giải :
Chu kì dao của con lắc đơn:
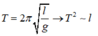
Khi con lắc có chiều dài l1 thì T12 ~ l1 ; khi con lắc có chiều dài l2 thì T2 2 ~ l2
Do đó khi con lắc có chiều dài l thì T 2 ~ l
Mà l = l1 + l2 → T2 = T12 + T22 = 0,62 + 0,82 = 1→ T = 1s
Chú ý: Nếu l = l1 + l2 thì T2 = T12 – T22

Chu kì của con lắc đơn phụ thuộc vào l, g và biên độ góc không phụ thuộc vào khối lượng m. T không đổi khi thay đổi khối lượng m của con lắc.
Chọn đáp án D.

Tăng 4 lần nhé bạn
Vì T = \(2\pi.\sqrt{\dfrac{l}{g}}\) nên T tỉ lệ với \(\sqrt{l}\)
Có nghĩa là nếu l tăng 16 lần thì T sẽ tăng \(\sqrt{16}\) lần, tức là 4 lần đấy!
Và hãy suy nghĩ kĩ lại nhá, bài này cũng không khó đâu!

Đáp án D
+ Chu kì con lắc đơn dao động nhỏ là
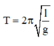
® không phụ thuộc vào khối lượng
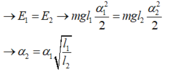
Một con lắc đơn dao động với biên độ góc \(\alpha\) nhỏ. Chu kì con lắc phụ thuộc vào cả chiều dài và vị trí nơi đặt con lắc trên mặt đất.
Khi đó chu kì áp dụng theo công thức: \(T=2\pi\cdot\sqrt{\dfrac{l}{g}}\)
Với chiều dài \(l\) không đổi và tỉ lệ với \(T^2\).
Một con lắc đơn dao đọng với biên độ góc a nhỏ.Chu kì con lắc phụ thuộc vào cả chiều dài và vị trí nơi đặt con lắc trên mặt đất.
Khi đó chu kì áp dụng theo công thức:\(\overline{T+2\pi.\sqrt{\dfrac{l}{g}}}\)
Với chiều dài \(\overline{l}\)không đổi và tỉ lệ với\(^{T^2}\)