Mặt Trời
Bách khoa toàn thư mở Wikipedia
Jump to navigationJump to search

Mặt Trời 
 |
| Các dữ liệu quan trắc |
|---|
Khoảng cách trung bình
từ Trái Đất | 149,6 ×106 km
(92,95×106 dặm) |
| Cấp sao biểu kiến (V) | −26,74m[1] |
| Cấp sao tuyệt đối | 4,83m[1] |
| Phân loại quang phổ | G2V |
| Độ kim loại | Z = 0,0177[2] |
| Kích thước góc | 31,6′ - 32,7′[3] |
| Các thông số quỹ đạo |
|---|
Khoảng cách trung bình
từ trung tâm Ngân Hà | 2,5×1017 km
(26.000 năm ánh sáng) |
| Chu kỳ trong Ngân Hà | ~ 2,25-2,50×108 năm |
| Vận tốc bay quanh tâm Ngân Hà | 217 km/s |
| Các thông số vật lý |
|---|
| Đường kính trung bình | 1,392 ×106 km[1]
109 lần Trái Đất |
| Độ dẹt | 9×10-6 |
| Diện tích bề mặt | 6,0877 ×1012 km²
(11.900 lần Trái Đất) |
| Thể tích | 1,4122 ×1018 km³
(1.300.000 lần Trái Đất) |
| Khối lượng | 1,9891 ×1030 kg
(332.946 lần Trái Đất) |
| Tỷ trọng (trung bình) | 1,408 g/cm³ |
| Gia tốc trọng trường (tại bề mặt) | 273,95 m s-2
(27,9 g) |
| Vận tốc thoát ly | 617,54 km/s |
| Nhiệt độ bề mặt | 5.780 K |
| Nhiệt độ nhật hoa | 5 triệu K |
| Nhiệt độ tâm (ước tính) | 13,6 triệu K |
| Độ sáng (LS) | 3,846×1026 W[1] |
| Suất bức xạ (IS) | 2,009×107 W m-2 sr-1 |
| Các thông số tự quay |
|---|
| Độ nghiêng trục quay | 7,25°
(tới mặt phẳng hoàng đạo)
67,23°
(tới mặt phẳng Ngân Hà) |
Xích kinh
tại cực bắc[4] | 286,13°
(19 h 4 m 31,2 s) |
Xích vĩ
tại cực bắc | 63,87° |
Chu kỳ tự quay
tại 16 °
tại xích đạo
tại cực | 25,38 ngày[1]
(25 ngày 9 h 7 ' 13 s)[4]
25,05 ngày[1]
34,3 ngày[1] |
Vận tốc tự quay
tại xích đạo | 7.284 km/h |
| Thành phần |
|---|
| Hiđrô | 73,46%[5] |
| Hêli | 24,85% |
| Ôxy | 0,77% |
| Cacbon | 0,29% |
| Sắt | 0,16% |
| Lưu huỳnh | 0,12% |
| Neon | 0,12% |
| Nitơ | 0,09% |
| Silic | 0,07% |
| Magiê | 0,05% |
Mặt Trời là ngôi sao ở trung tâm Hệ Mặt Trời, chiếm khoảng 99,86% khối lượng của Hệ Mặt Trời.[6] Trái Đất và các thiên thể khác như các hành tinh, tiểu hành tinh, thiên thạch, sao chổi, và bụi quay quanh Mặt Trời. Khoảng cách trung bình giữa Mặt Trời và Trái Đất xấp xỉ 149,6 triệu kilômét (1 Đơn vị thiên văn AU) nên ánh sáng Mặt Trời cần 8 phút 19 giây mới đến được Trái Đất. Trong một năm, khoảng cách này thay đổi từ 147,1 triệu kilômét (0,9833 AU) ở điểm cận nhật (khoảng ngày 3 tháng 1), tới xa nhất là 152,1 triệu kilômét (1,017 AU) ở điểm viễn nhật (khoảng ngày 4 tháng 7).[7] Năng lượng Mặt Trời ở dạng ánh sáng hỗ trợ cho hầu hết sự sống trên Trái Đất thông qua quá trình quang hợp,[8] và điều khiển khí hậu cũng như thời tiếttrên Trái Đất. Thành phần của Mặt Trời gồm hydro (khoảng 74% khối lượng, hay 92% thể tích), heli (khoảng 24% khối lượng, 7% thể tích), và một lượng nhỏ các nguyên tố khác, gồm sắt, nickel, oxy, silic, lưu huỳnh, magiê, carbon, neon, canxi, và crom.[9] Mặt Trời có hạng quang phổ G2V. G2 có nghĩa nó có nhiệt độ bề mặt xấp xỉ 5.778 K (5.505 °C) khiến nó có màu trắng, và thường có màu vàng khi nhìn từ bề mặt Trái Đất bởi sự tán xạ khí quyển. Chính sự tán xạ này của ánh sáng ở giới hạn cuối màu xanh của quang phổ khiến bầu trời có màu xanh.[10] Quang phổ Mặt Trời có chứa các vạch ion hoá và kim loại trung tính cũng như các đường hydro rất yếu. V (số 5 La Mã) trong lớp quang phổ thể hiện rằng Mặt Trời, như hầu hết các ngôi sao khác, là một ngôi sao thuộc dãy chính. Điều này có nghĩa nó tạo ra năng lượng bằng tổng hợp hạt nhân của hạt nhân hydro thành heli. Có hơn 100 triệu ngôi sao lớp G2 trong Ngân Hà của chúng ta. Từng bị coi là một ngôi sao nhỏ và khá tầm thường nhưng thực tế theo hiểu biết hiện tại, Mặt Trời sáng hơn 85% các ngôi sao trong Ngân Hà với đa số là các sao lùn đỏ.[11][12]
Quầng nóng của Mặt Trời liên tục mở rộng trong không gian và tạo ra gió Mặt Trời là các dòng hạt có vận tốc gấp 5 lần âm thanh - mở rộng nhật mãn (Heliopause) tới khoảng cách xấp xỉ 100 AU. Bong bóng trong môi trường liên sao được hình thành bởi gió mặt trời, nhật quyển (heliosphere) là cấu trúc liên tục lớn nhất trong Hệ Mặt Trời.[13][14]
Mặt Trời hiện đang đi xuyên qua đám mây Liên sao Địa phương (Local Interstellar Cloud) trong vùng Bóng Địa phương(Local Bubble) mật độ thấp của khí khuếch tán nhiệt độ cao, ở vành trong của Nhánh Orion của Ngân Hà, giữa nhánh Perseus và nhánh Sagittarius của ngân hà. Trong 50 hệ sao gần nhất bên trong 17 năm ánh sáng từ Trái Đất, Mặt Trời xếp hạng 4[15] về khối lượng như một ngôi sao cấp bốn (M = +4,83),[1][16] dù có một số giá trị cấp hơi khác biệt đã được đưa ra, ví dụ 4,85[17] và 4,81.[18] Mặt Trời quay quanh trung tâm của Ngân Hà ở khoảng cách xấp xỉ 24.000–26.000 năm ánh sáng từ trung tâm Ngân Hà, nói chung di chuyển theo hướng chùm sao Cygnus và hoàn thành một vòng trong khoảng 225–250 triệu năm (một năm ngân hà). Tốc độ trên quỹ đạo của nó được cho khoảng 250 ± 20, km/s nhưng một ước tính mới đưa ra con số 251 km/s.[19][20] Bởi Ngân Hà của chúng ta đang di chuyển so với Màn bức xạ vi sóng vũ trụ (CMB) theo hướng chòm sao Hydra với tốc độ 550 km/s, nên tốc độ chuyển động của nó so với CMB là khoảng 370 km/s theo hướng chòm sao Crater hay Leo.[21]
Mục lục
- 1Đặc điểm
- 1.1Lõi
- 1.2Vùng bức xạ
- 1.3Vùng đối lưu
- 1.4Quang quyển
- 1.5Khí quyển
- 1.5.1Hàn quyển
- 1.5.2Sắc quyển (chromosphere)
- 1.5.3Vùng chuyển tiếp
- 1.5.4Vành nhật hoa
- 1.5.5Nhật quyển
- 1.6Từ trường
- 2Thành phần hóa học
- 2.1Các nguyên tố nhóm sắt bị ion hóa
- 2.2Quan hệ sự phân tầng khối lượng giữa hành tinh và Mặt Trời
- 3Các chu kỳ trên Mặt Trời
- 3.1Các vết đen Mặt Trời
- 3.2Chu kỳ dài
- 4Vị trí và chuyển động trong dải Ngân Hà
- 5Các vấn đề về các học thuyết
- 5.1Neutrino Mặt Trời
- 5.2Nhiệt độ vành nhật hoa
- 5.3Sao trẻ
- 5.4Các dị thường hiện tại
- 6Thám hiểm Mặt Trời
- 6.1Những hiểu biết trước đây
- 6.2Sư hiểu biết cùng với tiến bộ khoa học
- 6.2.1Trước Công nguyên
- 6.2.2Công nguyên
- 6.2.3Thuyết nhật tâm
- 6.2.4Thiên văn học hiện đại
- 6.3Các nhiệm vụ khám phá không gian
- 7Mặt Trời là nguồn năng lượng khổng lồ
- 8Mặt Trời và tác hại đến mắt
- 9Vòng đời của Mặt Trời
- 9.1Thời gian biểu tiến hóa sao của Mặt Trời và hệ Mặt Trời
- 10Trong văn hóa
- 11Xem thêm
- 12Ghi chú
- 13Tham khảo
- 14Liên kết ngoài
- 14.1Tiếng Anh
- 14.2Tiếng Việt
Đặc điểm[sửa | sửa mã nguồn]

Mặt Trăng đi qua Mặt Trời 2/2007,
được chụp bằng camera tử ngoại

Mô hình cấu trúc Mặt Trời:
1. Lõi
2. Vùng bức xạ
3. Vùng đối lưu
4. Quang quyển
5. Sắc quyển
6. Vành nhật hoa (Quầng)
7. Vết đen Mặt Trời
8. Hạt quang quyển (Đốm)
9. Vòng plasma
Mặt Trời là một ngôi sao thuộc dãy chính màu vàng chiếm khoảng 99% tổng khối lượng Hệ Mặt Trời. Nó là một hình cầu gần hoàn hảo, chỉ hơi dẹt khoảng chín phần triệu,[22]có nghĩa đường kính cực của nó khác biệt so với đường kính xích đạo chỉ 10 km (6 dặm). Bởi Mặt Trời tồn tại ở dạng trạng thái plasma và không rắn chắc do đó tốc độ quay (vận tốc góc) tại xích đạo nhanh hơn ở hai cực. Điều này được gọi là chuyển động không đồng tốc. Chu kỳ của chuyển động thực này xấp xỉ 25,6 ngày ở xích đạovà 33,5 ngày ở cực. Tuy nhiên, vì điểm quan sát thuận lợi luôn thay đổi khi Trái Đấtquay quanh Mặt Trời nên chuyển động biểu kiến của ngôi sao này tại xích đạo là khoảng 28 ngày.[23] Hiệu ứng ly tâm của chuyển động chậm này yếu hơn 18 triệu lần so với lực hấp dẫn tại xích đạo Mặt Trời. Hiệu ứng thủy triều của các hành tinh thậm chí còn yếu hơn, và không ảnh hưởng lớn tới hình dạng Mặt Trời.[24]
Mặt Trời là một sao nhóm I, nhóm sao có nhiều nguyên tố nặng.[note 1] Sự hình thành Mặt Trời có thể đã được bắt đầu từ các sóng chấn động từ một hay nhiều siêu tân tinh bên cạnh.[25] Lý thuyết này được đưa ra do sự phong phú của nguyên tố nặngtrong Hệ Mặt Trời, như vàng và uranium, nếu những sao có nhiều nguyên tố này thì gọi là Sao nhóm II (ít nguyên tố nặng). Các nguyên tố này theo khả năng có thể nhất đã được tạo ra bởi các phản ứng hạt nhân thu năng lượng trong một quá trình hình thành sao siêu mới, hay bởi sự biến đổi thông qua hấp thụ neutron bên trong một ngôi sao lớn thế hệ hai.[26]
Cấu trúc của Mặt Trời không có ranh giới cụ thể như những hành tinh đá: ở phần phía ngoài của nó, mật độ các khí giảm gần như theo hàm mũ theo khoảng cách từ tâm.[27] Tuy nhiên, cấu trúc bên trong của nó được xác định rõ ràng, như được miêu tả bên dưới. Bán kính Mặt Trời được đo từ tâm tới cạnh ngoài quang quyển. Đây đơn giản là lớp mà bên trên nó các khí quá lạnh hay quá mỏng để bức xạ một lượng ánh sáng đáng kể, và vì thế là bề mặt dễ quan sát nhất bằng mắt thường.[28]
Phía trong Mặt Trời không thể được quan sát trực tiếp và chính Mặt Trời là vật chắn bức xạ điện từ. Tuy nhiên, tương tự như trong địa chất học sử dụng sóng do các trận động đất tạo ra để xác định cấu trúc bên trong của Trái Đất, ngành nhật chấn học(helioseismology) sử dụng các sóng ngoại âm (infrasound) đi xuyên qua phần trong Mặt Trời để đo và hình dung cấu trúc bên trong của ngôi sao.[29] Mô hình máy tính về Mặt Trời cũng sử dụng một công cụ lý thuyết để xác định các lớp bên trong của nó.
Lõi[sửa | sửa mã nguồn]
Bài chi tiết: Lõi Mặt Trời

Mặt cắt ngang một ngôi sao kiểu Mặt Trời (hình vẽ bởi NASA)

Dãy phản ứng p-p giải phóng bức xạ điện từ gamma, neutrino
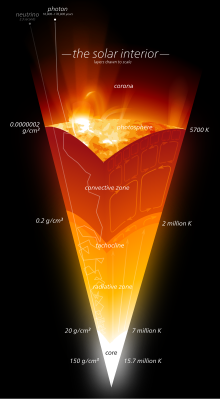
Mặt cắt cấu trúc của Mặt Trời
Lõi của Mặt Trời được coi là chiếm khoảng 0,2 tới 0,25 bán kính Mặt Trời.[30] Nó có mật độ lên tới 150g/cm³[31][32] (150 lần mật độ nước trên Trái Đất) và có nhiệt độ gần 13.600.000 độ K (so với nhiệt độ bề mặt Mặt Trời khoảng 5.800 K).[33] Những phân tích gần đây của phi vụ SOHO cho thấy tốc độ tự quay của lõi cao hơn vùng bức xạ.[30]Trong hầu hết vòng đời của Mặt Trời, năng lượng được tạo ra bởi phản ứng tổng hợp hạt nhân thông qua một loạt bước được gọi là dãy p–p (proton–proton) (xem hình bên phải) để biến hydro thành heli.[34] Chưa tới 2% heli được tạo ra trong Mặt Trời có từ chu trình CNO (Cacbon-Nitơ-Ôxy). Lõi là vùng duy nhất trong Mặt Trời tạo ra một lượng đáng kể nhiệt thông qua phản ứng tổng hợp: phần còn lại của ngôi sao được đốt nóng bởi năng lượng truyền ra ngoài từ lõi. Tất cả năng lượng được tạo ra từ phản ứng tổng hợp hạt nhân trong lõi phải đi qua nhiều lớp để tới quang quyển trước khi đi vào không gian dưới dạng ánh sáng Mặt Trời hay động năng của các hạt.[35][36]
Tốc độ phản ứng tổng hợp hạt nhân phụ thuộc nhiều vào mật độ và nhiệt độ, vì tốc độ phản ứng tổng hợp hạt nhân diễn ra ở lõi trong trạng thái cân bằng tự điều chỉnh: nếu tốc độ phản ứng hơi lớn hơn sẽ khiến lõi nóng lên nhiều và hơi mở rộng chống lại trọng lượng của các lớp bên ngoài, làm giảm tốc độ phản ứng và điều chỉnh sự nhiễu loạn; và nếu tốc độ hơi nhỏ hơn sẽ khiến lõi lạnh đi và hơi co lại, làm tăng tốc độ phản ứng và một lần nữa lại đưa nó về mức cũ.[37] Các photon (tia gamma) nhiều năng lượng phát ra trong các phản ứng tổng hợp hạt nhân bị hấp thụ trong một plasma mặt trời chỉ vài millimét, và sau đó tái phát xạ theo hướng ngẫu nhiên (và ở mức năng lượng khá thấp)—vì thế cần một thời gian dài các bức xạ mới lên tới bề mặt Mặt Trời. Những ước tính về "thời gian di chuyển của photon" trong khoảng từ 10.000 tới 170.000 năm.[38] Sau chuyến du hành cuối cùng qua lớp đối lưu bên ngoài để tới "bề mặt" trong suốt của quang quyển, các photon thoát ra như ánh sáng khả kiến. Mỗi tia gamma trong lõi Mặt Trời được chuyển thành hàng triệu photon ánh sáng nhìn thấy được trước khi đi vào không gian. Các neutrino cũng được phát sinh từ các phản ứng tổng hợp hạt nhân trong lõi, nhưng không giống như photon, chúng hiếm khi tương tác với vật chất, vì thế hầu như toàn bộ chúng thoát khỏi Mặt Trời ngay lập tức. Trong nhiều năm những đo đạc về số lượng neutrino do Mặt Trời tạo ra cho kết quả thấp hơn các dự đoán lý thuyết khoảng 3 lần. Sự không nhất quán này gần đây đã được giải quyết thông qua sự khám phá các hiệu ứng dao động neutrino. Vì trên thực tế Mặt Trời toả ra số lượng neutrino như các lý thuyết dự đoán, nhưng các máy dò tìm neutrino để lọt mất 2/3 trong số chúng bởi vì các neutrino đã thay đổi hương.[39]
Vùng bức xạ[sửa | sửa mã nguồn]
Trong vùng từ 0,25 tới khoảng 0,7 bán kính Mặt Trời, vật liệu Mặt Trời đủ nóng và đặc đủ để bức xạ nhiệt chuyển được nhiệt độ từ trong lõi ra ngoài.[40] Trong vùng này không có đối lưu nhiệt; tuy các vật liệu lạnh đi khi độ cao tăng lên (từ 7.000.000 °C tới khoảng 2.000.000 °C) làm gradient nhiệt độ này nhỏ hơn giá trị tỷ lệ khoảng đoạn nhiệt (adiabatic lapse rate) và vì thế không thể gây ra sự đối lưu.[32] Nhiệt được truyền bởi sự bức xạ—ion của hydro và heli phát ra các photon, nó chỉ di chuyển một khoảng cách ngắn trước khi bị tái hấp thụ bởi các ion khác.[40] Các photon thực tế bật lên rất nhiều lần xuyên qua vật chất đặc này tới mức một photon riêng lẻ mất khoảng một triệu năm để tới được lớp bề mặt, và vì thế, năng lượng chuyển ra ngoài rất chậm.[32] Mật độ giảm sút hàng trăm lần (từ 20 g/cm³ xuống chỉ 0,2 g/cm³) từ đáy lên đỉnh vùng bức xạ.[40]
Giữa vùng bức xạ và vùng đối lưu là một lớp chuyển tiếp được gọi là tachocline. Đây là vùng nơi có sự thay đổi mạnh giữa chuyển động xoay đồng tốc của vùng bức xạ và chuyển động chênh lệch của vùng đối lưu dẫn tới một sự trượt mạnh—một điều kiện nơi các lớp ngang giáp nhau trượt trên nhau.[41] Các dạng chuyển động giống chất lỏng trong vùng đối lưu bên trên, dần biến mất từ đỉnh của lớp này xuống đáy của nó, phù hợp với các đặc điểm yên tĩnh của vùng bức xạ trên đáy. Hiện tại, có giả thuyết cho rằng một nguồn phát điện từ bên trong lớp này tạo ra từ trường của Mặt Trời.[32]
Vùng đối lưu[sửa | sửa mã nguồn]
Trong lớp ngoài của Mặt Trời, từ bề mặt nó xuống xấp xỉ 200.000 km (hay 70% bán kính Mặt Trời), plasma Mặt Trời không đủ đặc hay đủ nóng để chuyển năng lượng nhiệt từ bên trong ra ngoài bằng bức xạ. Vì thế, đối lưu nhiệt diễn ra khi các cột nhiệt mang vật liệu nóng ra bề mặt (quyển sáng) của Mặt Trời. Khi vật liệu lạnh đi ở bề mặt, nó đi xuống dưới đáy vùng đối lưu, để nhận thêm nhiệt từ đỉnh vùng bức xạ. Ở bề mặt nhìn thấy được của Mặt Trời, nhiệt độ đã giảm xuống 5.700 K và mật độ chỉ còn 0,2 g/m³ (khoảng 1/10.000 mật độ không khí ở mực nước biển).[32]
Các cột nhiệt trong vùng đối lưu tạo nên một dấu vết trên Mặt Trời, dưới hình thức hột mặt trời (solar granulation) và siêu hột. Sự hỗn loạn đối lưu của bộ phận phía ngoài này của phần bên trong lòng Mặt Trời hình thành một máy phát điện "tỷ lệ nhỏ" xuất hiện tạo ra từ trường bắc và nam cực trên toàn bộ bề mặt Mặt Trời.[32] Các cột nhiệt của Mặt Trời là các pin Bénard và vì thế thường có hình lăng trụ năm cạnh.[42]
Quang quyển[sửa | sửa mã nguồn]
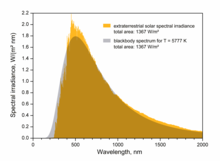
Nhiệt độ hiệu quả (effective temperature), hay nhiệt độ vật đen của Mặt Trời (5.777 K) là nhiệt độ của một vật thể đen với kích cỡ tương đương phải tạo ra cùng một tổng năng lượng bức xạ.
Bài chi tiết: Quang quyển Mặt Trời
Bề mặt nhìn thấy được của Mặt Trời hay quang quyển là lớp mà ở bên dưới nó, Mặt Trời trở nên mờ đục với ánh sáng nhìn thấy được.[43]Trên quang quyển ánh sáng khả kiến của Mặt Trời tự do đi vào không gian, và năng lượng của nó thoát hoàn toàn khỏi Mặt Trời. Sự thay đổi trong độ mờ đục xảy ra vì sự giảm số lượng ion H−, mà chúng dễ dàng hấp thụ ánh sáng.[43] Trái lại, ánh sáng khả kiến mà chúng ta nhìn thấy được tạo ra khi các electron phản ứng với các nguyên tử hydro để tạo ra các ion H−.[44][45] Quang quyển thực tế dày từ hàng chục tới hàng trăm kilômét, mờ hơn chút ít so với không khí trên Trái Đất. Bởi vì phần phía trên của quang quyển lạnh hơn phần phía dưới, hình ảnh Mặt Trời hiện lên sáng hơn ở trung tâm so với ở cạnh hay rìa của đĩa Mặt Trời, trong một hiện tượng được gọi là rìa tối (limb darkening).[43]Ánh sáng Mặt Trời có phổ gần giống với quang phổ vật đen cho thấy một nhiệt độ khoảng 6.000 K (các vùng sâu có nhiệt độ tới 6.400 K trong khi những vùng nông hơn là 4.400 K[40]), rải rác với các vạch hấp thụ nguyên tử từ các lớp loãng trên quang quyển. Quang quyển có mật độ hạt ~1023/m3 (khoảng 1% mật độ hạt của khí quyển Trái Đất ở mực nước biển).[40]
Những nghiên cứu ban đầu về phổ quang học của quang quyển, một số đường hấp thụ được tìm ra không tương ứng với bất kỳ một nguyên tố hoá học nào từng biết trên Trái Đất khi ấy. Năm 1868, Norman Lockyer đưa ra giả thuyết rằng các đường hấp thụ đó là bởi một nguyên tố mới mà ông gọi là "heli", theo tên thần Mặt Trời Hy Lạp Helios. Mãi 25 năm sau, heli mới được phân lập trên Trái Đất.[46]
Khí quyển[sửa | sửa mã nguồn]
Xem thêm: Vành nhật hoa và Vòng quầng (Coronal loop)

Trong một sự kiện nhật thực toàn phần, quầng mặt trời có thể quan sát được bằng mắt thường.
Các phần bên trên quang quyển của Mặt Trời được gọi chung là khí quyển Mặt Trời.[43] Chúng có thể được quan sát bằng kính viễn vọng trên toàn bộ dãy phổ điện từ, từ sóng radio qua ánh sáng nhìn thấy được tới tia gamma, và gồm năm vùng chính: nhiệt độ tối thiểu, sắc quyển, vùng chuyển tiếp, vành nhật hoa, và nhật quyển.[43] Nhật quyển, có thể được coi là khí quyển liên tục phía ngoài của Mặt Trời, mở rộng ra bên ngoài vượt quá cả quỹ đạo Sao Diêm Vương tới nhật mãn (heliopause), nơi nó hình thành một biên giới đường chấn động rõ rệt với không gian liên sao. Sắc quyển, vùng chuyển tiếp và vành nhật hoa nóng hơn nhiều so với bề mặt Mặt Trời.[43] Lý do giải thích việc này vẫn chưa rõ ràng, bằng chứng cho thấy rằng các sóng Alfvén có thể có đủ năng lượng để làm nóng vành nhật hoa.[47]
Hàn quyển[sửa | sửa mã nguồn]
Lớp lạnh nhất của Mặt Trời là vùng nhiệt độ tối thiểu nằm cách khoảng 500 km bên trên quanq quyển, với nhiệt độ cỡ 4.100 K.[43] Phần này của Mặt Trời đủ lạnh để tồn tại các phân tử như carbon monoxit và nước, có thể được phát hiện bởi quang phổ hấp thụ của chúng.[48]
Sắc quyển (chromosphere)[sửa | sửa mã nguồn]
Bên trên lớp nhiệt độ tối thiểu là một lớp dày khoảng 2.000 km, chủ yếu là quang phổ của các đường hấp thụ và phát xạ.[43] Nó được gọi là sắc quyển bắt nguồn từ từ chroma của Hy Lạp, có nghĩa màu sắc, bởi sắc quyển nhìn thấy được như một ánh sáng có màu ở đầu và cuối của các lần nhật thực toàn phần.[40] Nhiệt độ của sắc quyển tăng dần cùng với độ cao, lên khoảng 20.000 K ở gần đỉnh.[43] Ở phần phía trên của sắc quyển heli bị ion hoá một phần.[49]

Được Kính Viễn vọng Quang học Mặt Trời của Hinodechụp ngày 12 tháng 1 năm 2007, hình ảnh Mặt Trời này cho thấy tình trạng sợi nhỏ của plasma liên kết các vùng phân cực từ tính khác nhau.
Vùng chuyển tiếp[sửa | sửa mã nguồn]
Bên trên sắc quyển có một vùng chuyển tiếp mỏng (khoảng 200 km) trong đó nhiệt độ tăng nhanh từ khoảng 20.000 K ở thượng tầng sắc quyển lên tới nhiệt độ gần một triệu K tại miện.[50] Nhiệt độ gia tăng dễ dàng bởi sự ion hoá toàn bộ heli trong vùng chuyển tiếp, làm giảm mạnh sự bức xạ làm nguội của plasma.[49] Vùng chuyển tiếp không xảy ra ở một độ cao được xác định chính xác. Thực vậy, nó hình thành một kiểu quầng với các đặc tính kiểu sắc quyển như gai và sợi, và luôn chuyển động hỗn loạn.[40] Vùng chuyển tiếp không dễ được quan sát thấy từ bề mặt Trái Đất, mà thực tế chỉ có thể được quan sát thấy từ vũ trụ bằng các dụng cụ nhạy cảm với thành phần tử ngoại của quang phổ.[51]
Vành nhật hoa[sửa | sửa mã nguồn]
Vành nhật hoa kéo dài ra lớp khí quyển bên ngoài của Mặt Trời, nó có thể tích lớn hơn cả Mặt Trời. Vành nhật hoa liên tục mở rộng vào vũ trụ hình thành nên gió Mặt Trời, lấp đầy toàn bộ Hệ Mặt Trời.[52] Vành nhật hoa hạ, rất gần bề mặt Mặt Trời, có mật độ phân tử khoảng 1015–1016/m3.[49][Ghi chú 1] Nhiệt độ trung bình của vành nhật hoa và gió Mặt Trời khoảng 1–2 triệu kelvin, tuy nhiên, trong những vùng nóng nhất nó khoảng 8–20 triệu kelvin. Tuy chưa tồn tại 1 lý thuyết đầy đủ để tính nhiệt độ vành nhật hoa, ít nhất một số lượng nhiệt của nó được biết có từ sự tái liên thông từ trường.[52]
Nhật quyển[sửa | sửa mã nguồn]
Nhật quyển là khoảng trống xung quanh Mặt Trời, được lấp đầy bằng gió plasma Mặt Trời và kéo dài xấp xỉ khoảng 20 lần bán kính Mặt Trời (0,1 AU) ra các mép phía ngoài của Hệ Mặt Trời. Biên giới phía trong của nó được xác định là lớp mà tại đó dòng gió Mặt Trời trở nên superalfvénic — có nghĩa là nơi dòng chảy trở nên nhanh hơn tốc độ của sóng Alfvén.[53] Sự nhiễu loạn và các lực động lực học bên ngoài biên giới này không thể ảnh hưởng tới hình dạng của quầng Mặt Trời bên trong, bởi thông tin chỉ có thể di chuyển với tốc độ của các sóng Alfvén. Gió Mặt Trời đi ra bên ngoài liên tục xuyên qua Nhật quyển, hình thành nên trường điện từ Mặt Trời bên trong hình dạng xoắn ốc,[52] cho tới khi nó va chạm với nhật mãn với khoảng cách hơn 50 AU từ Mặt Trời. Tháng 12 năm 2004, tàu vũ trụ Voyager 1 đã vượt qua một dải chấn được cho là một phần của nhật mãn. Cả hai tàu Voyager đều ghi nhận mức độ hạt năng lượng cao khi chúng tiếp cận biên giới.
Từ trường[sửa | sửa mã nguồn]
Xem thêm: Từ trường của các sao

Dải dòng điện nhật quyển phát triển ra toàn hệ Mặt Trời, và tạo ra sự ảnh hưởng của từ trường quay của Mặt Trời lên plasma trong vật chất giữa các hành tinh.[54]
Mặt Trời là một sao có hoạt động của từ trường. Nó có từ trường biến đổi mạnh mẽ hàng năm và đổi hướng sau mỗi 11 năm.[55] Từ trường của Mặt Trời tăng lên gây ra một số hiệu ứng gọi chung là hoạt động của Mặt Trời bao gồm vết đen trên bề mặt của Mặt Trời, vết sáng Mặt Trời, và các bức xạ trong gió Mặt Trời, chúng mang vật chất vào trong hệ Mặt Trời.[56] Các ảnh hưởng của hoạt động bức xạ này lên Trái Đất như cực quang ở các vĩ độ trung bình đến cao, và sự gián đoạn việc truyền sóng radio và điện năng. Hoạt động của Mặt Trời được cho là có vai trò quan rất lớn trong sự hình thành và tiến hóa của hệ Mặt Trời và làm thay đổi cấu trúc tầng điện ly của Trái Đất.[57]
Tất cả vật chất trong Mặt Trời đều ở thể khí và plasma do có nhiệt độ cao. Điều này có thể làm cho vận tốc quay ở vùng xích đạo (khoảng 25 ngày) nhanh hơn ở các vùng có vĩ độ cao hơn (khoảng 35 ngày ở gần các cực). Vận tốc quay khác nhau ở các vĩ độ của Mặt Trời tạo ra các đường sức từ xoắn vào nhau theo thời gian, tạo ra các vòng hoa từ tường phun ra từ bề mặt của Mặt Trời và tạo ra các vết đen Mặt Trời và các tai lửa Mặt Trời (xem sự nối lại từ trường). Sự xoắn vào nhau này làm tăng quá trình phát sinh từ trường của Mặt Trời và gây ra sự đảo từ của Mặt Trời theo chu kỳ 11 năm.[58][59]
Từ trường của Mặt Trời mở rộng ra ngoài ranh giới của nó. Plasma trong gió Mặt Trời bị từ hóa mang từ trường của Mặt Trời vào không gian tạo ra từ trường giữa các hành tinh.[52] Vì plasma chỉ có thể chuyển động trên các đường sức từ, từ trường giữa các hành tinh được mở rộng xuyên tâm từ Mặt Trời ra ngoài không gian. Do trường từ ở trên và dưới xích đạo khác nhau về cực hướng vào và hướng ra khỏi Mặt Trời, nên tồn tại một lớp dòng điện mỏng trên mặt phẳng xích đạo được gọi là dải dòng điện nhật quyển (heliospheric current sheet).[52] Ở khoảng cách lớn, sự quay của Mặt Trời xoắn từ trường và dải dòng này thành cấu trúc giống xoắn ốc Archimedes gọi là xoắn ốc Parker.[52] Từ trường giữa các hành tinh mạnh hơn từ trường ở hai cực của Mặt Trời. Từ trường ở hai cực của Mặt Trời 50–400 μT (trong Quang quyển) giảm theo hàm mũ bậc ba của khoảng cách và đạt 0,1 nT ở Trái Đất. Tuy nhiên, theo các thăm dò từ tàu không gian cho thấy từ trường giữa các hành tinh ở vị trí của Trái Đất cao hơn khoảng 100 lần so với con số trên, vào khoảng 5 nT.[60]
Thành phần hóa học[sửa | sửa mã nguồn]
Mặt Trời được cấu tạo chủ yếu bởi các nguyên tố hydro và heli, các nguyên tố này chiếm tương ứng 74,9% và 23,8% khối lượng của Mặt Trời trong quang quyển.[61] Các nguyên tố nặng hơn được gọi là kim loại trong thiên văn học, chiếm ít hơn 2% khối lượng Mặt Trời. Trong đó phổ biến nhất là oxy (chiếm gần 1% khối lượng Mặt Trời), cacbon (0,3%), neon (0,2%), và sắt (0,2%).[62]
Thành phần hóa học của Mặt Trời thừa hưởng các nguyên tố từ vật chất giữa các sao khi nó hình thành: hydro và heli trong Mặt Trời được tạo ra từ tổng hợp hạt nhân Big Bang. Các kim loại này được tạo ra bởi tổng hợp hạt nhân sao khi kết thúc quá trình tiến hóa sao và trả các vật liệu của chúng về khoảng không giữa các sao trước khi Mặt Trời hình thành.[63] Thành phần hóa học của quang quyển thường được xem là đại diện cho các thành phần của hệ Mặt Trời nguyên thủy.[64] Tuy nhiên, khi Mặt Trời hình thành, heli và các nguyên tố nặng tích tụ trong quang quyển. Do đó, quang quyển ngày nay chứa ít heli và chỉ có khoảng 84% các nguyên tố nặng so với sao tổ tiên; sao tổ tiên có 71,1% hydro, 27,4% heli, và 1,5% kim loại.[61]
Bên trong Mặt Trời, các phản ứng tổng hợp hạt nhân làm biến đổi thành phần của nó do hidro biến thành heli - phản ứng nhiệt hạch, vì vậy phần trong cùng nhất của Mặt Trời hiện tại chỉ có khoảng 60% heli, còn hàm lượng kim loại phổ biến thì không đổi. Do phần bên trong Mặt Trời có hoạt động phóng xạ, chứ không phải đối lưu (xem cấu trúc ở trên), nên không có sản phẩm tổng hợp hạt nhân nào từ lõi đi vào quang quyển.[65]
Các nguyên tố nặng phổ biến trong Mặt Trời mô tả bên trên được đo đạc đồng thời bằng quang phổ trong quang quyển và bằng các vật chất trong thiên thạch không bị nung chảy. Các thiên thạch này được cho là có chứa thành phần của ngôi sao tiền Mặt Trời và không bị ảnh hưởng bởi sự tích tụ các nguyên tố nặng. Đó là hai cách đo đạc được nhiều người đồng ý nhất.[9]
Các nguyên tố nhóm sắt bị ion hóa[sửa | sửa mã nguồn]
Trong thập niên 1970, nhiều nghiên cứu tập trung vào sự phong phú của các nguyên tố nhóm sắt trong Mặt Trời.[66][67] Mặc dù các nghiên cứu này mang lại nhiều ý nghĩa, nhưng việc xác định sự phong phú của các nguyên tố nhóm sắt (như coban và mangan) vẫn còn là khó khăn vào thời điểm đó do các cấu trúc siêu mịn của chúng.[66]
Một bộ hoàn chỉnh về độ mạnh dao động đầu tiên của các nguyên tố nhóm sắt bị ion hóa riêng lẻ được thực hiện thành công vào thập niên 1960,[68] và được nâng cấp vào năm 1976.[69] Năm 1978, sự phong phú về các nguyên tố thuộc nhóm sắt bị ion hóa đã được nhận dạng.[66]
Quan hệ sự phân tầng khối lượng giữa hành tinh và Mặt Trời[sửa | sửa mã nguồn]
Nhiều tác giả khác nhau đề cập đến sự tồn tại của mối quan hệ phân tầng khối lượng giữa các thành phần đồng vị của Mặt Trời và khí trơ trên các hành tinh,[70] ví dụ như sự tương quan giữa thành phần đồng vị của hành tinh và Mặt Trời là Ne và Xe.[71] Tuy nhiên, người ta tin rằng toàn bộ Mặt Trời có cùng thành phần như nhau trong khi bầu khí quyển của Mặt Trời vẫn trải rộng và ít nhất là đến năm 1983.[72] Năm 1983, người ta cho rằng có sự phân tầng trên Mặt Trời, chính vì vậy đã tạo ra mối quan hệ phân tầng giữa các thành phần đồng vị của hành tinh và gió Mặt Trời là các khí hiếm.[72]
Các chu kỳ trên Mặt Trời[sửa | sửa mã nguồn]
Các vết đen Mặt Trời[sửa | sửa mã nguồn]
Bài chi tiết: Vết đen Mặt Trời

Số liệu đo đạc chu kỳ mặt trời thay đổi trong vòng 30 năm gần đây
Khi quan sát Mặt Trời bằng các bộ lọc thích hợp, các đặc điểm dễ nhận ra ngay đó là các vết đen Mặt Trời, chúng là các khu vực bề mặt được xác định rõ ràng bởi vì chúng tối hơn các khu vực xung quanh do nhiệt độ của chúng thấp hơn. Các vết đen này là những vùng có hoạt động từ trường mạnh, ở đây sự đối lưu được điều khiển bởi các trường từ mạnh, nhằm giải phóng năng lượng từ bên trong Mặt Trời lên bề mặt của nó. Trường từ làm nóng phần lõi, tạo thành các vùng hoạt động đây chính là nguồn gây ra vết lóa Mặt Trời (solar flare) và phóng thích vật chất vành nhật hoa (CME). Các vết đen lớn nhất có thể vươn xa hàng chục ngàn km.[73]
Số lượng các vết đen có thể thấy được trên Mặt Trời thì không cố định, nhưng chúng thay đổi theo chù kỳ 11 năm hay còn gọi là chu kỳ Mặt Trời. Trong điều kiện bình thường, chỉ có vài vết đen có thể quan sát được, và hiếm khi quan sát được hết tất cả. Một số xuất hiện ở các vĩ độ lớn hơn. Khi diễn ra chu kỳ Mặt Trời, số lượng các vết đen tăng và chúng di chuyển gần hơn về phía xích đạo của Mặt Trời, hiện tượng này được miêu tả trong quy luật Spörer. Các vết đen luôn tồn tại thành cặp có cực từ đối nhau. Cực từ của vết đen xen kẽ mỗi chu kỳ Mặt Trời, vì thế nó sẽ là cực bắc từ trong một chu kỳ và sẽ là cực nam trong chu kỳ tiếp theo.[74]

Lịch sử quan sát các vết đen mặt trời trong vòng 250 năm gần đây, cho thấy chu kỳ mặt trời khoảng ~11 năm
Chu kỳ Mặt Trời có ảnh hưởng lớn đến thời tiết không gian, và cũng như khí hậu trên Trái Đất do độ sáng có mối quan hệ trực tiếp với hoạt động từ trường.[75] Cực tiểu hoạt động của Mặt Trời có xu hướng tương quan với nhiệt độ lạnh hơn, và lâu hơn so với các chu kỳ mặt trời trung bình có xu hướng tương quan đến nhiệt độ nóng hơn. Trong thế kỷ XVII, chu kỳ mặt trời dường như đã ngưng hoàn toàn trong vài thập kỷ; có rất ít vết đen được quan sát trong giai đoạn này. Cũng trong giai đoạn này, hay còn gọi là cực tiểu Maunder hay thời kỳ băng hà nhỏ, châu Âu đã trải qua thời kỳ nhiệt độ rất lạnh.[76] Hoạt động cực tiểu vào thời kỳ trước đây được phát hiện thông qua việc phân tích vòng sinh trưởng của cây đã sinh sống vào thời gian nhiệt độ toàn cầu thấp hơn nhiệt độ trung bình.[77]
Chu kỳ dài[sửa | sửa mã nguồn]
Một giả thuyết gần đây nêu rằng từ trường không ổn định trong lõi của Mặt Trời tạo ra sự dao động với chu kỳ 41.000 hoặc 100.000 năm. Điều này có thể cung cấp các dữ kiện để giải thích về thời kỳ băng hà hơn là chu kỳ Milankovitch.[78][79]
Vị trí và chuyển động trong dải Ngân Hà[sửa | sửa mã nguồn]

Sự chuyển động của tâm tỉ cự của hệ Mặt Trời tương đối với Mặt Trời.

Geminga, phía trên bên trái và sao xung Con Cua.
Ảnh chụp trong phổ tia gamma
Sự chuyển động của Mặt Trời liên quan đến khối tâm của hệ Mặt Trời trở nên phức tạp do các nhiễu loạn từ các hành tinh. Cứ mỗi vài trăm năm chuyển động này lại thay đổi giữa cùng hướng và ngược hướng với các thiên thể khác.[80] Mặt Trời nằm gần rìa trong của nhánh Orion của Ngân Hà, trong đám mây liên sao Địa phương hoặc vành đai Gould, với khoảng cách giả thuyết 7,5–8,5 kpc (25.000–28.000 năm ánh sáng) tính từ tâm Ngân Hà,[81][82][83][84] nằm bên trong Bong bóng địa phương, một không gian khí nóng loãng, có thể được tạo ra từ phần còn sót lại của siêu tân tinh, Geminga, một nguồn phát xạ tia gamma sáng chói.[85] Khoảng cách giữa nhánh địa phương và nhánh gần đó là nhánh Perseusvào khoảng 6.500 năm ánh sáng.[86]
Điểm apec của đường đi của Mặt Trời là hướng mà mặt trời đi qua không gian của thiên hà. Hướng chung của chuyển động của Mặt Trời thẳng về sao Vega gần chòm sao Hercules, với góc gần 60 độ khối (sky degree) so với hướng của tâm Ngân Hà. Nếu một người nào đó quan sát Mặt Trời từ Alpha Centauri, hệ sao gần nhất, Mặt Trời sẽ xuất hiện trong chòm sao Cassiopeia.[87]
Quỹ đạo của Mặt Trời xung quanh Ngân Hà được cho là dạng elip có một chút nhiễu do các nhánh xoắn ốc và sự phân bố khối lượng không đồng nhất của thiên hà. Thêm vào đó, Mặt Trời dao động lên và xuống so với mặt phẳng thiên hà khoảng 2,7 lần trong một quỹ đạo. Đều này tương tự với một dao động điều hòa đơn giản không có lực kéo nào. Đã từng có tranh luận rằng sự chuyển động của Mặt Trời xuyên qua các nhánh xoắn ốc mật độ cao hơn đôi khi bằng với các sự kiện tuyệt chủng lớn trên Trái Đất, có lẽ là do làm tăng các sự kiện va chạm (impact event).[88] Hệ Mặt Trời mất khoảng 225–250 triệu năm để hoàn thiện một vòng quỹ đạo của nó trong Ngân Hà (hay một năm ngân hà),[89] vì vậy, tổng số vòng quay của Mặt Trời quanh Ngân Hà là khoảng 20–25 trong cuộc đời đã qua của nó. Vận tốc quỹ đạo của hệ Mặt Trời so với tâm của Ngân Hà vào khoảng 251 km/s.[19] Với vận tốc này, nó mất khoảng 1.400 năm để hệ Mặt Trời đi được một khoảng cách của 1 năm ánh sáng, hay 8 ngày để đi được 1 AU.[90]
Các vấn đề về các học thuyết[sửa | sửa mã nguồn]
Neutrino Mặt Trời[sửa | sửa mã nguồn]
Trong một vài năm số lượng neutrino electron Mặt Trời được phát hiện trên Trái Đất từ 1⁄3 đến 1⁄2 so với số lượng dự đoán bằng Mô hình chuẩn của Mặt Trời. Kết quả bất thường này được đặt tên là vấn đề neutrino Mặt Trời. Các giả thuyết đưa ra để giải quyết vấn đề này hoặc là sự giảm nhiệt độ bên trong Mặt Trời làm cho dòng nơtrino thấp hơn, hoặc là khẳng định rằng các nơtrino electron có thể dao động liên quan đến các neutrino tau và neutrino muon, mà hai loại này không thể nhận biết được khi chúng chuyển động giữa Mặt Trời và Trái Đất.[91] Một vài quan sát về nơtrino đã bắt đầu thực hiện trong thập niên 1980 để đo dòng nơtrino Mặt Trời với độ chính xác có thể, bao gồm Đài quan sát Neutrino Sudbury và Kamiokande.[92] Các kết quả cho thấy các nơtrinos có khối lượng tĩnh rất nhỏ và thực tế là có sự dao động.[93][39] Ngoài ra, vào năm 2001 dự án Đài quan sát Neutrino Sudbury đã có thể nhận dạng ba loại nơtrino một cách trực tiếp, và thấy rằng tốc độ phát xạ tổng số các nơtrino của Mặt Trời phù hợp với Mô hình chuẩn Mặt Trời, mặc dù nó phụ thuộc vào năng lượng nơtrino làm cho có 1/3 nơtrino được phát hiện trên Trái Đất là loại nơtrino electron.[92][94] Tỷ lệ này phù hợp với dự đoán theo hiệu ứng Mikheyev-Smirnov-Wolfenstein (hay còn gọi là hiệu ứng vật chất). Hiệu ứng này miêu tả sự dao động của vật chất, và nó được xem là một lời giải cho vấn đề này.[92]
Nhiệt độ vành nhật hoa[sửa | sửa mã nguồn]
Bài chi tiết: Vành nhật hoa
Nhiệt độ bề mặt Mặt Trời (quang quyển) vào khoảng 6.000 K. Bên trên nó là vành nhật hoa, nhiệt độ lên đến 1 - 2 triệu K.[50] Nhiệt độ của vành nhật hoa cao cho thấy rằng nó đã bị nung nóng bởi một cơ chế nào đó khác với sự đối lưu nhiệt trực tiếp từ quang quyển.[52]
Người ta cho rằng năng lượng cần thiết để làm nóng vành nhật hoa được cung cấp bởi sự chuyển động hỗn loạn trong đới đối lưu nằm dưới quang quyển, và có hai cơ chế chính đã được đề xuất để giải thích về nhiệt độ cao của vành nhật hoa.[50]
- Thứ nhất là nung nóng bằng sóng, các sóng từ thủy động hoặc trọng lực được tạo ra bởi sự rối trong đới đối lưu.[50] Các sóng này chuyển động hướng lên và bị tán xạ vào vành nhật hoa, tích tụ năng lượng của chúng trong lớp không khí xung quanh ở dạng nhiệt.[95]
- Thứ hai là nung nóng bởi từ trường, theo đó năng lượng từ được hình thành một cách liên tục bởi sự chuyển động của quang quyển và được giải phóng thông qua tái liên kết từ trường ở dạng các vết sáng Mặt Trời lớn và vô số các dạng tương tự với kích thước nhỏ hơn.[96]
Hiện tại, chưa có câu trả lời rõ ràng rằng có phải các sóng ảnh hưởng đến cơ chế nung nóng này hay không. Tất cả các sóng trừ sóng Alfvén đã được phát hiện là tán xạ hoặc phản xạ trước khi chúng chạm đến vành nhật hoa.[97] Thêm vào đó, các sóng Alfvén không dễ dàng tán xạ vào vành nhật hoa. Các nghiên cứu hiện tại tập trung theo hướng cơ chế nung nóng bởi các vết sáng mặt trời.[50]
Sao trẻ[sửa | sửa mã nguồn]
Bài chi tiết: Nghịch lý Mặt Trời trẻ
Các mô hình lý thuyết về sự phát triển của Mặt Trời cho rằng cách đây khoảng 3,8 đến 2,5 tỉ năm, vào liên đại Thái Cổ, Mặt Trời chỉ sáng bằng khoảng 75% so với hiện nay. Như một ngôi sao yếu nó không thể duy trì lượng nước ổn định trên bề Mặt Trái Đất, và sự sống đã có thể không phát triển. Tuy nhiên, các chứng cứ địa chất chứng minh rằng Trái Đất đã trải qua ở chế độ nhiệt độ tương đối ổn định trong suốt thời kỳ lịch sử của nó, và rằng Trái Đất trẻ vào thời điểm nào đó trong quá khứ đã ấm hơn hiện nay. Các cuộc tranh luận giữa các nhà khoa học rằng khí quyển của Trái Đất trẻ chứa nhiều khí nhà kính (như carbon dioxit, metan và amoniac) hơn hiện tại, các khí này giữ nhiệt đủ để làm cân bằng nhiệt độ Trái Đất từ một lượng nhỏ năng lượng mặt trời đi đến Trái Đất.[98]
Các dị thường hiện tại[sửa | sửa mã nguồn]
Mặt Trời hiện tại đang thể hiện những bất thường theo nhiều cách.[99][100]
- Nó đang trong giai đoạn giữa của thời kỳ ít vết đen mặt trời bất thường, thời kỳ này kéo dài hơn và tỷ lệ các ngày không có vết đen cao hơn bình thường; từ tháng 5 năm 2008, các dự đoán về sự tăng cường hoạt động của vết đen sắp xảy ra đã bị phủ nhận.
- Có thể đo đạc được độ mờ; lượng phát xạ giảm 0,02% ở các bước sóng khả kiến và 6% ở các bước sóng EUV so với các mức ở thời kỳ tối thiểu vết đen gần nhất.[101]
- Qua hai thập kỷ gần đây, vận tốc gió mặt trời giảm 3%, nhiệt độ giảm 13%, và mật độ giảm 20%.[102]
- Cường độ từ trường mặt trời giảm phân nửa so với thời kỳ thấp nhất cách đây 22 năm. Toàn bộ nhật quyển lấp đầy trong hệ Mặt Trời đã bị co lại, làm tăng độ bức xạ vũ trụ lên khí quyển Trái Đất.
Thám hiểm Mặt Trời[sửa | sửa mã nguồn]
Những hiểu biết trước đây[sửa | sửa mã nguồn]

Thần Mặt Trời Helios cưỡi xe ngựa Chariot trong hình dung của người Hy Lạp cổ đại
Tranh của Johann Baptist thế kỷ XVIII
Hiểu biết cơ bản nhất của nhân loại về Mặt Trời đó là một đĩa sáng trong bầu trời, khi nó xuất hiện thì gọi là ban ngày, còn khi nó biến mất là ban đêm. Trong các nền văn hóa cổ đại và tiền sử, Mặt Trời được xem là thần Mặt Trời hay các hiện tượng siêu nhiên khác. Thờ cúng Mặt Trời là tâm điểm của các nền văn minh như Inca ở Nam Mỹ và Aztec thuộc México ngày nay. Một số tượng đài cổ được xây dựng với ý tưởng kết hợp với các hiện tượng liên quan đến Mặt Trời; ví dụ, các cự thạch đánh dấu một cách chính xác đông chí hoặc hạ chí (các cự thạch nổi tiếng phân bố ở Nabta Playa, Ai Cập, Mnajdra, Malta và ở Stonehenge, Anh). Vào thời kỳ La Mã, ngày sinh của Mặt Trời là ngày nghỉ để kỉ niệm Sol Invictus chỉ sau đông chí mà ngày nay gọi là Christmas. Dựa theo các sao cố định, Mặt Trời xuất hiện từ Trái Đất xoay một lần mất một năm theo mặt phẳng hoàng đạo xuyên qua mười hai chòm sao, và vì thế các nhà thiên văn học Hy Lạp cho rằng nó là một trong 7 hành tinh (Hy Lạp planetes nghĩa là "đi lang thang"), sau đó nó được đặt tên cho 7 ngày trong tuần trong một số ngôn ngữ.[103][104][105]
Sư hiểu biết cùng với tiến bộ khoa học[sửa | sửa mã nguồn]
Trước Công nguyên[sửa | sửa mã nguồn]
Vào đầu thiên niên kỷ 1 TCN, các nhà thiên văn học Babylon đã quan sát thấy rằng sự chuyển động của Mặt Trời theo đường hoàng đạo là không đồng nhất, mặc dù họ không biết tại sao như thế; với kiến thức ngày nay thì đó là do Trái Đất chuyển động theo quỹ đạo elip quanh Mặt Trời, khi đó Trái Đất sẽ chuyển động nhanh hơn khi nó ở gần Mặt Trời tại điểm cận nhật và chậm hơn khi nó ở xa điểm viễn nhật.[106]

Anaxagoras
Một trong những người tiên phong nêu ra lời giải thích khoa học về Mặt Trời là nhà triết học Hy Lạp Anaxagoras (500-428 TCN). Ông cho rằng Mặt Trời là quả cầu lửa kim loại khổng lồ, thậm chí lớn hơn Peloponnesus, và không phải là xe ngựa chariot của thần Mặt Trời Helios.[107] Khi giảng về vấn đề dị giáo này, ông đã bị bỏ tù bởi nhà cầm quyền và bị tuyên án tử hình, mặc dù sau đó ông được phóng thích bởi sự can thiệp của Pericles. Sau đó hai thế kỷ, vào thế kỷ III TCN nhà toán học, thi sĩ, thiên văn học Hy Lạp Eratosthenes đã ước tính khoảng cách giữa Trái Đất và Mặt Trời vào khoảng "400 vạn và 80.0000 thước đo tầm xa (stadia)", việc giải nghĩa vẫn chưa rõ ràng, nó ám chỉ hoặc 4.080.000 stadia (755.000 km) hoặc 804.000.000 stadia (148 đến 153 triệu km); con số sau là chính xác với sai số vài phần trăm.
Công nguyên[sửa | sửa mã nguồn]
Vào thế kỷ I, nhà toán học, thiên văn học xứ Alexandria Ptolemy đã ước tính khoảng cách này gấp 1.210 lần bán kính Trái Đất.[108] Vào thế kỷ VIII, nhà toán học, thiên văn học người Ba Tư Yaqūb ibn Tāriq đã ước tính khoảng cách giữa Trái Đất và Mặt Trời gấp 8.000 lần bán kính Trái Đất, một con số lớn nhất về đơn vị thiên văn cho đến thời điểm đó.[109]
Những đóng góp cho thiên văn học của người Ả rập như Albatenius phát hiện rằng hướng độ lệch tâm của Mặt Trời đang thay đổi,[110] và Ibn Yunus quan sát hơn 10.000 vị trí của Mặt Trời trong nhiều năm bằng thiết bị đo độ cao thiên thể.[111] Sự chuyển động của Sao Kim được Avicenna quan sát đầu tiên vào năm 1032 và ông kết luận rằng Sao Kim nằm gần Trái Đất hơn Mặt Trời,[112] còn quan sát đầu tiên về sự chuyển động của Sao Thủy do Ibn Bajjah thực hiện vào thế kỷ XII.[113] Nhà vật lý Ả rập, Alhazen, đã nghiên cứu các đặc điểm của ánh sáng Mặt Trời bằng các thí nghiệm với camera trong buồng tối obscura, được miêu tả trong quyển Sách quang học (1021), và đã minh họa rằng Mặt Trời là nguồn cung cấp ánh sáng cho Mặt Trăng.[114] Để tạo nên công trình của ông vào thế kỷ XIII, Qutb al-Din al-Shirazi và Theodoric của Freiberg đã đưa ra các giải thích chính xác về hiện tượng cầu vồng, còn Kamāl al-Dīn al-Fārisī đã xác nhận thông qua các thí nghiệm bằng camera obscura rằng màu sắc của hiện tượng cầu vồng là sự phân tán của ánh sáng Mặt Trời.[115][116][117][118] Trong thế kỷ XIII, nhà thiên văn học đạo Hồi Maghribi đã ước tính đường kính Mặt Trời khoảng 255 lần đường kính Trái Đất,[119] con số này lớn gấp đôi con số hiện tại được chấp nhận.
Thuyết nhật tâm[sửa | sửa mã nguồn]
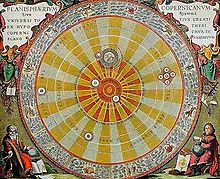
Mô hình hệ mặt trời với mặt trời ở tâm của Copernicus
Giả thuyết rằng Mặt Trời là trung tâm của quỹ đạo chuyển động của các hành tinh được Aristarchus của Samos (310-230 TCN) đưa ra vào thế kỷ III TCN, và sau đó Seleucus của Seleucia cũng theo thuyết này (xem thuyết Nhật tâm). Quan điểm triết học quan trọng này đã được phát triển thành mô hình toán học dự đoán một cách hoàn chỉnh về hệ nhật tâm vào thế kỷ XVI bởi Nicolaus Copernicus. Vào đầu thế kỷ XVII, việc phát minh ra kính viễn vọng đã cho phép các quan sát chi tiết hơn về vết đen Mặt Trời do Thomas Harriot, Galileo Galilei và các nhà thiên văn khác thực hiện. Galileo đã thực hiện một số quan sát vết đen Mặt Trời bằng kính viễn vọng và thừa nhận rằng chúng nằm trên bề mặt của Mặt Trời hơn là các vật thể nhỏ chuyển động qua khoảng không giữa Trái Đất và Mặt Trời.[120] Các vết đen Mặt Trời cũng được các nhà thiên văn Trung Quốc quan sát vào thời nhà Hán (206 TCN - 220 CN), họ đã duy trì ghi chép các quan sát này trong vài thế kỷ. Averroes cũng đưa ra một miêu tả về các vết đen Mặt Trời trong thế kỷ XII.[121]
Năm 1672 Giovanni Cassini và Jean Richer xác định được khoảng cách đến Sao Hỏa và đã tính được khoảng cách đến Mặt Trời. Isaac Newton quan sát ánh sáng Mặt Trời bằng lăng kính, và thấy nó được tạo thành từ nhiều màu sắc,[122] trong khi đó vào năm 1800 William Herschel phát hiện ra bức xạ hồng ngoại nằm gần ánh sáng đỏ trong quang phổ của Mặt Trời.[123] Thập niên 1800 phát triển mạnh các kính quang phổ nghiên cứu về Mặt Trời, và Joseph von Fraunhofer đã thực hiện các quan sát đầu tiên về các vạch hấp thụ quang phổ, vạch mạnh nhất vẫn thường được gọi theo tên của ông là vạch Fraunhofer. Khi mở rộng dải quang phổ của sánh sáng từ Mặt Trời thì có một số màu bị mất được phát hiện.
Thiên văn học hiện đại[sửa | sửa mã nguồn]
Vào những năm đầu tiên của kỷ nguyên khoa học hiện đại, nguồn năng lượng Mặt Trời vẫn là vấn đề còn nhiều bí ẩn. Lord Kelvin đã đề nghị rằng Mặt Trời là một vật thể lỏng đang lạnh đi một cách từ từ vì vậy nó đang phát ra nhiệt dự trữ bên trong lòng nó.[124] Sau đó, Kelvin và Hermann von Helmholtz đưa ra cơ chế Kelvin-Helmholtz để giải thích lượng năng lượng tỏa ra này. Tuy nhiên, kết quả tính tuổi Mặt Trời chỉ có 20 triệu năm, một con số rất nhỏ so với các tính toán mà các dấu hiệu địa chất lúc đó đưa ra là ít nhất 300 triệu năm.[124] Năm 1890 Joseph Lockyer, người đã phát hiện ra heli trong quang phổ của Mặt Trời, đã đưa ra giả thuyết thiên thạch về sự hình thành và tiến hóa của Mặt Trời.[125]
Mãi cho đến năm 1904 thì vấn đề này mới được giải quyết. Ernest Rutherford cho rằng lượng bức xạ Mặt Trời có thể đã được duy trì bởi một nguồn nhiệt bên trong nó, và đó là hoạt động phân rã phóng xạ.[126] Tuy nhiên, Albert Einstein là người đã đưa ra mối quan hệ giữa nguồn năng lượng phát ra từ Mặt Trời với phương trình cân bằng khối lượng-năng lượng E = mc2.[127]
Năm 1920, Sir Arthur Eddington đề xuất rằng áp suất và nhiệt động trong lõi của Mặt Trời có thể phát sinh một phản ứng hợp hạch hạt nhân theo đó các hạt nhân hidro (proton) hợp lại tạo ra hạt nhân heli, quá trình này sinh ra năng lượng đồng thời sẽ làm giảm dần khối lượng.[128] Lượng hdro chiếm ưu thế trong Mặt Trời được Cecilia Payne xác nhận vào năm 1925. Quan điểm lý thuyết về tổng hợp hạt nhân được các nhà vật lý thiên văn Subrahmanyan Chandrasekhar và Hans Bethe phát triển vào thập niên 1930. Hans Bethe đã tính toán chi tiết hai phản ứng sinh năng lượng chính trên Mặt Trời.[129][130]
Sau cùng, một bài báo có ảnh hưởng lớn của Margaret Burbidge được xuất bản năm 1957 với tựa là "Sự tổng hợp các nguyên tố của các Sao" ("Synthesis of the Elements in Stars").[131] Bài báo đã minh hoạ một cách thuyết phục rằng hầu hết các nguyên tố trong vũ trụ đã và đang được tổng hợp bằng các phản ứng hạt nhân bên trong các ngôi sao, giống như Mặt Trời.
Các nhiệm vụ khám phá không gian[sửa | sửa mã nguồn]
 | Wikimedia Commons có thư viện hình ảnh và phương tiện truyền tải về Tàu SOHO |
 | Wikimedia Commons có thư viện hình ảnh và phương tiện truyền tải về Tàu Genesis |

Hình ảnh Mặt Trăng đi ngang qua Mặt Trời nhìn từ tàu STEREO-B ngày 25 tháng 2 năm 2007. Do STEREO-B cũng di chuyển quanh Mặt Trời theo quỹ đạo Trái Đất và có khoảng cách đến Mặt Trăng xa hơn so với khoảng cách từ Trái Đất, Mặt Trăng trông nhỏ hơn so với Mặt Trời [132]
Các vệ tinh đầu tiên được thiết kế để giám sát Mặt Trời là Pioneer 5, 6, 7, 8 và 9 của NASA, được phóng lên trong khoảng 1959 - 1968. Các vệ tinh mang máy dò này quay quanh Mặt Trời với khoảng cách tương tự như vệ tinh bay quanh Trái Đất, và thực hiện các đo đạc chi tiết đầu tiên về gió Mặt Trời và trường từ Mặt Trời. Pioneer 9 vận hành trong thời gian tương đối dài và truyền dữ liệu về đến năm 1987.[133]
Trong thập niên 1970, hai phi thuyền Helios và Skylab cùng với kính thiên văn Apollo cung cấp cho các nhà khoa học những dữ liệu mới về gió Mặt Trời và vành nhật hoa. Hai bộ phận thăm dò Helios 1 and 2 kết hợp giữa Hoa Kỳ và Đức cùng nghiên cứu gió Mặt Trời bay trong quỹ đạo của Sao Thủy ở điểm cận nhật.[134] Trạm không gian Skylab được NASA phóng năm 1973 gồm các mô-đun quan sát Mặt Trời gọi là Apollo Telescope Mount, mô-đun này được vận hành bởi các nhà du hành vũ trụ định cư trên đó.[51] Skylab đã thực hiện các quan sát thời gian đầu tiên về các cùng Mặt Trời chuyển động qua và sự phát xạ tia tử ngoại từ vành nhật hoa.[51] Các phát hiện bao gồm các giám sát đầu tiên về sự phát xạ vật chất vành nhật hoa, còn gọi là "coronal transients", và các hố nhật hoa, ngày nay cho thấy rằng nó liên quan đến gió Mặt Trời.[134]
Năm 1980, phi vụ Solar Maximum Mission được phóng bởi NASA. Phi thuyền này được thiết kế để giám sát các tia gamma, tia X và UV từ các vết lóa Mặt Trời trong suốt thời gian hoạt động của Mặt Trời mạnh và độ sáng Mặt Trời. Tuy nhiên, chỉ một vài tháng sau khi phóng, một sự cố về điện làm cho đầu dò chuyển sang chế độ dự phòng, và phải mất 3 tháng hoạt động ở chế độ này. Năm 1984 nhiệm vụ Space Shuttle Challenger STS-41 đã khôi phục vệ tinh và sửa hệ thống điện trước khi đưa nó trở vào quỹ đạo. Solar Maximum Mission đã cung cấp hàng ngàn tấm ảnh về vành nhật hoa trước khi trở về khí quyển Trái Đất tháng 6 năm 1989.[135]
Một trong những chương trình mang nhiệm vụ quan trọng là phóng "Đài quan sát Mặt Trời và nhật quyển" (SOHO-Solar and Heliospheric Observatory) vào ngày 2 tháng 12 năm 1995 do Cơ quan Vũ trụ châu Âu (ESA) và Cục Quản trị Hàng không và Không gian Quốc gia Hoa Kỳ (NASA) hợp tác.[51] Soho nằm tại một điểm khá đặc biệt trong không gian, điểm Lagrange L1. Điểm Lagrange là điểm nằm giữa Trái Đất và mặt trời, cách Trái Đất chừng 1,6 triệu km, nơi có điểm trọng lực cân bằng giữa các hành tinh.
Sự giàu có của các nguyên tố trong quang quyển được biết rất rõ từ các nghiên cứu quang phổ thiên văn, nhưng thành phần bên trong Mặt Trời thì được biết ít hơn. Tàu Genesis, được thiết kế để lấy mẫu gió Mặt Trời, cho phép các nhà thiên văn có thể trực tiếp đo đạc thành phần vật chất của Mặt Trời. Nó trở lại Trái Đất năm 2004 và lẽ ra sẽ được phân tích, nhưng nó đã bị hư hại nặng khi hạ cánh do dù không mở khi đi vào bầu khí quyển của Trái Đất.[136][137]
| [hiện] Các chương trình thám hiểm Mặt Trời |
|---|
|
Mặt Trời là nguồn năng lượng khổng lồ[sửa | sửa mã nguồn]

Mặt Trời là ngôi sao gần Trái Đất nhất - Hình chụp mặt trời dưới ánh sáng nhìn thấy được
Bài chi tiết: Năng lượng Mặt Trời
Ánh sáng nói riêng, hay bức xạ điện từ nói chung, từ bề mặt của Mặt Trời được xem là nguồn năng lượng chính cho Trái Đất. Hằng số năng lượng Mặt Trời được tính bằng công suất của lượng bức xạ trực tiếp chiếu trên một đơn vị diện tích bề mặt Trái Đất; nó bằng khoảng 1370 Watt trên một mét vuông.[138] Ánh sáng Mặt Trời bị hấp thụ một phần trên bầu khí quyển Trái Đất, nên một phần nhỏ hơn tới được bề mặt Trái Đất, gần 1.000 Watt/m² năng lượng Mặt Trời tới Trái Đất trong điều kiện trời quang đãng khi Mặt Trời ở gần thiên đỉnh.[139] Năng lượng này có thể dùng vào các quá trình tự nhiên hay nhân tạo. Quá trình quang hợp trong cây sử dụng ánh sáng mặt trời và chuyển đổi CO2 thành ôxy và hợp chất hữu cơ, trong khi nguồn nhiệt trực tiếp là làm nóng các bình đun nước dùng năng lượng Mặt Trời, hay chuyển thành điện năng bằng các pin năng lượng Mặt Trời. Năng lượng dự trữ trong dầu mỏ và các nguồn nhiên liệu hóa thạch khác được giả định rằng là nguồn năng lượng của Mặt Trời được chuyển đổi từ xa xưa trong quá trình quang hợp và phản ứng hóa sinh của sinh vật cổ.[140]
Mặt Trời và tác hại đến mắt[sửa | sửa mã nguồn]
Mặt Trời rất sáng, và nhìn trực tiếp vào Mặt Trời rất có hại cho mắt, nhưng không nghiêm trọng khi mắt mở bình thường hoặc không mở rộng.[141][142] Nhìn trực tiếp vào Mặt Trời vào lúc trưa nắng sẽ làm cho các sắc tố quang hình trong con ngươi mất màu tạm thời, có thể tạo ra hiện tượng đom đóm mắt và mù tạm thời. Nhìn thẳng vào Mặt Trời bằng mắt trần sẽ nhận khoảng 4 miliwatt ánh sáng vào con ngươi và làm nóng lên đủ để có thể gây tác hại do mắt không phản ứng kịp trước độ sáng. Nhìn thoáng qua Mặt Trời có thể gây cảm giác khó chịu nhưng không gây hại nhiều.[143][144]

Phân tích ánh sáng mặt trời khi đến Trái Đất
Nhìn Mặt Trời thông qua các thấu kính như ống nhòm rất có hại nếu không có màn chắn hấp thụ làm mờ tia sáng. Các màng làm mờ có bán tại các cửa hàng cung cấp sản phẩm hàn và máy chụp ảnh. Sử dụng đồ lọc thích hợp rất quan trọng như làm giảm độ sáng và cản các tia hồng ngoại và cực tím có thể làm hại cho mắt ở các cấp độ sáng cao.[145] Nhìn thẳng vào thấu kính để nhìn Mặt Trời có thể nhận khoảng 2 watt năng lượng trực tiếp vào mắt, gấp 500 lần hơn so với nhìn bằng mắt thường. Chỉ thoáng nhìn qua thấu kính mà không có đầu lọc có thể gây ra mù vĩnh viễn.[146]
Trong hiện tượng nhật thực, điều kiện nguy hiểm có thể xảy ra đối với mắt bởi phản ứng của mắt với ánh sáng. Đồng tử được điều khiển bằng tổng ánh sáng của môi trường, không bằng ánh sáng của vật sáng nhất trong môi trường. Trong hiện tượng nhật thực, phần lớn ánh sáng bị cản lại bằng Mặt Trăng, nhưng phần ánh sáng không bị che khuất có lượng ánh sáng bằng một ngày bình thường. Trong ánh sáng mờ, đồng tử có hiện tượng giãn nở từ 2 mm đến 6 mm, tăng điện tích tiếp nhận ánh sáng gấp 10 lần. Các phần tử trên con ngươi nhận trực tiếp từ ánh sáng Mặt Trời vì thế gấp 10 lần bình thường, hay lúc không nhật thực. Nhìn trực tiếp nhật thực bằng mắt thường có thể gây ra sự hủy hoại từng phần trên võng mạc, gây ra hiện tượng mù từng đốm trên mắt.[147] Điều này đặc biệt ảnh hưởng với trẻ em và những người không có kinh nghiệm.
Trong lúc Mặt Trời mọc hay lặn, ánh sáng bị hấp thụ một phần do khoảng đường xa tới tầng khí quyển Trái Đất,[148] ngoài ra ánh sáng còn bị làm mờ do bụi trong không khí, sương mù và độ ẩm trong không khí góp một phần trong sự hấp thu này nên không làm cho mắt khó chịu.[149]
Vòng đời của Mặt Trời[sửa | sửa mã nguồn]
Xem thêm: Sự hình thành và tiến hóa của Hệ Mặt Trời và Tiến hóa sao

Thời gian sẽ dừng lại khi Mặt Trời chết đi

Mặt Trời
Mặt Trời được hình thành cách đây khoảng 4,57 tỉ năm khi đám mây phân tử hydro tích tụ dần lại.[150] Tuổi của Mặt Trời được xác định theo 2 cách: tuổi của các sao ở dãy chính mà hiện tại Mặt Trời đang thuộc về nhóm này, được xác định thông qua các mô hình máy tính của sự kiện tiến hóa sao và niên đại học phóng xạ hạt nhân vào khoảng 4,57 tỉ năm.[151] Trong khi phương pháp định tuổi bằng đồng vị phóng xạ của các vật liệu cổ nhất từ hệ Mặt Trời vào khoảng 4,567 tỉ năm.[152][153]
Mặt Trời hiện đã tồn tại nửa vòng đời của nó theo tiến hóa của các sao dãy chính, trong khi các phản ứng tổng hợp hạt nhân trong lõi của nó chuyển hydro thành heli. Mỗi giây có hơn 4 triệu tấn vật chất trong lõi của Mặt Trời được chuyển thành năng lượng, tạo ra neutrino và các dạng bức xạ năng lượng Mặt Trời. Với tốc độ này cho đến nay, Mặt Trời đã chuyển đổi khoảng 100 lần khối lượng vật chất Trái Đất thành năng lượng. Mặt Trời sẽ mất tổng cộng khoảng 10 tỷ năm để kết thúc sự tồn tại của nó trước khi trở thành sao lùn trắng.[154]
Kết quả của sự tăng cường nguyên tử heli một cách từ từ trong lõi của Mặt Trời, độ sáng của ngôi sao này đang từ từ tăng lên. Độ sáng của Mặt Trời sẽ tăng 10% trong 1,1 tỷ năm tới, 40% sau 3,5 tỷ năm.[155]
Mặt Trời không có khối lượng đủ lớn để kết thúc vòng đời bằng một vụ nổ tung như siêu tân tinh. Ngược lại, trong vòng 4-5 tỷ năm tới nó sẽ đi tới trạng thái sao khổng lồ đỏ của mình, diễn ra khi nguồn hiđrô trong lõi cạn kiệt. Sau đó nó bắt đầu phun trào hêli và nhiệt độ phần lõi sẽ tăng lên đến 10 triệu K và sẽ tạo ra carbon để trở thành gần như là sao khổng lồ.[26] Các phản ứng nhiệt hạch sẽ sử dụng heli làm nguyên liệu tổng hợp nên các nguyên tố nặng hơn heli, làm cho lớp ngoài cùng của Mặt Trời sẽ giãn nở, đạt đến vị trí bên ngoài quỹ đạo Trái Đất hiện tại, 1 AU(1,5×1011 m), gấp 250 lần bán kính hiện tại của Mặt Trời.[156] Tuy nhiên, theo thời gian, khi đạt tới gần một sao khổng lồ đỏ, Mặt Trời sẽ mất đi khoảng 30% khối lượng hiện tại do gió Sao, vì thế các quỹ đạo của các hành tinh sẽ dần chuyển động ra xa. Nếu như thế sẽ làm quỹ đạo Trái Đất dịch ra xa hơn về phía bên ngoài, ngăn không cho nó bị nhấn chìm, nhưng các nghiên cứu mới cho thấy rằng Trái Đất sẽ bị Mặt Trời "nuốt chửng" do các tương tác thủy triều.[156]
Thậm chí nếu Trái Đất thoát khỏi ảnh hưởng của Mặt Trời, tất cả nước sẽ bị bốc hơi và hầu hết khí trong khí quyển sẽ thoát vào không gian. Trong trường hợp Mặt Trời còn nằm trong dãy chính, nó sẽ tỏa sáng hơn một cách dần dần (khoảng 10% mỗi một tỉ năm), và nhiệt độ bề mặt của nó sẽ tăng một cách chậm chạp. Mặt Trời từng là một ngôi sao mờ nhạt trong quá khứ của nó, đó cũng là lý do có thể hợp lý để giải thích sự sống trên Trái Đất chỉ tồn tại khoảng 1 tỉ năm trên đất liền. Nhiệt độ Mặt Trời gia tăng đã diễn ra trong khoảng 1 tỉ năm, bề mặt Trái Đất sẽ trở nên rất nóng để nước có thể tồn tại ở dạng lỏng và kết thúc tất cả sự sống Trái Đất.[156][157]
Sau giai đoạn đỏ khổng lồ, các xung nhiệt khổng lồ sẽ làm cho Mặt Trời phun ra các lớp bên ngoài của nó để tạo ra tinh vân. Mặt Trời sau đó sẽ trở thành sao lùn trắng, nguội dần đi vĩnh viễn. Kịch bản tiến hóa sao này là rất điển hình đối với những sao có khối lượng thấp đến trung bình.[158][159]
Thời gian biểu tiến hóa sao của Mặt Trời và hệ Mặt Trời[sửa | sửa mã nguồn]

Vòng đời của Mặt Trời (tỉ năm), từ trái sang:
Bắt đầu - Hiện tại - Nhiệt độ tăng dần - Sao khổng lồ đỏ - Suy sụp hấp dẫn - Sao lùn trắng...
Lấy mốc điểm khởi đầu hình thành hệ Mặt Trời khi sự nén ép trọng lực của tinh vân mặt trời tăng lên cách đây 5 tỉ năm.
- Tiền Mặt Trời: kéo dài từ hàng tỉ năm đến 50 triệu năm trước khi hình thành hệ Mặt Trời. Các đám mây tích tụ lại trong vùng bán kính 20 parsec.
- Hình thành Mặt Trời:
- 0 - 0,1x106 năm: Loạt bức xạ siêu tân tinh lân cận kích hoạt tạo ra các vùng đậm đặc vật chất trong đám mây phân tử
- 0,1x106 - 50x106 năm: Mặt Trời lúc này có dạng khởi thủy sao T-Tauri
- 0,1x106 - 10x106 năm: Hình thành các dạng đĩa tiền hành tinh của các hành tinh vòng ngoài, là sự tự tụ tập lại của vật chất phía diềm ngoài tinh vân Mặt Trời. Mặt Trời đặc lại và nóng lên, gió Mặt Trời thổi dạt các luồng khí liên hành tinh.
- 10x106 - 100x106 triệu năm: Hình thành các hành tinh kiểu đất đá vòng trong. Xuất hiện các va chạm lớn. Nước hình thành trên Trái Đất
- Tiến trình chính: Mặt Trời bắt đầu ổn định
- 200x106 năm: Đá cổ xưa nhất trên Trái Đất (đã quan sát thấy) hình thành.
- 500 - 600x106 năm: Cộng hưởng hấp dẫn do Sao Mộc và Sao Thổ đã kéo Sao Hải Vương về phía đĩa Kuiper. Một loạt các vụ va chạm giữa các thiên thể đã xảy ra thời kỳ này
- 800x106 năm: Mầm mống sự sống xuất hiện trên Trái Đất.
- 4,7 tỉ năm: Là giai đoạn ổn định hiện tại, với sự tăng cường độ sáng và nhiệt độ của Mặt Trời khoảng 10% mỗi tỉ năm.
- 6 tỉ năm: Biên bề mặt Mặt Trời có thể mở rộng vượt quá quỹ đạo Trái Đất tới quỹ đạo Sao Hỏa.
- 7 tỉ năm: Thiên hà Andromeda tiến dần về Ngân Hà và xuất hiện khả năng dù nhỏ có thể sẽ hút hệ Mặt Trời trước khi hai thiên hà hòa nhập.
- Hậu tiến trình chính, từ năm 10 tỉ - 12 tỉ: Giai đoạn sao khổng lồ đỏ theo tiến trình Hertzsprung-Russell.
- 10 - 12 tỉ năm: Mặt Trời bắt đầu bước vào quá trình đốt cháy hydro ở lớp ngoài lõi. Kể từ thời điểm này, nó đã không còn thuộc nhóm các ngôi sao thuộc dãy chínhnữa. Mặt Trời dần biến thành một sao khổng lồ đỏ theo hệ thống tiến trình Hertzsprung-Russell và tỏa sáng hơn gấp nhiều lần (độ sáng có thể gấp tới 2700 lần hiện tại), lớn hơn nhiều (bán kính tăng lên gấp 250 lần) và nguội đi (còn khoảng 2726,85 K). Với kích thước cực kì lớn, Mặt Trời sẽ nuốt trọn Sao Thủy và có thể cả Sao Kim và Trái Đất.
- Tới giai đoạn này, sau khi đã sử dụng hết hydro, Mặt Trời phải đốt tiếp heli để duy trì sự tồn tại. Nó dần dần trở thành một sao khổng lồ mặc dù đã mất đi 30% khối lượng so với thời kì cực thịnh. Tiếp theo đó, Mặt Trời đi đến giai đoạn bùng nổ, phun ra xung quanh một lượng lớn vật chất dưới dạng ion hóa và plasma. Lõi của nó sẽ trở thành một sao lùn trắng
- Tàn dư: Giai đoạn sao lùn trắng
- Ngoài 12 tỉ năm: Sao lùn trắng cạn kiệt dần năng lượng, nguội đi và trở thành sao lùn đen
- Ngoài 100 nghìn tỉ năm: Mặt Trời hạ nhiệt độ xuống chỉ còn vài độ K. Toàn bộ hệ Mặt Trời tham gia vào khối vật chất tối của vũ trụ





























