Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ví dụ về tập hợp: Toàn bộ học sinh lớp 10A
a) 3 ∈ Z
b) √2 ∉ Q

a) \(\left(P\Rightarrow Q\right):\)"Nếu \(x\) là một số hữu tỉ \(x^2\) cũng là một số hữu tỉ". Mệnh đề đúng.
b) Mệnh đề đảo là " Nếu \(x^2\) là một số hữu tỉ thì \(x\) là một số hữu tỉ"
c) Chẳng hạn, với \(x=\sqrt{2}\) mệnh đề này sai

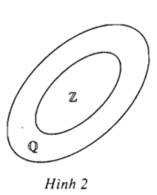
Tập hợp các số nguyên Z nằm trong tập hợp các số hữu tỉ Q
Có thể nói mỗi số nguyên là một số hữu tỉ

Nếu có P => Q thì ta gọi P là điều kiện cần của Q và đồng thời Q cũng là điều kiện đủ của P
Ta gọi mệnh đề P : a và b - chúng đều là 2 số hữu tỉ, Q : tổng a + b là số hữu tỉ
Mệnh đề ở gt : P => Q
Mệnh đề A : P => Q
Mệnh đề B : Q => P
Mệnh đề C : Q => P
Mệnh đề D : A,B,C đều sai
=> Do đó chúng ta chọn đáp án A là hợp lí nhất.

a) \(\exists a\in\mathbb{Z}:a=a^2\)
b) \(\forall x\in\mathbb{R}:x+0=x\)
c) \(\exists x\in\mathbb{Q}:x< \dfrac{1}{x}\)
d) \(\forall n\in\mathbb{N}:n>0\)

Mệnh đề P đúng, bình phương của một số thực luôn lớn hơn hoặc bằng 0 (không âm).
Mệnh đề Q sai vì \({x^2} = 2 \Leftrightarrow x = \pm \sqrt 2 \notin \mathbb Q\), do đó không có số hữu tỉ nào mà bình phương của nó bằng 2.
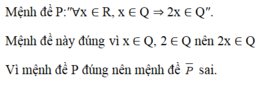
a) Mệnh đề “Mọi số nguyên đều viết được dưới dạng phân số” đúng.
Vì \(\forall a \in \mathbb{Z}:a = \dfrac{a}{1}\)
Hoặc: \(a \in \mathbb{Z} \subset \mathbb{Q}\) => mỗi số nguyên cũng là một phân số.
b) Mệnh đề "Tập hợp các số thực chứa tập hợp các số hữu tỉ" là mệnh đề đúng.
c) Mệnh đề “Tồn tại một số thực không là số hữu tỉ” đúng.
Ví dụ: \(\sqrt 2 \) ( vì \(\sqrt 2 \in \mathbb{R};\;\sqrt 2 \notin \mathbb{Q}\)).