Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lấy điểm O cố định rồi đặt \(\overrightarrow{OA_1}=\overrightarrow{a_1};\overrightarrow{OB_1}=\overrightarrow{b_1};\overrightarrow{OC_1}=\overrightarrow{c_1};\overrightarrow{OD_1}=\overrightarrow{d_1}\)
Điều kiện cần và đủ để tứ giác \(A_1B_1C_1D_1\) là hình bình hành là :
\(\overrightarrow{a_1}+\overrightarrow{c_1}=\overrightarrow{b_1}+\overrightarrow{d_1}\) (1)
\(\overrightarrow{a}+\overrightarrow{c}=\overrightarrow{b}+\overrightarrow{d}\Leftrightarrow\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{OB}+\overrightarrow{OD}\)
<=> Tứ giác ABCD là hình bình hành

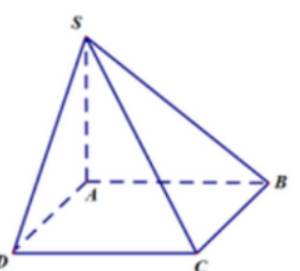
Hình chóp S.ABCD có các mặt bên là hình tam giác nên hình biểu diễn của nó cũng có các mặt bên là hình tam giác.
ABCD là hình bình hành nên hình biểu diễn của nó cũng là hình bình hành
Từ đó, ta vẽ được hình biểu diễn của hình chóp S.ABCD

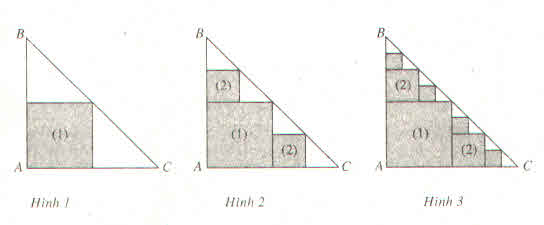
a) Hình vuông thứ nhất có cạnh bằng nên u1 = (
)2 =
.
Hình vuông thứ hai có cạnh bằng nên u2 = (
)2 =
.
Hình vuông thứ ba có cạnh bằng nên u3 = (
)2 =
.
Tương tự, ta có un =
b) Dãy số (un) là một cặp số nhân lùi vô hạn với u1 = và q =
. Do đó
lim Sn = .

Chọn B.
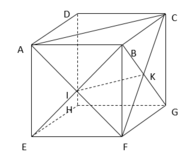
- Ta có:
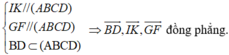
- + Các bộ véctơ ở phương án A, C, D không thể có giá cùng song song với một mặt phẳng.

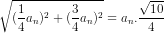 với n ε N*.
với n ε N*. 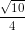

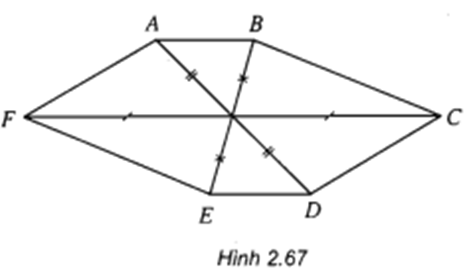


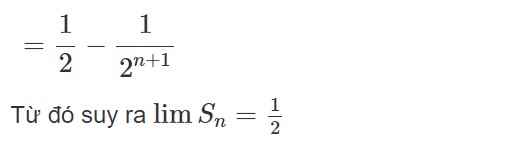
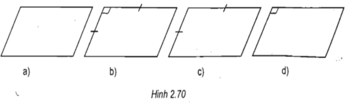
Hình 2.70a biểu diễn hình bình hành
Hình 2.70b biểu diễn hình vuông
Hình 2.70c biểu diễn hình thoi
Hình 2.70d biểu diễn hình chữ nhật