
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NV
1

Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
27 tháng 7 2017
Ta có 2005 – 1985 = 20 (năm). Vậy đầu năm 2005 ứng với t = 20. Số cần tìm

Chọn đáp án A.

CM
26 tháng 10 2018
Đáp án A
Phương pháp giải:
Để i n là số nguyên dương thì n là số nguyên dương chia hết cho 4
Lời giải:
Xét n=2k khi đó ![]() là số nguyên dương khi k chẵn.
là số nguyên dương khi k chẵn.
Kết hợp với ![]() suy ra
suy ra 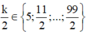 và
và ![]() là số chẵn.
là số chẵn.
Với mỗi bộ số 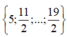 có 2 số k thỏa mãn,
có 2 số k thỏa mãn, 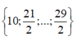 có 3 số k thỏa mãn.
có 3 số k thỏa mãn.
Vậy có tất cả 2.5+3.4=22 số thỏa mãn yêu cầu bài toán.
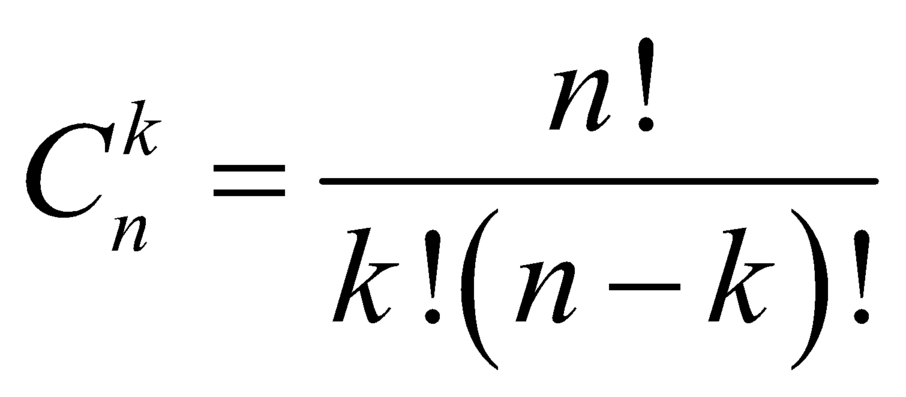 .
.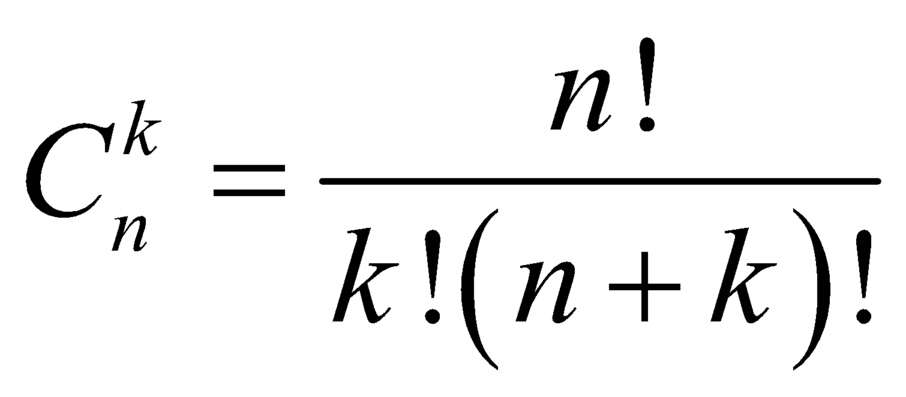 .
.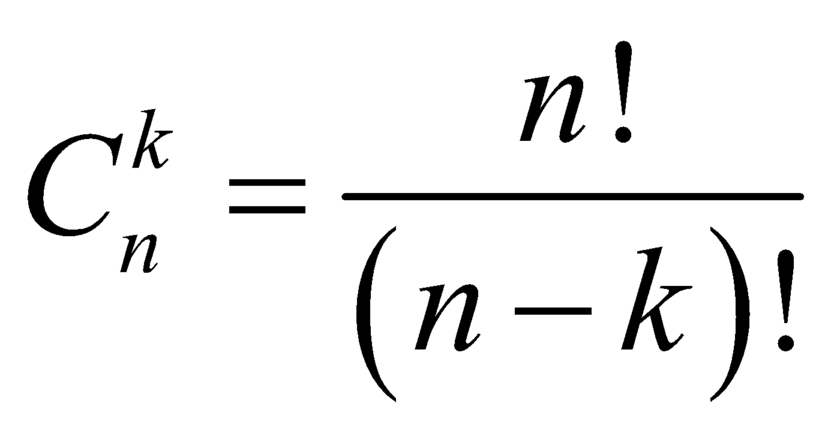 .
.
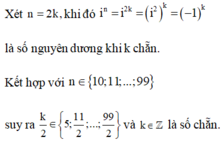

n!=1.2.3...nn!=1.2.3...n. Quy ước: 0!=10!=1
n!=(n−1)!nn!=(n−1)!n
n!p!=(p+1)(p+2)....nn!p!=(p+1)(p+2)....n (với n>pn>p)
n!(n−p)!=(n−p+1)(n−p+2)....nn!(n−p)!=(n−p+1)(n−p+2)....n (với n>pn>p)
2. Hoán vị (không lặp)
Một tập hợp gồm n phần tử (n≥1)(n≥1). Mỗi cách sắp xếp n phần tử này theo một thứ tự nào đó được gọi là một hoán vị của n phần tử.
Số hoán vị của n phần tử là Pn=n!Pn=n!
3. Hoán vị lặp
Cho k phần tử khác nhau a1;a2;...;aka1;a2;...;ak . Mỗi cách sắp xếp n phần tử trong đó gồm n1 phần tử a1; n2 phần tử a2;…; nk phần tử ak (n1+n2+...+nk=n)(n1+n2+...+nk=n) theo một thứ tự nào đó được gọi là một hoán vị lặp cấp n và kiểu (n1;n2;...;nk)(n1;n2;...;nk) của k phần tử
Số các hoán vị lặp cấp n kiểu (n1;n2;;;;nk)(n1;n2;;;;nk) của k phần tử là:
Pn(n1;n2;...;nk)=n!n1!n2!...nk!Pn(n1;n2;...;nk)=n!n1!n2!...nk!
HƯỚNG DẪN GIẢI