K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
6
HP
20 tháng 9 2021
3.
\(y=\dfrac{1-sin^24x}{5}=\dfrac{cos^24x}{5}\)
\(cos4x\in\left[-1;1\right]\Rightarrow cos^24x\in\left[0;1\right]\Rightarrow y\in\left[0;\dfrac{1}{5}\right]\Rightarrow\left\{{}\begin{matrix}y_{min}=0\\y_{max}=\dfrac{1}{5}\end{matrix}\right.\)
HP
20 tháng 9 2021
6.
\(y=sinx+cosx+2=\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)+2\)
\(sin\left(x+\dfrac{\pi}{4}\right)\in\left[-1;1\right]\Rightarrow y=\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)+2\in\left[-\sqrt{2}+2;\sqrt{2}+2\right]\)
\(\Rightarrow y_{min}=-\sqrt{2}+2\)
\(y_{max}=\sqrt{2}+2\)
30 tháng 5 2022
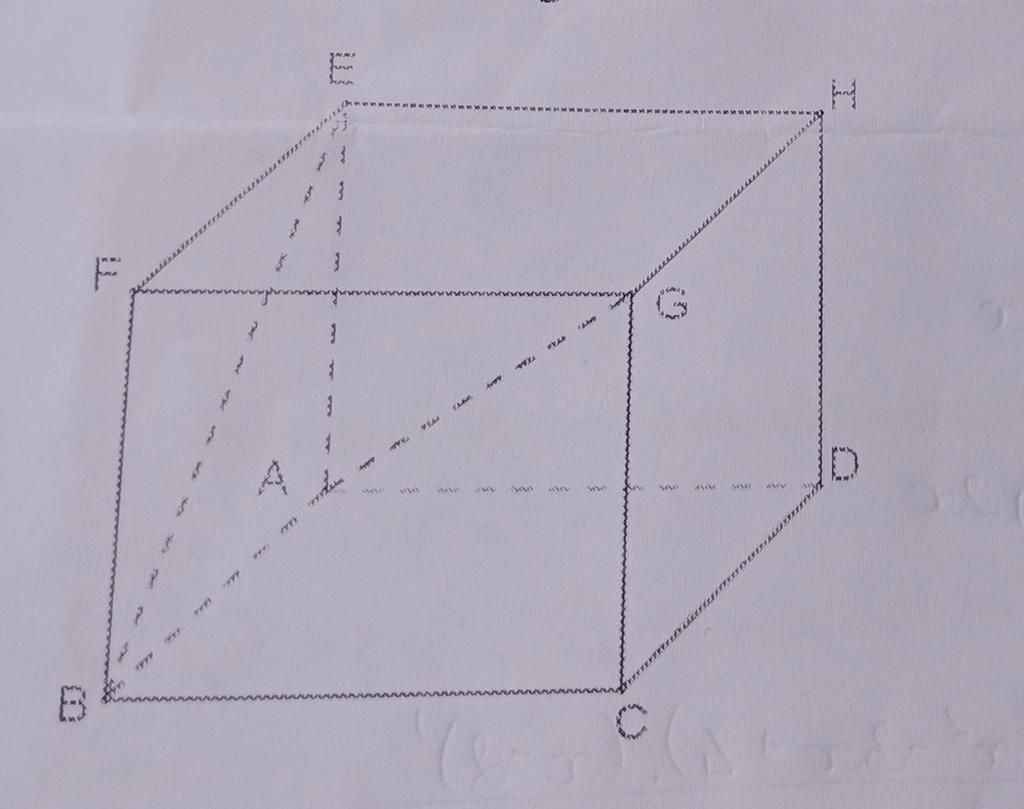
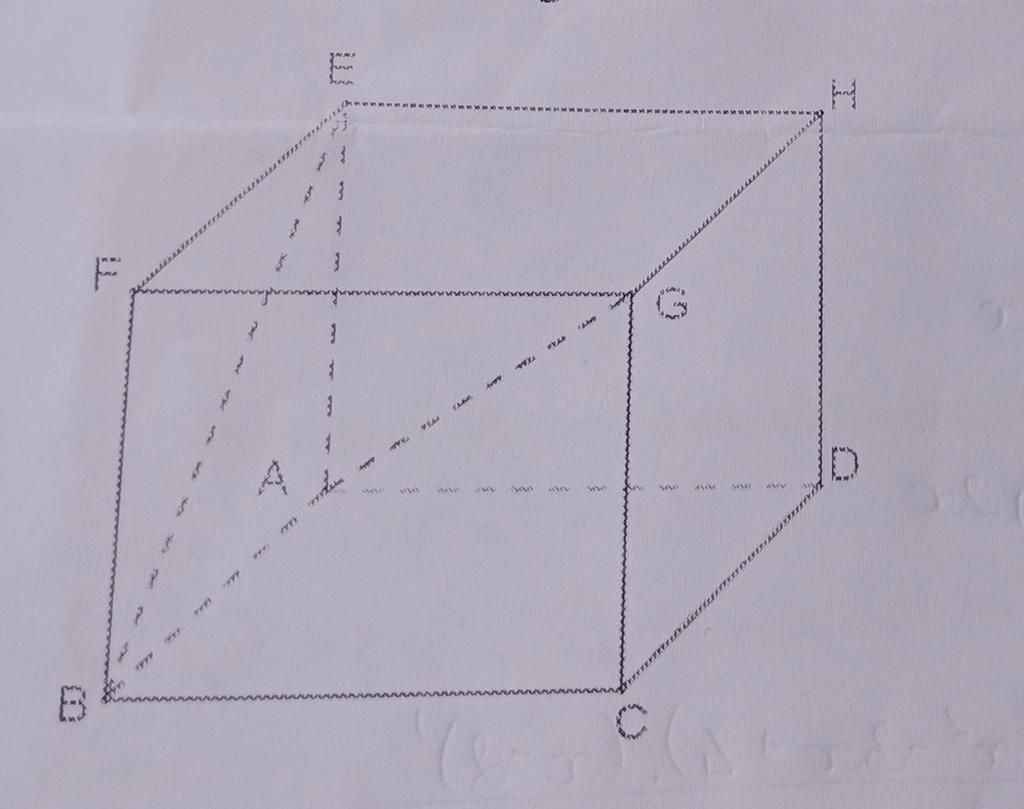
Đặt độ dài cạnh của hình lập phương là a
Ta có : \(\overrightarrow{AG}.\overrightarrow{BE}=\left(\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AE}\right)\left(\overrightarrow{AE}-\overrightarrow{AB}\right)\)
⇒ \(\overrightarrow{AG}.\overrightarrow{BE}=\overrightarrow{AB}.\overrightarrow{AE}-AB^2+\overrightarrow{AD}.\overrightarrow{AE}-\overrightarrow{AD}.\overrightarrow{AB}+AE^2-\overrightarrow{AE}.\overrightarrow{AB}\)
Các tích vô hướng ở vế phải bằng 0 và AE = AB
⇒ \(\overrightarrow{AG}.\overrightarrow{BE}=0\) ⇒ AG ⊥ BE, tức góc giữa hai đường thẳng này bằng 900
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 7 2021
- Mọi số nguyên n đều có số đối của nó là -n
- Do đó, trong biểu thức \(k2\pi\) nếu em thay k bằng số đối của nó là -k thì ta được \(-k2\pi\) thôi
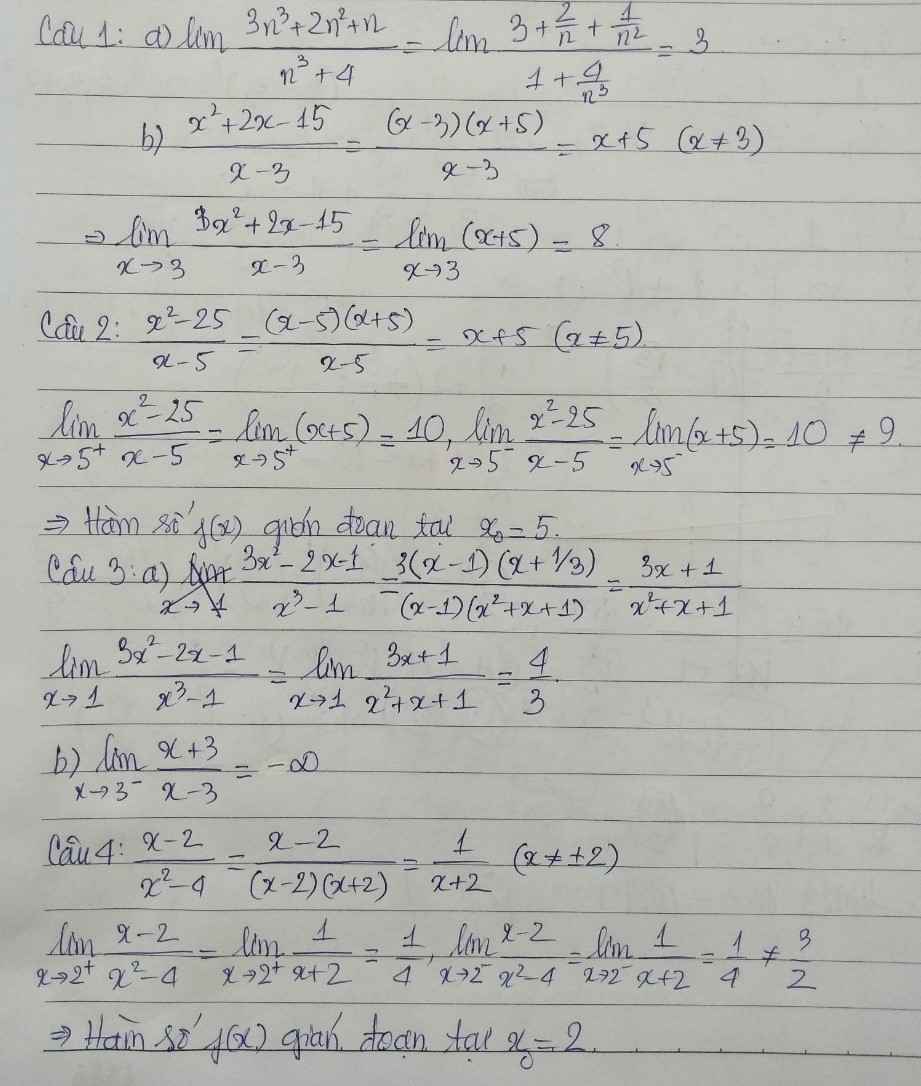
f/kkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkk