Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mỗi câu mình sẽ chia làm 2 phần( VT là ( 1 ) ,VP là ( 2 ) nha bạn !!!
a)
(1) (x -1)2 + 2 = (x-2)2
<=> x2 -2x + 1 + 2 =x2 - 4x + 4
<=> 2x = 1
<=> x = 1/2
(2) 2x3 -x2 + 2x - 1 = 0
<=> ( x - \(\frac{1}{2}\)) = 0
<=>x = 1/2
Vậy 2 PT trên tương đương
d)
(1) x + 1 = x là phương trình vô số no
(2) x3 + 1 = 0 là PT vô no
=> 2 pt trên không tương đương
c) và b) thì ...

a) \(x-\frac{1}{3}=0\Leftrightarrow x=\frac{1}{3}\)
Thay x=1/3 vào phương trình \(mx+2=0\):
\(\frac{m}{3}+2=0\Leftrightarrow m=-6\)
Vậy m=-6
b) \(2x-7=0\Leftrightarrow x=\frac{7}{2}\)
Thay x=7/2 vào phương trình (m-1)x-6=0:
\(\left(m-1\right)\cdot\frac{7}{2}-6=0\Leftrightarrow m-1=\frac{12}{7}\Leftrightarrow m=\frac{19}{7}\)
Vậy m=19/7
* Về cách trình bày, tớ ko chắc chắn là đúng.

b: Để hai phương trình này tương đương thì \(\left\{{}\begin{matrix}a\cdot\left(-1\right)+2=0\\2\cdot3+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=-6\end{matrix}\right.\)
a: Phương trình thứ hai thiếu vế phải rồi bạn

a) Đúng
b)Đúng
c)Sai vì nghiệm không thỏa mãn ĐKXĐ
d)Sai vì có 1 nghiệm không thỏa mãn ĐKXĐ

a)(2x+1)(3x-2)=(5x-8)(2x+1)
⇔(2x+1)(3x-2)-(5x-8)(2x+1)=0
⇔(2x+1)(3x-2-5x+8)=0
⇔(2x+1)(-2x+6)=0
⇔2x+1=0 hoặc -2x+6=0
1.2x+1=0⇔2x=-1⇔x=-1/2
2.-2x+6=0⇔-2x=-6⇔x=3
phương trình có 2 nghiệm x=-1/2 và x=3

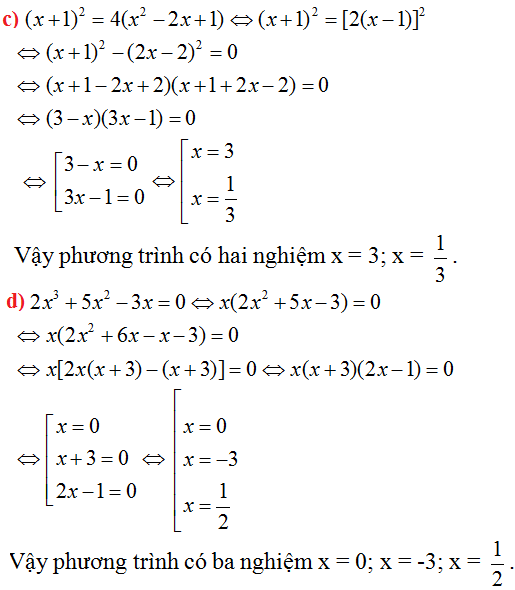
+)\(\left(x-1\right)^2+2=\left(x-2\right)^2\)
\(\Leftrightarrow\left(x-2\right)^2-\left(x-1\right)^2=2\)
\(\Leftrightarrow\left(x-2-x+1\right)\left(x-2+x-1\right)=2\)
\(\Leftrightarrow-1\left(2x-3\right)=2\)
\(\Leftrightarrow2x-3=-2\)
\(\Leftrightarrow2x=1\)
\(\Leftrightarrow x=\frac{1}{2}\)
Vậy tập nghiệm của pt 1 là \(S=\left\{\frac{1}{2}\right\}\)
+)\(2x^3-x^2+2x-1=0\)
\(\Leftrightarrow x^2\left(2x-1\right)+\left(2x-1\right)=0\)
\(\Leftrightarrow\left(2x-1\right)\left(x^2+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}2x-1=0\\x^2+1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\frac{1}{2}\\x^2=-1\left(\text{loại}\right)\end{cases}}}\)
Vậy tập nghiệm của pt 2 là \(S=\left\{\frac{1}{2}\right\}\)
Xét thấy 2 pt có tập nghiệm như nhau nên 2 pt này tương đương
*\(\left(x-1\right)^2+2=\left(x-2\right)^2\)
\(\Leftrightarrow x^2-2x+1+2=x^2-4x+4\)
\(\Leftrightarrow x^2-x^2-2x+4x=-1-2+4\)
\(\Leftrightarrow2x=1\Leftrightarrow x=\frac{1}{2}\)
Vậy phương trình có tập nghiệm S= { 1/2 } (1)
*\(2x^3-x^2+2x-1=0\)
\(\Leftrightarrow x^2\left(2x-1\right)+\left(2x-1\right)=0\)
\(\Leftrightarrow\left(2x-1\right)\left(x^2+1\right)=0\)
\(\Leftrightarrow2x-1=0\) ( vì x2 + 1 luôn khác 0 với mọi x )
\(\Leftrightarrow2x=1\Leftrightarrow x=\frac{1}{2}\)
Vậy phương trình có tập nghiệm là S = {1/2} (2)
Từ (1) và (2) suy ra : 2 phương trình đã cho tương đương nhau