
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\dfrac{x}{a}=\dfrac{m-\dfrac{x}{2}}{m}\)
\(\Rightarrow xm=a\left(m-\dfrac{x}{2}\right)\)
\(\Rightarrow xm=am-\dfrac{ax}{2}\)
\(\Rightarrow2xm=2am-ax\)
\(\Rightarrow2xm+ax=2am\)
\(\Rightarrow x\left(2m+a\right)=2am\)
\(\Rightarrow x=\dfrac{2am}{a+2m}\)

a, \(3x+7x^2+5+2x-7x^2\ge0\Leftrightarrow5x+5\ge0\Leftrightarrow x\ge-1\)
b, \(12x\ge-16\Leftrightarrow x\ge-\dfrac{4}{3}\)
c, \(\dfrac{5x-1-6}{6}-\dfrac{4\left(x+1\right)}{3}\le0\)
\(\Leftrightarrow\dfrac{5x-7-8\left(x+1\right)}{6}\le0\Rightarrow-3x-15\le0\Leftrightarrow x\le-5\)

a: Ta có: \(x^2-x+1\)
\(=x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)
d: Ta có: \(x^2-2x+\left|y+1\right|+5\)
\(=\left(x-1\right)^2+\left|y+1\right|+4\ge4\forall x,y\)
Dấu '=' xảy ra khi x=1 và y=-1

a. \(\widehat{DAB}=\widehat{ABC}=\widehat{BCE}=90^0\)
\(\widehat{ABD}=180^0-\widehat{ABC}-\widehat{EBC}=180^0-60^0-\left(180^0-\widehat{BCE}-\widehat{CEB}\right)=180^0-60^0-\left(180^0-60-\widehat{CEB}\right)=\widehat{CEB}\)\(\Rightarrow\)△ABD∼△CEB (g-g).
\(\Rightarrow\dfrac{AD}{CB}=\dfrac{AB}{CE}\Rightarrow AD.CE=CB.AB\Rightarrow AD.CE=a^2\) không đổi
b. \(\widehat{CAD}=\widehat{BAD}+\widehat{BAC}=60^0+60^0=\widehat{BCE}+\widehat{ACB}=\widehat{ACE}\)
\(\dfrac{AD}{CB}=\dfrac{AB}{CE}\Rightarrow\dfrac{AD}{AC}=\dfrac{AC}{CE}\)
\(\Rightarrow\)△ACD∼△CEA (c-g-c)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{ACD}=\widehat{CEA}\\\dfrac{CE}{AC}=\dfrac{EA}{CD}\end{matrix}\right.\)
\(\Rightarrow\)△ACK∼△AEC (g-g).
\(\Rightarrow\dfrac{CK}{EC}=\dfrac{AK}{AC}\Rightarrow\dfrac{CE}{AC}=\dfrac{CK}{AK}\)
\(\Rightarrow\dfrac{AE}{CD}=\dfrac{CK}{AK}\Rightarrow AE.AK=CD.CK\)

Bài 5 hình 1: (tự vẽ hình nhé bạn)
a) Xét ΔABD và ΔACB ta có:
\(\widehat{BAD}\)= \(\widehat{BAC}\) (góc chung)
\(\widehat{ABD}\)= \(\widehat{ACB}\) (gt)
=> ΔABD ~ ΔACB (g-g)
=> \(\dfrac{AB}{AC}\) = \(\dfrac{BD}{CB}\) = \(\dfrac{AD}{AB}\) (tsđd)
b) Ta có: \(\dfrac{AB}{AC}\) = \(\dfrac{AD}{AB}\) (cm a)
=> \(AB^2\) = AD.AC
=> \(2^2\) = AD.4
=> AD = 1 (cm)
Ta có: AC = AD + DC (D thuộc AC)
=> 4 = 1 + DC
=> DC = 3 (cm)
c) Xét ΔABH và ΔADE ta có:
\(\widehat{AHB}\) = \(\widehat{AED}\) (=\(90^0\))
\(\widehat{ADB}\) = \(\widehat{ABH}\) (ΔABD ~ ΔACB)
=> ΔABH ~ ΔADE
=> \(\dfrac{AB}{AD}\) = \(\dfrac{AH}{AE}\) = \(\dfrac{BH}{DE}\) (tsdd)
Ta có: \(\dfrac{S_{ABH}}{S_{ADE}}\) = \(\left(\dfrac{AB}{AD}\right)^2\)= \(\left(\dfrac{2}{1}\right)^2\)= 4
=> đpcm
Tiếp bài 5 hình 2 (tự vẽ hình)
a) Xét ΔABC vuông tại A ta có:
\(BC^2\) = \(AB^2\) + \(AC^2\)
\(BC^2\) = \(21^2\) + \(28^2\)
BC = 35 (cm)
b) Xét ΔABC và ΔHBA ta có:
\(\widehat{BAC}\) = \(\widehat{AHB}\) ( =\(90^0\))
\(\widehat{ABC}\) = \(\widehat{ABH}\) (góc chung)
=> ΔABC ~ ΔHBA (g-g)
=> \(\dfrac{AB}{BH}\) = \(\dfrac{BC}{AB}\) (tsdd)
=> \(AB^2\) = BH.BC
=> \(21^2\) = 35.BH
=> BH = 12,6 (cm)
c) Xét ΔABC ta có:
BD là đường p/g (gt)
=> \(\dfrac{AD}{DC}\) = \(\dfrac{AB}{BC}\) (t/c đường p/g)
Xét ΔABH ta có:
BE là đường p/g (gt)
=> \(\dfrac{HE}{AE}\) = \(\dfrac{BH}{AB}\) (t/c đường p/g)
Mà: \(\dfrac{AB}{BC}\) = \(\dfrac{BH}{AB}\) (cm b)
=> đpcm
d) Ta có: \(\left\{{}\begin{matrix}\widehat{HBE}+\widehat{BEH}=90^0\\\widehat{ABD}+\widehat{ADB=90^0}\\\widehat{HBE}=\widehat{ABD}\end{matrix}\right.\)
=> \(\widehat{BEH}=\widehat{ADB}\)
Mà \(\widehat{BEH}=\widehat{AED}\) (2 góc dd)
Nên \(\widehat{ADB}=\widehat{AED}\)
=> đpcm

mình tìm không tháy bạn ơi ~ chủ yếu là mình nhờ mấy bạn từng học qua rồi chỉ giúp những dạng chủ yếu,mẹo vặt các loại đấy bạn !! không phải mình tìm đề đâu ~~`


\(\left(x-1\right)\left(x+1\right)-x\left(x+3\right)=0\)
\(\Rightarrow x^2-1-x^2-3x=0\Rightarrow-1=3x\Rightarrow x=-\dfrac{1}{3}\)
\(\left(x-1\right)\left(x+2\right)-x\left(x+3\right)=0\)
\(\Rightarrow x^2-1-x^2-3x=0\)
\(\Rightarrow3x=-1\Rightarrow x=-\dfrac{1}{3}\)
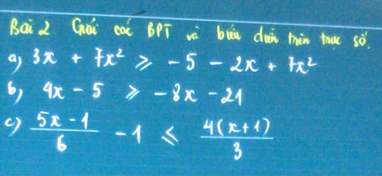
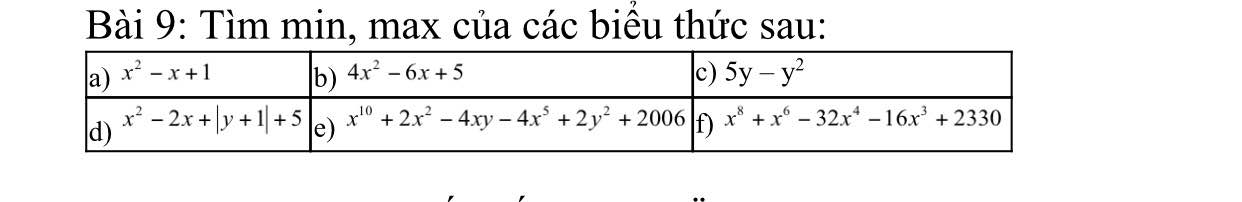

 giải hộ mình mấy bài này vs ạ !
giải hộ mình mấy bài này vs ạ !

