
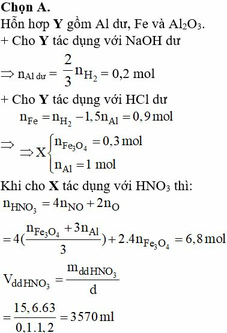
(1)...">
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời. Ta có : λo = 2300Ǻ = 2,3.10-7 (m). h= 6,625.10-34 (J.s), c = 3.108 m/s. Mặt khác: Theo định luật bảo toàn năng lượng và hiện tượng quang điện ta có công thức Thay số vào (1) ta có: Thầy xem hộ em lời giải của bài này ạ, em trình bày chưa được rõ ràng mong thầy sửa lỗi cho em ạ. em cám ơn thầy ạ! Năng lượng cần thiết để làm bật e ra khỏi kim loại Vonfram là: E===5,4eV Để electron bật ra khỏi kim loại thì ánh sáng chiếu vào phải có bước sóng ngắn hơn bước sóngtấm kim loại. Mà năng lượng ánh chiếu vào kim loại có E1<E nên electron không thể bật ra ngoài MgCO3 + 2HCl → MgCl2 + CO2 + H2O (1) BaCO3 + 2HCl → BaCl2 + CO2 + H2O (2) CO2 + Ca(OH)2 → CaCO3↓ + H2O. (3) Theo (1), (2) và (3), để lượng kết tủa B thu được là lớn nhất thì: nCO2 = nMgCO3 + nBaCO3 = 0,2 mol Ta có: => a = 29,89. Ta có: cos 450 = \(\frac{\text{ λ}}{\text{ λ}'}=\frac{\text{ λ}}{0,22}\) => λ = cos450.0,22 = 0.156Ǻ Thưa thầy, thầy chữa bài này được không ạ. Thầy ra lâu rồi nhưng chưa có đáp án đúng phương trình dạng toán tử : \(\widehat{H}\)\(\Psi\) = E\(\Psi\) Toán tử Laplace: \(\bigtriangledown\)2 = \(\frac{\partial^2}{\partial x^2}\)+ \(\frac{\partial^2}{\partial y^2}\)+\(\frac{\partial^2}{\partial z^2}\) thay vào từng bài cụ thể ta có : a.sin(x+y+z) \(\bigtriangledown\)2 f(x,y,z) = ( \(\frac{\partial^2}{\partial x^2}\)+ \(\frac{\partial^2}{\partial y^2}\)+\(\frac{\partial^2}{\partial z^2}\))sin(x+y+z) =\(\frac{\partial^2}{\partial x^2}\)sin(x+y+z) + \(\frac{\partial^2}{\partial y^2}\)sin(x+y+z) + \(\frac{\partial^2}{\partial z^2}\)sin(x+y+z) =\(\frac{\partial}{\partial x}\)cos(x+y+z) + \(\frac{\partial}{\partial y}\)cos(x+y+z) + \(\frac{\partial}{\partial z}\)cos(x+y+z) = -3.sin(x+y+z) \(\Rightarrow\) sin(x+y+z) là hàm riêng. với trị riêng bằng -3. b.cos(xy+yz+zx) \(\bigtriangledown\)2 f(x,y,z) = ( \(\frac{\partial^2}{\partial x^2}\)+ \(\frac{\partial^2}{\partial y^2}\)+\(\frac{\partial^2}{\partial z^2}\))cos(xy+yz+zx) =\(\frac{\partial^2}{\partial x^2}\)cos(xy+yz+zx) +\(\frac{\partial^2}{\partial y^2}\)cos(xy+yz+zx) + \(\frac{\partial^2}{\partial z^2}\)cos(xy+yz+zx) =\(\frac{\partial}{\partial x}\)(y+z).-sin(xy+yz+zx) + \(\frac{\partial}{\partial y}\)(x+z).-sin(xy+yz+zx) + \(\frac{\partial}{\partial z}\)(y+x).-sin(xy+yz+zx) =- ((y+z)2cos(xy+yz+zx) + (x+z)2cos(xy+yz+zx) + (y+x)2cos(xy+yz+zx)) =-((y+z)2+ (x+z)2 + (x+z)2).cos(xy+yz+zx) \(\Rightarrow\) cos(xy+yz+zx) không là hàm riêng của toán tử laplace. c.exp(x2+y2+z2) Thầy rất hoan nghênh bạn Thịnh đã trả lời câu hỏi 2, nhưng câu này em làm chưa đúng. Ở bài này các em cần phải vận dụng phương trình BET để tính diện tích bề mặt riêng: Sr = (Vm/22,4).NA.So. Sau khi thay số các em sẽ ra được đáp số. E làm thế này đúng không ạ? n(N2)=PV/RT=1*129*10^-3/(0.082*273)=5.76*10^-3 (mol) Độ hấp phụ: S=n(N2)/m=5.76*10^-3/1=5.76*10^-3 (mol/g) Diện tích bề mặt silicagel: S=N*So*J=6.023*10^23*16.2*10^-20*5.76*10^-3=562(m2/g) C2H2 + 2AgNO3 + 2NH3 → C2Ag2 ↓ + 2NH4NO3 CH3CHO + 2AgNO3 + 3NH3 + H2O → CH3COONH4 + 2Ag ↓ + 2NH4NO3 C2Ag2 + 2HCl → 2AgCl ↓ + C2H2 ↑ Y(AgCl, Ag) + HNO3 --> ... Ag + 2HNO3 → AgNO3 + NO2 ↑ + H2O Các cặp chất là đổng đẳng của nhau : C3H7OH và C4H9OH; CH3 - О - C2H5 và C2H3 - О - C2H5 Các cặp chất là đồng phân của nhau : CH3-O-C2H5 và C3H7OH; C2H5-O-C2H5 và C4H9OH. 
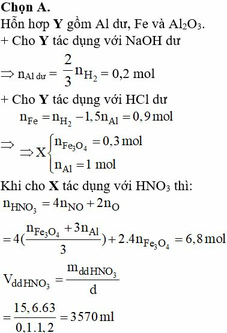

Emax=1,5( eV) = 1,5.1,6.10-19= 2,4.10-19(J)
(h.c)/ λ = (h.c)/ λo + Emax suy ra: λ=((h.c)/( (h.c)/ λo + Emax)) (1)
trong đó: λo : giới hạn quang điện của kim loại
λ: bước sóng của ánh sáng chiếu vào bề mặt kim loại để bứt electron ra khỏi bề mặt kimloại.
Emax: động năng ban đầu ( năng lượng của ánh sáng chiếu vào bề mặt kim loại).
λ = ((6,625.10-34.3.108)/((6,625.10-34.3.108)/(2,3.10-7) + (2,4.10-19)) = 1,8.10-7(m)
= 1800 Ǻ
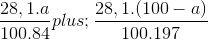 = 0,2
= 0,2



