MH
.jpg)
4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HT
4
HM
3
18 tháng 12 2016
I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các bài toán hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.
FA
15 tháng 9 2017
\(M=\left(x+2\right)\left(x+3\right)\left(x+4\right)\left(x+5\right)-24\)
\(M=\left[\left(x+2\right)\left(x+5\right)\right]\left[\left(x+3\right)\left(x+4\right)\right]-24\)
\(M=\left[x\left(x+5\right)+2\left(x+5\right)\right]\left[x\left(x+4\right)+3\left(x+4\right)\right]-24\)
\(M=\left(x^2+5x+2x+10\right)\left(x^2+4x+3x+12\right)-24\)
\(M=\left(x^2+7x+10\right)\left(x^2+7x+12\right)-24\)
\(M=\left(x^2+7x+11-1\right)\left(x^2+7x+11+1\right)-24\)
\(M=\left(x^2+7x+11\right)^2-1-24\)
\(M=\left(x^2+7x+11\right)^2-25\)
\(M=\left(x^2+7x+11+5\right)\left(x^2+7x+11-5\right)\)
\(M=\left(x^2+7x+16\right)\left(x^2+7x+6\right)\)
Giúp mình bài này với cô giáo mình giao trên mạng cô bảo cô bảo cho hướng dẫn nhưng lại k cho
15 tháng 5 2021
Câu 3:
Gọi số học sinh lớp 9A là \(x\)(học sinh) (điều kiện: \(x\inℕ^∗;x< 80\)).
Số học sinh lớp 9B là \(80-x\)(học sinh).
Tổng số quyển sách lớp 9A góp được trong đợt góp sách ủng hộ là \(2x\)(quyển sách).
Tổng số quyển sách lớp 9B góp được trong đợt góp sách ủng hộ là \(3\left(80-x\right)\)(quyển sách).
Vì lớp 9A và 9B góp được 198 quyển nên ta có phương trình:
\(2x+3\left(80-x\right)=198\).
\(\Leftrightarrow2x+240-3x=198\).
\(\Leftrightarrow2x-3x=198-240\).
\(\Leftrightarrow-x=-42\).
\(\Leftrightarrow x=42\)(thỏa mãn điều kiện).
Số học sinh lớp 9B là \(80-42=38\).
Vậy lớp 9A có 42 học sinh, lớp 9B có 38 học sinh.
21 tháng 7 2017
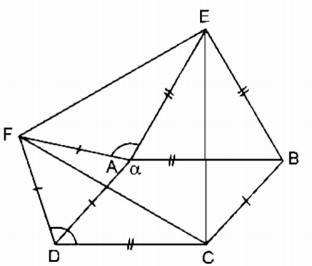
Kéo dài DF cắt AB tại E như sau:
 |
- Vì ABCD là hình thang nên AB , AE \(\backslash\backslash\) DC.
Suy ra, \(\widehat{EBF}=\widehat{DCF}\) (hai góc so le trong)
\(\widehat{BFE}=\widehat{CFD}\) (hai góc đối đỉnh).
Xét tam giác BEF và tam giác CDF có : \(\widehat{EBF}=\widehat{DCF}\) (cmt)
BF = FC ( F là trung điểm của BC)
\(\widehat{BFE}=\widehat{CFD}\) (cmt)
Vậy . tam giác BEF = tam giác CDF
Suy ra : FE = FD
Ta có : Diện tích hình ABDF + Diện tích hình CDF = Diện tích hình ABCD
Diện tích hình ABDF + Diện tích hình BEF = Diện tích hình ADE
Mà : tam giác BEF = tam giác CDF
Suy ra : diện tích ABCD bằng diện tích tam giác ADE
Với FE = FD, ta có hai tam giác ADF và AEF có đáy bằng nhau, cùng chung đường cao hạ từ A.
Suy ra, diện tích tam giác AFE bằng diện tích tam giác ADF.
Mà : diện tích tam giác AFE + diện tích tam giác ADF = diện tích tam giác ADE
Nên diện tích tam giác ADE bằng hai lần diện tích tam giác AFD và bằng : 2 x 10 = 20 cm2.
PT
3
28 tháng 8 2017
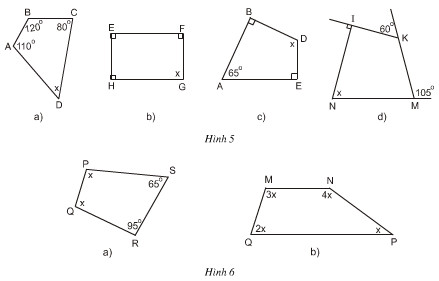
a) Ta có : A + B + C + D = 360o (4 góc trong 1 tứ giác)
Mà : A = 110o ; B = 120o ; C = 80o
Nên : 110o + 120o + 80o + D = 360o
Suy ra : D = 360o - 110o - 120o - 80o
Vậy D = 50o
VT
30 tháng 12 2017
bài 113 nâng cao và các chuyên đề toán 8 đại số (Vũ Dương Thụy -Nguyễn Ngọc Đạm)
DL
21 tháng 5 2019
https://i.vietnamdoc.net/data/image/2019/05/20/de-thi-hoc-ki-2-lop-8-mon-toan-truong-thcs-thai-thinh-dong-da-nam-hoc-2018-2019-1.jpg
link xem đề
Vì a=b=>a-b=0=>Từ (a-b)(a+b)=b(a-b) không thể suy ra a+b=b.
Điều này chỉ đúng khi b=0
dung ~~~~~~~a+b=b
a=b-b
a=0~~~~~~~~~~~~~a luon luon =0