K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
31 tháng 7 2021
Bài 2:
a) ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\notin\left\{4;9\right\}\end{matrix}\right.\)
b) Ta có: \(B=\dfrac{2\sqrt{x}-9}{x-5\sqrt{x}+6}-\dfrac{\sqrt{x}+3}{\sqrt{x}-2}-\dfrac{2\sqrt{x}+1}{3-\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}-9-\left(x-9\right)+\left(2\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{2\sqrt{x}-9-x+9+2x-4\sqrt{x}+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\cdot\left(\sqrt{x}-3\right)}\)
\(=\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)
c) Để B>1 thì B-1>0
\(\Leftrightarrow\dfrac{\sqrt{x}+1}{\sqrt{x}-3}-\dfrac{\sqrt{x}-3}{\sqrt{x}-3}>0\)
\(\Leftrightarrow\dfrac{4}{\sqrt{x}-3}>0\)
\(\Leftrightarrow\sqrt{x}>3\)
hay x>9
31 tháng 7 2021
Bài 2:
d) Để B nguyên thì \(\sqrt{x}+1⋮\sqrt{x}-3\)
\(\Leftrightarrow4⋮\sqrt{x}-3\)
\(\Leftrightarrow\sqrt{x}-3\in\left\{-2;-1;1;2;4\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{1;2;4;5;7\right\}\)
hay \(x\in\left\{1;16;25;49\right\}\)
29 tháng 6 2021
a, Ta có : \(A=\dfrac{1}{x+\sqrt{x}}+\dfrac{1}{\sqrt{x}+1}=\dfrac{1}{\sqrt{x}\left(\sqrt{x}+1\right)}+\dfrac{1}{\sqrt{x}+1}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}\left(1+\sqrt{x}\right)}=\dfrac{1}{\sqrt{x}}\)
\(\Rightarrow P=\dfrac{A}{B}=\dfrac{\dfrac{1}{\sqrt{x}}}{\dfrac{2}{\sqrt{x}+1}}=\dfrac{1}{\sqrt{x}}.\dfrac{\sqrt{x}+1}{2}=\dfrac{\sqrt{x}+1}{2\sqrt{x}}\)
b, Ta có : \(P=\dfrac{\sqrt{x}+1}{2\sqrt{x}}=\dfrac{1}{2}+\dfrac{1}{2\sqrt{x}}\)
Mà \(x>0\)
\(\Rightarrow\dfrac{1}{2\sqrt{x}}>0\)
\(\Rightarrow P>\dfrac{1}{2}\)
Vậy ...
29 tháng 6 2021
\(\begin{cases}\dfrac{1}{x+3}-\dfrac{2}{y-1}=9\\\dfrac{3}{x+3}+\dfrac{1}{y-1}=6\\\end{cases}\)
`<=>` \(\begin{cases}\dfrac{1}{x+3}-\dfrac{2}{y-1}=9\\\dfrac{6}{x+3}+\dfrac{2}{y-1}=12\\\end{cases}\)
`<=>` \(\begin{cases}\dfrac{7}{x+3}=21\\\dfrac{3}{x+3}+\dfrac{1}{y-1}=6\\\end{cases}\)
`<=>` \(\begin{cases}\dfrac{1}{x+3}=3\\\dfrac{3}{x+3}+\dfrac{1}{y-1}=6\\\end{cases}\)
`<=>` \(\begin{cases}x+3=\dfrac13\\\dfrac{1}{y-1}=6-9=-3\\\end{cases}\)
`<=>` \(\begin{cases}x=\dfrac{-8}{3}\\y=\dfrac23\\\end{cases}\)
29 tháng 6 2021
ĐKXĐ : \(\left\{{}\begin{matrix}x\ne-3\\y\ne1\end{matrix}\right.\)
- Đặt \(\left\{{}\begin{matrix}\dfrac{1}{x+3}=a\\\dfrac{1}{y-1}=b\end{matrix}\right.\)
HPTTT : \(\left\{{}\begin{matrix}a-2b=9\\3a+b=6\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a-2b=9\\6a+2b=12\end{matrix}\right.\)
- Cộng hai phương trình ta được : 7a = 21
=> a = 3
=> b = -3
- Thay lại hệ phương trình ta được ; \(\left\{{}\begin{matrix}\dfrac{1}{x+3}=3\\\dfrac{1}{y-1}=-3\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{8}{3}\\y=\dfrac{2}{3}\end{matrix}\right.\) ( TM )
Vậy ..
29 tháng 6 2021
`a)B=(1/(sqrtx-3)+4/(x-9))(sqrtx-3)`
`=((sqrtx+3)/(x-9)+4/(x-9))(sqrtx-3)`
`=(sqrtx+7)/(x-9)*(sqrtx-3)`
`=(sqrtx+7)/(sqrtx+3)`
`b)P=A:B`
`sqrtx/(sqrtx+3):(sqrtx+7)/(sqrtx+3)`
`=sqrtx/(sqrtx+7)`
Vì `x>=0=>sqrtx>=0`
`x>=0=>sqrtx+7>=7>0`
`=>P>=0`
Dấu "=" xảy ra khi `x=0`
`
29 tháng 6 2021
a, ĐKXĐ : \(\left\{{}\begin{matrix}x\ge0\\x\ne9\end{matrix}\right.\)
Ta có : \(B=\left(\dfrac{1}{\sqrt{x}-3}+\dfrac{4}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\right).\sqrt{x-3}\)
\(=1+\dfrac{4}{\sqrt{x}+3}=\dfrac{\sqrt{x}+3+4}{\sqrt{x}+3}=\dfrac{\sqrt{x}+7}{\sqrt{x}+3}\)
b, Ta có : \(P=\dfrac{\dfrac{\sqrt{x}}{\sqrt{x}+3}}{\dfrac{\sqrt{x}+7}{\sqrt{x}+3}}=\dfrac{\sqrt{x}}{\sqrt{x}+7}\)
- Thấy : \(\left\{{}\begin{matrix}\sqrt{x}\ge0\\\sqrt{x}+7>0\end{matrix}\right.\)
\(\Rightarrow P\ge0\)
Vậy \(MinP=0\Leftrightarrow x=0\)
29 tháng 6 2021
ĐKXĐ : \(\left\{{}\begin{matrix}x\ne2\\y\ne1\end{matrix}\right.\)
- Đặt \(\left\{{}\begin{matrix}\dfrac{1}{x-2}=a\\\dfrac{1}{y-1}=b\end{matrix}\right.\)
\(HPTTT\left\{{}\begin{matrix}2a+b=2\\4a-3b=1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}4a+2b=4\\4a-3b=1\end{matrix}\right.\)
- Trừ hai vế => b = 3/5
=> a = 7/10 .
- Thay lại ta được ; \(\left\{{}\begin{matrix}\dfrac{1}{x-2}=\dfrac{7}{10}\\\dfrac{1}{y-1}=\dfrac{3}{5}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{24}{7}\\y=\dfrac{8}{3}\end{matrix}\right.\) ( TM )
Vậy ..
16 tháng 8 2021
\(1,\) Khi \(x=9\) thì \(A=\dfrac{x+\sqrt{x}+4}{\sqrt{x}-2}=\dfrac{9+\sqrt{9}+4}{\sqrt{9}-2}=16\)
\(2,\) Ta có \(B=\dfrac{3x-4}{x-2\sqrt{x}}-\dfrac{\sqrt{x}+2}{\sqrt{x}}+\dfrac{\sqrt{x}-1}{2-\sqrt{x}}\left(x>0;x\ne4\right)\)
\(B=\dfrac{3x-4-\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)-\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}\left(\sqrt{x}-2\right)}\\ B=\dfrac{3x-4-x+4-x+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-2\right)}=\dfrac{x+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-2\right)}\\ B=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-2}\)
16 tháng 8 2021
1: Thay x=9 vào A,ta được:
\(A=\dfrac{9+3+4}{3-2}=16\)
2: Ta có: \(B=\dfrac{3x-4}{x-2\sqrt{x}}-\dfrac{\sqrt{x}+2}{\sqrt{x}}+\dfrac{\sqrt{x}-1}{2-\sqrt{x}}\)
\(=\dfrac{3x-4-\left(x-4\right)-\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
\(=\dfrac{3x-4-x+4-x+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-2}\)
1 tháng 4 2021
a) Ta có: \(\text{Δ}=\left(-2\right)^2-4\cdot1\cdot\left(m-3\right)=4-4m+12=-4m+16\)
Để phương trình có hai nghiệm thì \(\text{Δ}\ge0\)
\(\Leftrightarrow-4m+16\ge0\)
\(\Leftrightarrow-4m\ge-16\)
hay \(m\le4\)
1 tháng 4 2021
Ta có: \(\Delta'=4-m\)
a) Để phương trình có 2 nghiệm \(\Leftrightarrow\Delta'\ge0\) \(\Leftrightarrow m\le4\)
b) Theo Vi-ét, ta có: \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=m-3\end{matrix}\right.\)
Ta có: \(x_1^3+x_2^3=-20\)
\(\Rightarrow\left(x_1+x_2\right)\left(x_1^2+x_2^2-x_1x_2\right)=-20\)
\(\Rightarrow\left(x_1+x_2\right)\left[\left(x_1+x_2\right)^2-3x_1x_2\right]=-20\)
\(\Rightarrow2\left[2^2-3\left(m-3\right)\right]=-20\)
\(\Leftrightarrow8-6m+18=-20\) \(\Leftrightarrow m=\dfrac{23}{3}\) (Thỏa mãn)
Vậy \(m=\dfrac{23}{3}\)
5 tháng 10 2021
\(A=\sqrt{2}\left(\dfrac{2+\sqrt{3}}{2+\sqrt{4+2\sqrt{3}}}+\dfrac{2-\sqrt{3}}{2-\sqrt{4-2\sqrt{3}}}\right)\\ A=\sqrt{2}\left(\dfrac{2+\sqrt{3}}{2+\sqrt{3}+1}+\dfrac{2-\sqrt{3}}{2-\sqrt{3}+1}\right)\\ A=\sqrt{2}\left(\dfrac{2+\sqrt{3}}{3+\sqrt{3}}+\dfrac{2-\sqrt{3}}{3-\sqrt{3}}\right)\\ A=\sqrt{2}\cdot\dfrac{\left(2+\sqrt{3}\right)\left(3-\sqrt{3}\right)+\left(2-\sqrt{3}\right)\left(3+\sqrt{3}\right)}{6}\\ A=\sqrt{2}\cdot\dfrac{3+\sqrt{3}+3-\sqrt{3}}{6}=\dfrac{6\sqrt{2}}{6}=\sqrt{2}\)
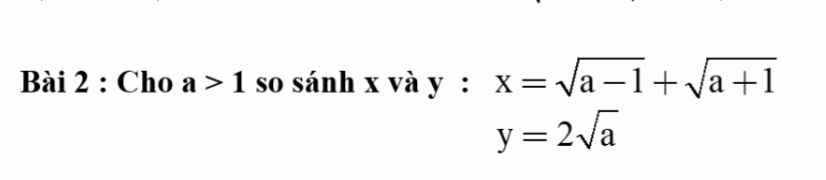
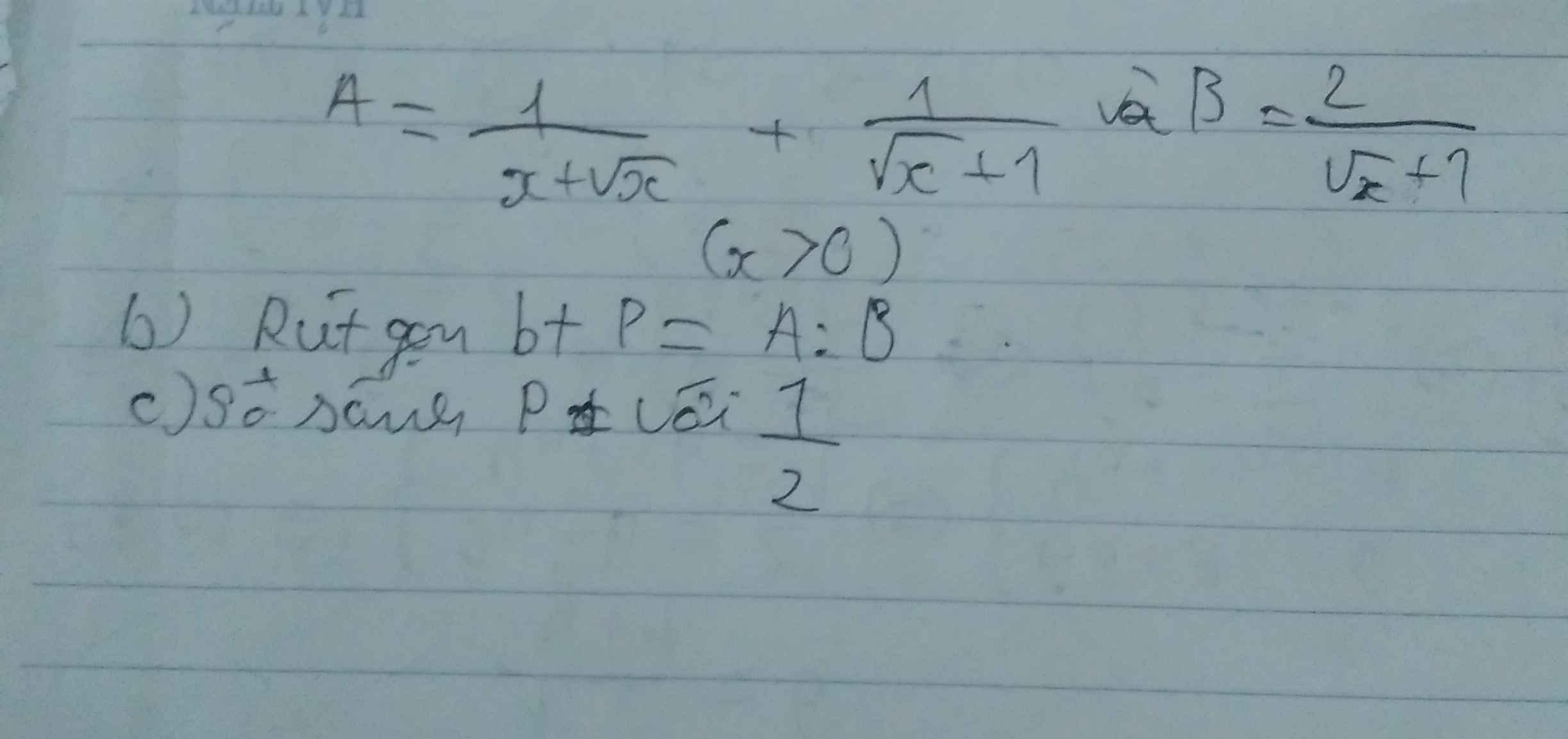
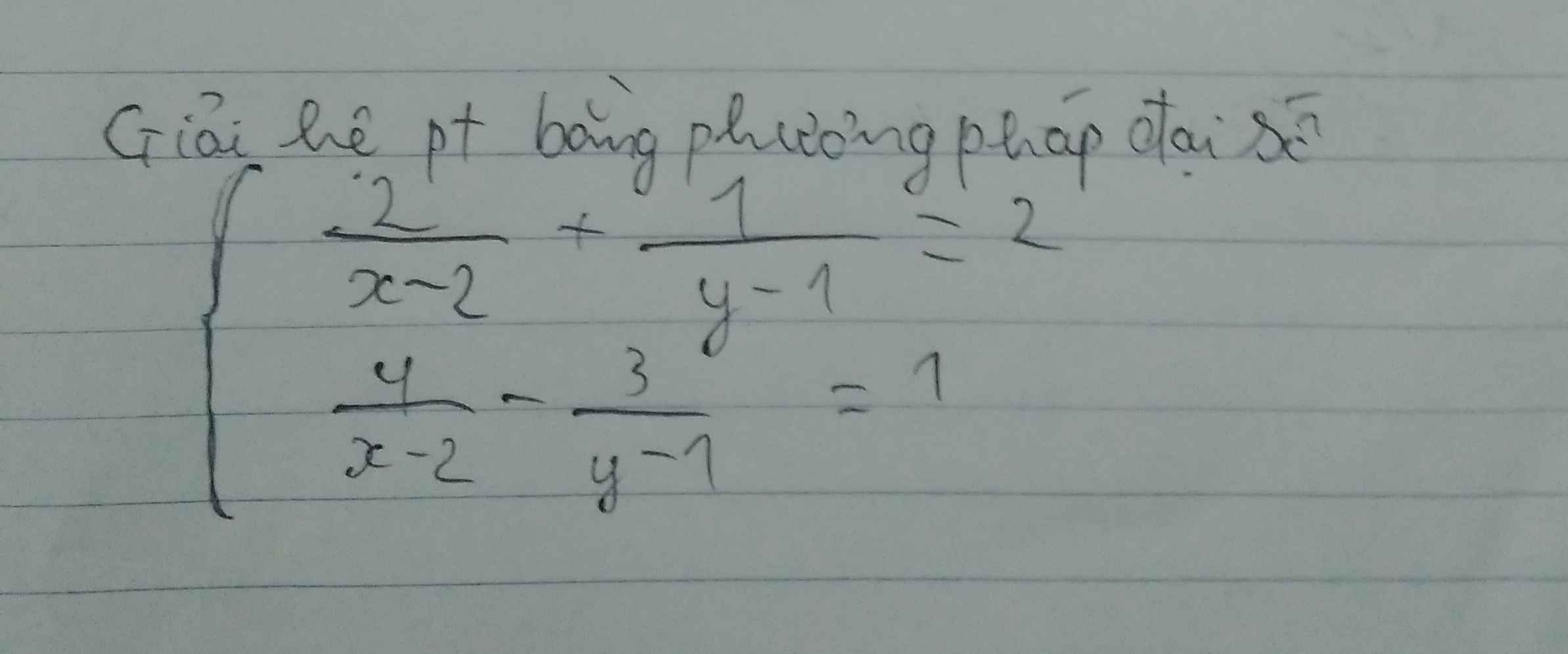
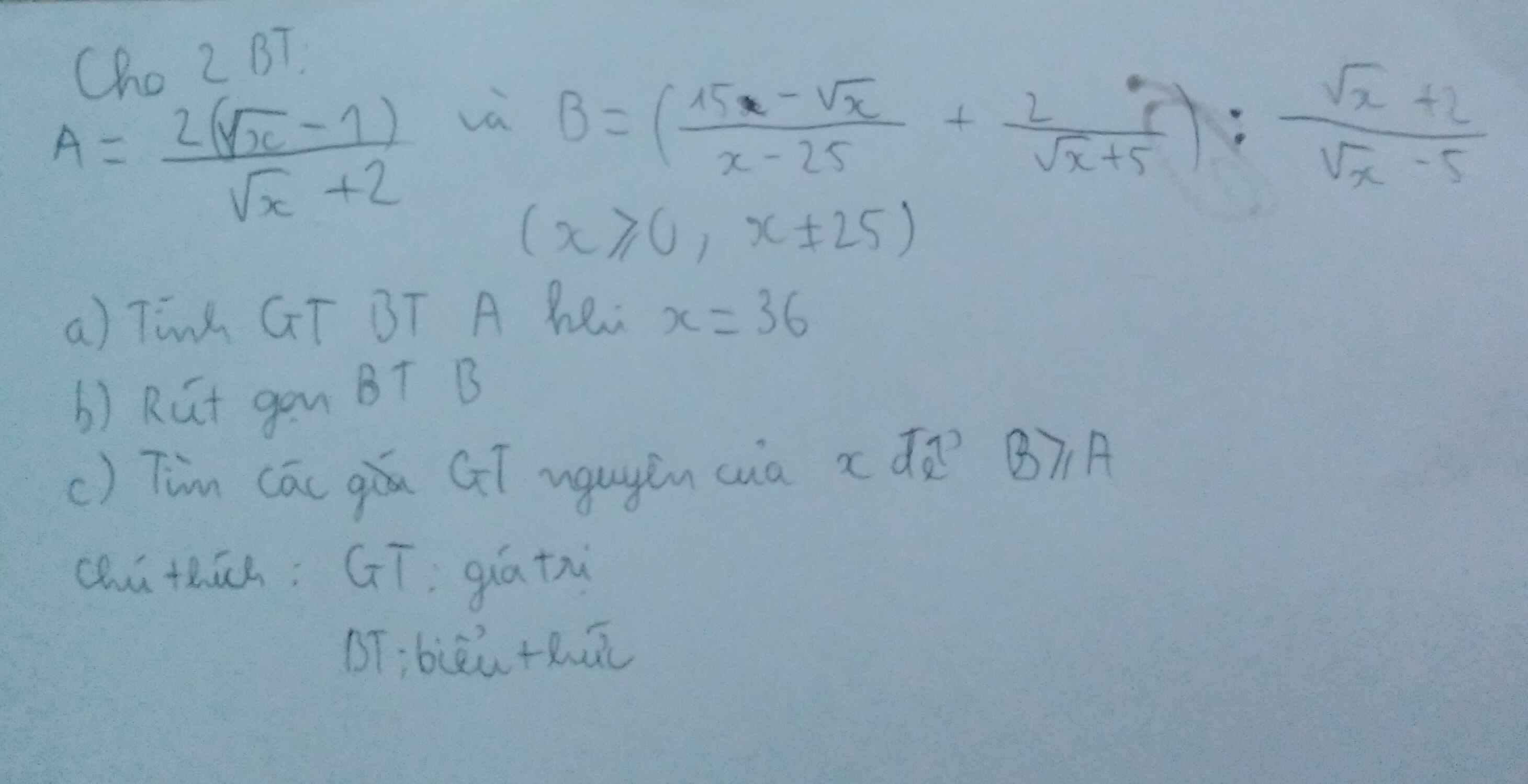
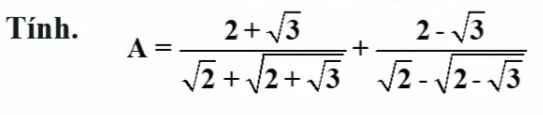
\(x^2=a-1+a+1+2\sqrt{\left(a-1\right)\left(a+1\right)}=2a+2\sqrt{\left(a-1\right)\left(a+1\right)}\)
Áp dụng BĐT cosi cho 2 số \(a-1;a+1>0\)
\(2a+2\sqrt{\left(a-1\right)\left(a+1\right)}\le2a+\left(a-1\right)+\left(a+1\right)=2a+2a=4a\)
Mà \(y^2=4a\)
Vậy \(x^2< y^2\Leftrightarrow x< y\)