K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
các bạn giúp mình với mình đang cần gấp
D
15 tháng 12 2022
B3
1) \(\sqrt{ }\)(2x-1)2 =5
\(\Leftrightarrow\) |2x-1| =5
\(\Leftrightarrow\) 2x-1 =5 hoặc 2x -1 = -5
\(\Leftrightarrow\) 2x=6 hoặc 2x= -4
\(\Leftrightarrow\) x=3 hoặc x= -2
2) 4-5x = 144
\(\Leftrightarrow\) -5x =140
\(\Leftrightarrow\) x= -60
3) \(\sqrt{ }\)(2x-2)2=2x-2
\(\Leftrightarrow\) | 2x -2 | =2x-2
\(\Leftrightarrow\) 2x-2 =2x-2 hoặc 2x-2 =-2x +2
\(\Leftrightarrow\) 0x=0 (loại ) hoặc x=2 ( nhận )
MH
1
AH
Akai Haruma
Giáo viên
15 tháng 12 2022
Bạn nên tách lẻ các bài ra post riêng. Đăng thế này chiếm diện tích, khó quan sát => mọi người dễ bỏ qua bài của bạn.
M
2
25 tháng 6 2021
19) Ta có: \(\sqrt[3]{x^3+9x^2}=x+3\)
\(\Leftrightarrow x^3+9x^2=\left(x+3\right)^3\)
\(\Leftrightarrow x^3+9x^2=x^3+9x^2+27x+27\)
\(\Leftrightarrow27x+27=0\)
\(\Leftrightarrow27x=-27\)
hay x=-1
Vậy: S={-1}
6) Ta có: \(\sqrt{9x^2-6x+1}-x=4\)
\(\Leftrightarrow\sqrt{\left(3x-1\right)^2}=x+4\)
\(\Leftrightarrow\left|3x-1\right|=x+4\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-1=x+4\left(x\ge\dfrac{1}{3}\right)\\1-3x=x+4\left(x< \dfrac{1}{3}\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-x=4+1\\-3x-x=4-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=5\\-4x=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\left(nhận\right)\\x=\dfrac{-3}{4}\left(nhận\right)\end{matrix}\right.\)
Vậy: \(S=\left\{\dfrac{5}{2};\dfrac{-3}{4}\right\}\)
25 tháng 6 2021
8)
ĐKXĐ: \(x>2\)
Ta có: \(\sqrt{x^2+2x+4}=x-2\)
\(\Leftrightarrow x^2+2x+4=\left(x-2\right)^2\)
\(\Leftrightarrow x^2+2x+4-x^2+4x-4=0\)
\(\Leftrightarrow6x=0\)
hay x=0(loại)
Vậy: \(S=\varnothing\)
9) Ta có: \(\sqrt{x^2-6x+9}=5\)
\(\Leftrightarrow\sqrt{\left(x-3\right)^2}=5\)
\(\Leftrightarrow\left|x-3\right|=5\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=5\\x-3=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-2\end{matrix}\right.\)
Vậy: S={8;-2}
NP
2
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 1 2022
22.
ĐKXĐ: \(y\ne1\)
\(\left\{{}\begin{matrix}x^2-\dfrac{1}{y-1}=2\\2x^2+\dfrac{3}{1-y}=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x^2+\dfrac{2}{1-y}=4\\2x^2+\dfrac{3}{1-y}=2\end{matrix}\right.\)
Trừ pt dưới cho trên:
\(\Rightarrow\dfrac{1}{1-y}=-2\)
\(\Rightarrow1-y=-\dfrac{1}{2}\Rightarrow y=\dfrac{3}{2}\)
Thế vào \(x^2-\dfrac{1}{y-1}=2\)
\(\Rightarrow x^2=4\Rightarrow x=\pm2\)
Vậy nghiệm của hệ là \(\left(x;y\right)=\left(2;\dfrac{3}{2}\right);\left(-2;\dfrac{3}{2}\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 1 2022
b.
ĐKXĐ: \(x\ne-\dfrac{1}{2}\)
\(Hệ\Leftrightarrow\left\{{}\begin{matrix}2y^2-\dfrac{10}{2x+1}=8\\2y^2-\dfrac{11}{2x+1}=7\end{matrix}\right.\)
Trừ pt trên cho dưới:
\(\Rightarrow\dfrac{1}{2x+1}=1\)
\(\Rightarrow2x+1=1\)
\(\Rightarrow x=0\)
Thế vào \(y^2-\dfrac{5}{2x+1}=4\)
\(\Rightarrow y^2=9\Rightarrow y=\pm3\)
Vậy nghiệm của hệ là \(\left(x;y\right)=\left(0;3\right);\left(0;-3\right)\)
AH
Akai Haruma
Giáo viên
23 tháng 5 2021
Lời giải:
Cộng 3 PT lại ta có:
$x(a+b+c)+y(a+b+c)=a+b+c$
$\Leftrightarrow (a+b+c)(x+y-1)=0$
$\Rightarrow a+b+c=0$ hoặc $x+y-1=0$
TH1: $a+b+c=0\Leftrightarrow a+b=-c$
Khi đó: $a^3+b^3+c^3=(a+b)^3-3ab(a+b)+c^3$
$=(-c)^3-3ab(-c)+c^3=3abc$
$\Rightarrow \frac{a^2}{bc}+\frac{b^2}{ac}+\frac{c^2}{ab}=3$ (đpcm)
TH2: $x+y-1=0\Leftrightarrow y=1-x$
Thay vô hpt \(\left\{\begin{matrix} ax+b(1-x)=c\\ bx+c(1-x)=a\\ cx+a(1-x)=b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x(a-b)=c-b\\ x(b-c)=a-c\\ x(c-a)=b-a\end{matrix}\right.\)
\(\Rightarrow x^3(a-b)(b-c)(c-a)=(c-b)(a-c)(b-a)=-(a-b)(b-c)(c-a)\)
\(\Leftrightarrow (a-b)(b-c)(c-a)(x^3+1)=0\)
Nếu $a-b=0$ thì kéo theo $b-c=c-a=0$
$\Rightarrow a=b=c$
Nếu $b-c=0; c-a=0$ thì tương tự
Nếu $x^3+1=0\Leftrightarrow x=-1$
$\Rightarrow b-a=c-b=a-c\Rightarrow a=b=c$
Tóm lại $a=b=c$
Do đó: $\frac{a^2}{bc}+\frac{b^2}{ac}+\frac{c^2}{ab}=1+1+1=3$ (đpcm)
E
1
8 tháng 8 2021
ta có sinB=\(\dfrac{AH}{AB}\)\(\Rightarrow\)AH=AB.sinB=3,6.sin62=3,18
BH=\(\sqrt{AB^2-AH^2}\)(pytago)=\(\sqrt{3,6^2-3,18^2}\)=1,69
\(_{\widehat{C}}\)=90-\(\widehat{B}\)=90-62=28\(^0\)
sinC=\(\dfrac{AB}{BC}\)\(\Rightarrow\)BC=\(\dfrac{AB}{sinC}\)=\(\dfrac{3,6}{sin28}\)=7,67
mà:CH=BC-BH=7,67-1,69=5,98
AC=\(\sqrt{BC^2-AB^2}\)(pytago)=\(\sqrt{7,67^2-3,6^2}\)=6.77
???
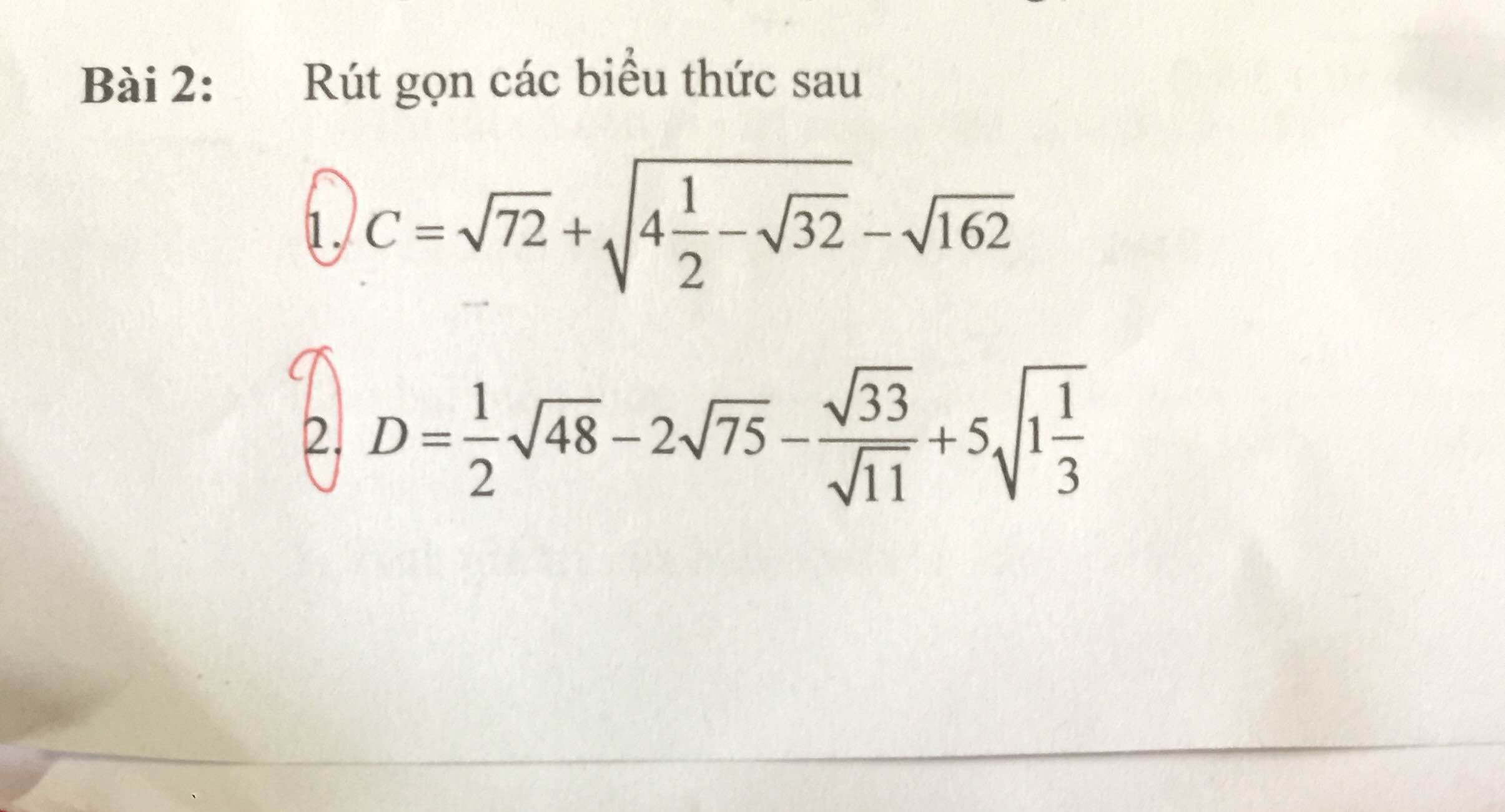
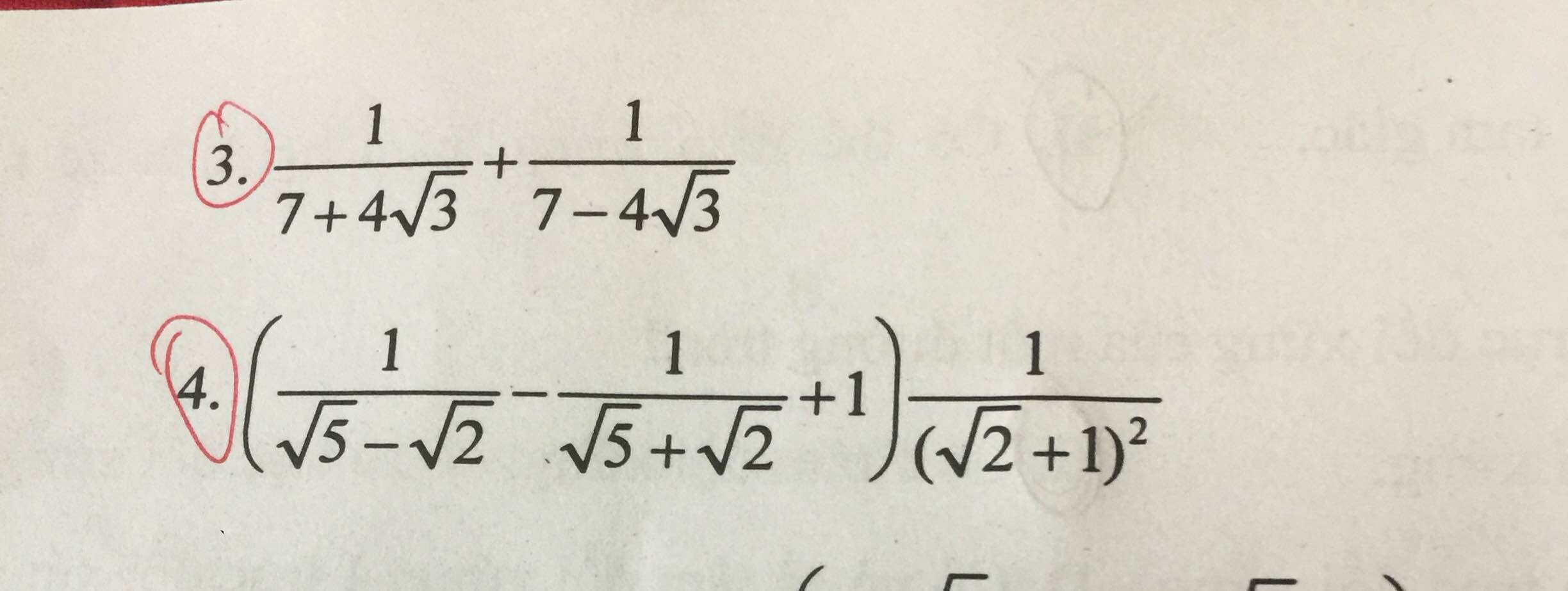
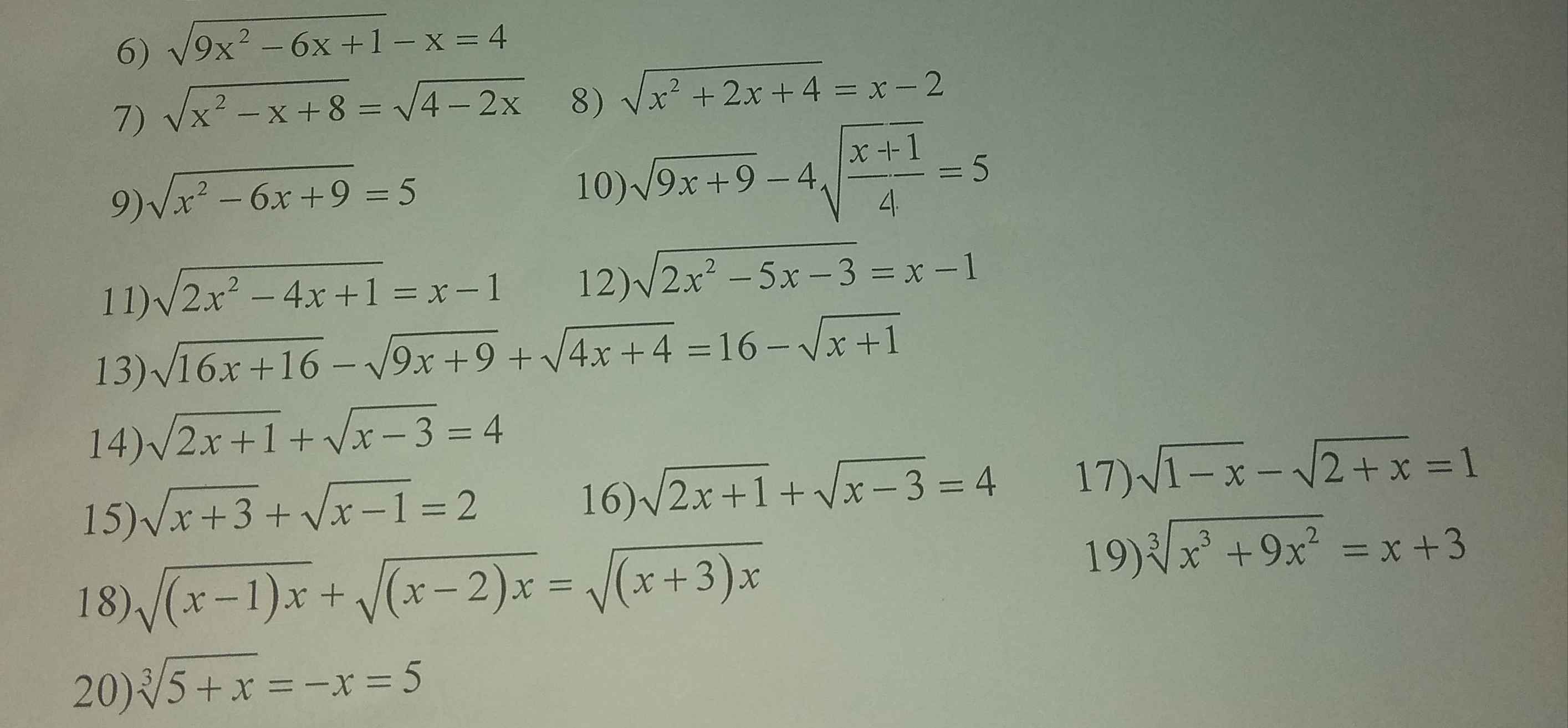
Lỗi