
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


4.6
Ta có: \(\widehat{ABC}+\widehat{DCB}=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên AB//CD

gọi (d) y=x
Thay x=1=>y=1=> (1;1)
Thay x=2=>y=2=> (2;2)
gọi (d1) y=-2x
Thay x=-1=> y=2=> (-1;2)
Thay x=1=>y=-2=> (1;-2)


1000+ 2000= 3000
Mik đầu tiên
Mik chọn quà 1, bạn k cho mik nha

đáng lẽ kiểm số nhưng t2 khai giảng, t4 hc hình nên cô cho đề dễ lắm, cho hai đt bị 1 đt cắt tạo thành các góc. nêu tên các góc = nhau
đề tùy trg nhé
r`, đây là 2 bài tiêu biểu khó nhất trong = í bài theo như bn t ns c` vs t 2 bài này bt
1) Tìm x;y thuộc N sao cho:
3x.4y = 12x
2) Cho m = 334
a) Tìm tất cả các ước của m. Tính tổng các ước đó
b) Tìm số dư trong phép chia 335 cho 13 (không dùng đồng dư thức)

=>1/2.2/3.3/4 = ab.bc.ca
<=> 1/4 = (abc)^2
=> abc = 1/2 hoặc abc = -12
=> a=4/3 ; b = 2/3 ; c=1 hoặc a=-4/3 ; b=-2/3 ; c=-1
k mk nha
Ta có: ab.bc.ac = \(\frac{1}{2}\). \(\frac{2}{3}\).\(\frac{3}{4}\)= \(\frac{1}{4}\)
\(\Leftrightarrow\)(abc)2 =\(\frac{1}{4}\)
\(\Leftrightarrow\)abc = \(\pm\) \(\sqrt{\frac{1}{4}}\)= \(\pm\)\(\frac{1}{2}\)
\(\Rightarrow\)\(\hept{\begin{cases}a=\pm\frac{3}{4}\\b=\pm\frac{2}{3}\\c=\pm1\end{cases}}\)

A) Xét tam giác ABH và tam giác ADH có :
HB=HD ( giả thiết)
HA ( cạnh chung)
góc DHA=góc BHA=90độ
suy ra tam giác ABH=tam giác ADH ( C-G-C)
B)Xét tam giác EHD và tam giác BHAcó:
HE=HA( GT)
góc AHB=góc DHE(hai góc đối đỉnh )
HD=HB( GT)
vậy suy ra : tam giácBHA= tam giác EHD( C-G-C)
vậy BA=ED( hai cạnh tương ứng)
C)ta gọi giao điểm của ED và AC là I
ta có góc IEA = góc EAB( hai góc tương ứng)
mà hai góc này lại ở
vị trí sole trong ở hai đoạn thẳng BA và EI
suy ra : BAsong song với EI
mà ta lại có góc BAI = 90 độ mà lại bù nhau với góc EIA vậy góc EIA =180 độ - 90 độ =90 độ
vậy EI vuong góc với AC

a, Tam giác ABC cân tại A
\(\Rightarrow\widehat{B}=\widehat{C}=\frac{180^o-\widehat{A}}{2}=\frac{180^o-40^o}{2}=70^o\)
b, Tam giác ABC cân tại B
\(\Rightarrow\widehat{A}=\widehat{C}=\frac{180^o-\widehat{B}}{2}=\frac{180^o-100^o}{2}=40^o\)
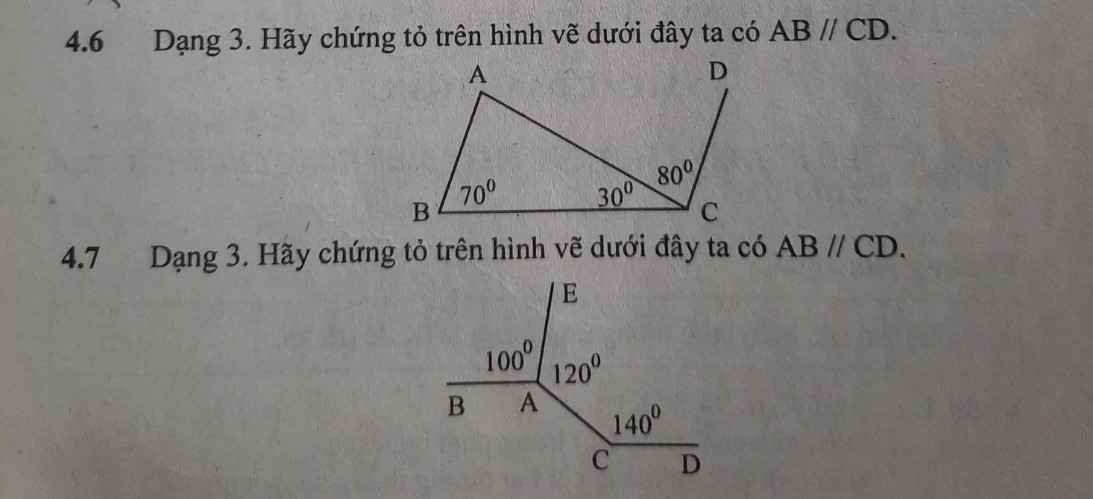
 cho tam giác ABC cân
cho tam giác ABC cân