Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số đo cạnh 1,cạnh 2,cạnh 3 lần lượt là:a,b,c(cm)(đk:a,b,c>0)
Vì cạnh 1,2,3 lần lượt tỉ lệ vs 2,3,4 nên:\(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}\)(1)
Vì chu vi tam giác là 45cm nên:a+b+c=45(2)
Từ (1) và (2). Áp dụng tính chất dãy tỉ số = nhau:
\(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}=\frac{a+b+c}{2+3+4}=\frac{45}{9}=5\)
Vậy \(\frac{a}{2}=5\)suy ra: a=2.5=10
\(\frac{b}{3}=5\)suy ra:a=3.5=15
\(\frac{c}{4}=5\)suy ra:c=4.5=20
Vậy cạh 1 là 10cm
cạnh 2 là 15cm
cạnh 3 là 20cm

ta có: x=0,8y và y=5z(đề bài )
nên x=0,8y=0,8.5z=4z
Vậy x tỉ lệ thuận vs z theo hệ số 4
Theo điều kiện đề bài ta có:
x=0,8y và y=5z nên:
x=0,8y=0,8.5z=4z
Vậy x tỉ lệ thuận với z theo hệ số tỉ lệ là 4


\(\frac{2}{4}=\frac{3}{6}=\frac{2+3}{4+6}\)
\(\frac{2}{4}=\frac{3}{6}=\frac{2-3}{4-6}\)
\(\Rightarrow\frac{2+3}{4+6}=\frac{2-3}{4-6}\)


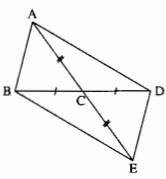
Giải
Ta có: ∆ACB = ∆ ECD(c.g.c)
∆ACD = ∆ECB(c.g.c)
∆ABD = ∆EDB(c.g.c)
∆ABE = ∆EDA(c.g.c)
A B C D E
Ta có: ∆ACB = ∆ ECD(c.g.c)
∆ACD = ∆ECB(c.g.c)
∆ABD = ∆EDB(c.g.c)
∆ABE = ∆EDA(c.g.c)
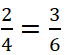
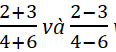 với các tỉ số trong tỉ lệ thức đã cho.
với các tỉ số trong tỉ lệ thức đã cho.
a)
b)Ta có: \(\frac{s}{t}=\frac{12}{1}=\frac{24}{2}=\frac{36}{3}=\frac{48}{4}=\frac{60}{5}=12\)
\(\Rightarrow\)s=12.t\(\Rightarrow\)s tỉ lệ thuận với t theo hệ số tỉ lệ 12