
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


4: \(D=x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)
\(A=\left(x^2-6x+9\right)-7=\left(x-3\right)^2-7\ge7\\ A_{min}=7\Leftrightarrow x=3\\ B=\left(9x^2+6x+1\right)-4=\left(3x+1\right)^2-4\ge-4\\ B_{min}=-4\Leftrightarrow x=-\dfrac{1}{3}\\ C=\left(x^2-2\cdot\dfrac{5}{2}x+\dfrac{25}{4}\right)-\dfrac{9}{4}=\left(x-\dfrac{5}{2}\right)^2-\dfrac{9}{4}\ge-\dfrac{9}{4}\\ C_{min}=-\dfrac{9}{4}\Leftrightarrow x=\dfrac{5}{2}\\ D=\left(x^2-x+\dfrac{1}{4}\right)+\dfrac{3}{4}=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\\ D_{min}=\dfrac{3}{4}\Leftrightarrow x=\dfrac{1}{2}\)
\(E=3\left(x^2+2\cdot\dfrac{1}{3}x+\dfrac{1}{9}\right)-\dfrac{4}{3}=3\left(x+\dfrac{1}{3}\right)^2-\dfrac{4}{3}\ge-\dfrac{4}{3}\\ E_{min}=-\dfrac{4}{3}\Leftrightarrow x=-\dfrac{1}{3}\\ F=x^2-2x+1+x^2-4x+4+2021\\ F=2\left(x^2-3x+\dfrac{9}{4}\right)+\dfrac{4031}{2}=2\left(x-\dfrac{3}{2}\right)^2+\dfrac{4031}{2}\ge\dfrac{4031}{2}\\ F_{min}=\dfrac{4031}{2}\Leftrightarrow x=\dfrac{3}{2}\)

a)999x1001=(1000-1)(1000+1)=10002-12=1000000-1=999999
b)bạn viết đúng đề câu b k thế?

cô làm rồi em ơi https://olm.vn/cau-hoi/bai-3-tu-giac-abcd-co-goc-c-goc-d-90-do-chung-minh-rang-ac2-bd-ab2cd2.8140260328277

Bài 11:
a: \(4x^2-1=\left(2x-1\right)\left(2x+1\right)\)
b: \(25x^2-\dfrac{9}{100}=\left(5x-\dfrac{3}{10}\right)\left(5x+\dfrac{3}{10}\right)\)
c: \(9x^2-\dfrac{1}{4}=\left(3x-\dfrac{1}{2}\right)\left(3x+\dfrac{1}{2}\right)\)
d: \(\left(x-y\right)^2-4=\left(x-y-2\right)\left(x-y+2\right)\)

a, 4\(x^3\).y + \(\dfrac{1}{2}\)yz
=y.(4\(x^3\) + \(\dfrac{1}{2}\)z)
b, (a2 + b2 - 5)2 - 2.(ab + 2)2
= [a2 + b2 - 5 - \(\sqrt{2}\)(ab + 2) ].[ a2 + b2 - 5 + \(\sqrt{2}\)(ab +2)]
a) \(4x^3y+\dfrac{1}{2}yz=y\left(4x^3+\dfrac{1}{2}z\right)\)
b) \(\left(a^2+b^2-5\right)^2-2.\left(ab+2\right)^2\)
\(=\left[\left(a^2+b^2-5\right)+2\left(ab+2\right)\right]\left[\left(a^2+b^2-5\right)-2\left(ab+2\right)\right]\)
\(=\left[a^2+b^2-5+2ab+4\right]\left[a^2+b^2-5-2ab-4\right]\)
\(=\left[a^2+b^2+2ab-1\right]\left[a^2+b^2-2ab-9\right]\)
\(=\left[\left(a+b\right)^2-1\right]\left[\left(a-b\right)^2-9\right]\)
\(=\left[\left(a+b+1\right)\left(a+b-1\right)\right]\left[\left(a-b+3\right)\left(a-b-3\right)\right]\)

Lời giải:
Vì $x=9$ nên $x-9=0$
Ta có:
$F=(x^{2017}-9x^{2016})-(x^{2016}-9x^{2015})+(x^{2015}-9x^{2014})-....-(x^2-9x)+x-10$
$=x^{2016}(x-9)-x^{2015}(x-9)+x^{2014}(x-9)-....-x(x-9)+x-10$
$=x^{2016}.0-x^{2015}.0+x^{2014}.0-...-x.0+x-10$
$=x-10=9-10=-1$

\(=\frac{\left(x^3\right)^2-\left(y^3\right)^2}{\left[\left(x^2\right)^2-\left(y^2\right)^2\right]-xy\left(x^2-y^2\right)}=\)
\(=\frac{\left(x^3-y^3\right)\left(x^3+y^3\right)}{\left(x^2-y^2\right)\left(x^2+y^2\right)-xy\left(x^2-y^2\right)}=\)
\(=\frac{\left(x+y\right)\left(x^2-xy+y^2\right)\left(x-y\right)\left(x^2+xy+y^2\right)}{\left(x^2-y^2\right)\left(x^2+y^2-xy\right)}=\)
\(=\frac{\left(x^2-y^2\right)\left(x^2-xy+y^2\right)\left(x^2+xy+y^2\right)}{\left(x^2-y^2\right)\left(x^2-xy+y^2\right)}=x^2+xy+y^2\)

a: Xét tứ giác AEMF có
\(\widehat{MEA}=\widehat{MFA}=\widehat{FME}=90^0\)
Do đó: AEMF là hình chữ nhật
a)Tứ giác AEMF có :
\(\widehat{MEA}=\widehat{MFA}=\widehat{FME}=90^0\)
=>AEMF là hình chữ nhật

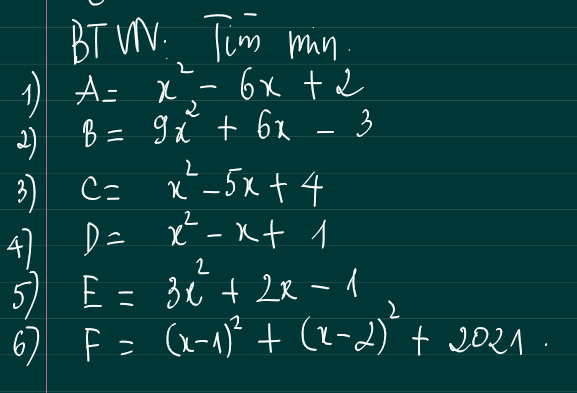

 CÁC BẠN GIÚP MÌNH NHÉ MÌNH CẢM ƠN
CÁC BẠN GIÚP MÌNH NHÉ MÌNH CẢM ƠN
Bài 3:
a) \(A=\left(2xy^2\right)\left(x^3-2xy+2y^2\right)\)
\(A=2xy^2\cdot x^3-2xy^2\cdot2xy+2xy^2\cdot2y^2\)
\(A=2x^4y^2-4x^2y^3+4xy^4\)
b) \(B=\left(x^2+y^2-z^2\right)\left(x^2+y^2+z^2\right)\)
\(B=x^2\cdot x^2+x^2\cdot y^2+x^2\cdot z^2+x^2\cdot y^2+y^2\cdot y^2+y^2\cdot z^2-x^2\cdot z^2-y^2\cdot z^2-z^2\cdot z^2\)
\(B=x^4+x^2y^2+x^2z^2+x^2y^2+y^4+y^2z^2-x^2z^2-y^2z^2-z^4\)
\(B=x^4+\left(x^2y^2+x^2y^2\right)+\left(x^2z^2-x^2z^2\right)+y^4+\left(y^2z^2-y^2z^2\right)-z^4\)
\(B=x^4+y^4-z^4+2x^2y^2\)
c) \(C=-\dfrac{1}{4}xy\left(4x^2y^2-x^2y-\dfrac{4}{5}\right)\)
\(C=-\dfrac{1}{4}xy\cdot4x^2y^2+\dfrac{1}{4}xy\cdot x^2y+\dfrac{1}{4}xy\cdot\dfrac{4}{5}\)
\(C=-x^3y^3+\dfrac{1}{4}x^3y^2+\dfrac{1}{5}xy\)
d) \(D=\left(x-y\right)^4\)
\(D=\left[\left(x-y\right)^2\right]^2\)
\(D=\left(x^2-2xy+y^2\right)^2\)
\(D=\left(x^2-2xy+y^2\right)\left(x^2-2xy+y^2\right)\)
\(D=x^4-2x^3y+x^2y^2-2x^3y+4x^2y^2-2xy^3+x^2y^2-2xy^3+y^4\)
\(D=x^4+6x^2y^2+y^4\)
4/
a/ \(A=\dfrac{7y^5z^2-14y^3z^4+2,1y^4z^3}{-7y^3z^2}=\dfrac{7y^5z^2}{-7y^3z^2}+\dfrac{-14y^3z^4}{-7y^3z^2}+\dfrac{2,1y^4z^3}{-7y^3z^2}=-y^2+2z^2-0,3yz\)
b/ \(A=\dfrac{9x^3y+3xy^3-6x^2y^2}{-3xy}=\dfrac{9x^3y}{-3xy}+\dfrac{3xy^3}{-3xy}+\dfrac{-6x^2y^2}{-3xy}=-3x^2-y^2+2xy\)