
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi 2 số đó là A và B
=> A+B=3456
A=4B
=> 5B=3456
Mà 3456 không chia hết 5=> Không tồn tại số tự nhiên B
=> Không tồn tại số tự nhiên A
Vậy ko tồn tại hai số tự nhiên nào mà tổng bằng 3456 và số lớn gấp 4 lần số bé

\(\dfrac{x+2}{-4}=-\dfrac{9}{x+2}\\ \Rightarrow\left(x+2\right)^2=\left(-4\right).\left(-9\right)\\ \Rightarrow\left(x+2\right)^2=36\\ \Rightarrow\left(x+2\right)^2=\pm6^2\\ \Rightarrow\left[{}\begin{matrix}x+2=6\\x+2=-6\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=4\\x=-8\end{matrix}\right.\)

- 27/1=81/3 (Ngược lại)
- 3/9=27/81 (Ngược lại)
- 27/9=3/1 (Ngược lại)
- 81/9=27/3 (Ngược lại)
- 1/27=3/81 (Ngược lại)
\(\dfrac{1}{1}\) = \(\dfrac{3}{3}\) = \(\dfrac{9}{9}\) = \(\dfrac{27}{27}\) = \(\dfrac{81}{81}\)



\(A=\dfrac{1}{2^2}+\dfrac{1}{4^2}+...+\dfrac{1}{100^2}\)
\(=\dfrac{1}{2^2}\left(\dfrac{1}{1}+\dfrac{1}{2^2}+...+\dfrac{1}{50^2}\right)\)
=>\(A< \dfrac{1}{2^2}+\dfrac{1}{2^2}\cdot\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{49}-\dfrac{1}{50}\right)=\dfrac{1}{2^2}+\dfrac{1}{2^2}\cdot\dfrac{49}{50}=\dfrac{99}{200}< \dfrac{1}{2}\)


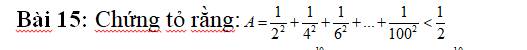

bằng 100
100 nha