Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

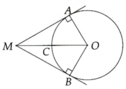
a, Vì MA = MC ( tc tiếp tuyến )
OA = OC = R
Vậy OM là đường trung trực AC hay MO vuông AC
Ta có : ^ACB = 900 ( góc nội tiếp chắn nửa đường tròn )
hay AC vuông BC
lại có AC vuông MO ( cmt )
=> OM // BC ( tc vuông góc đến song song )
b, Vì MA là tiếp tuyến với A là tiếp điểm suy ra ^MAO = 900
Áp dụng định lí Pytago tam giác MAO vuông tại A
\(MO=\sqrt{AM^2+AO^2}=\sqrt{64+36}=10\)cm
Gọi MO giao AC = T
Áp dụng hệ thức : \(AT.MO=AM.AO\Rightarrow AT=\frac{AM.AO}{MO}=\frac{48}{10}=\frac{24}{5}\)cm
Vì MO là đường trung trực nên AT = TC
=> AC = 2AT = 24/5 . 2 = 48/5 cm

a: Xét ΔAOM vuông tại A có \(AM^2+AO^2=OM^2\)
=>\(AM^2=5^2-3^2=16\)
=>\(AM=\sqrt{16}=4\left(cm\right)\)
Xét ΔAOM vuông tại A có \(tanAMO=\dfrac{AO}{AM}\)
=>\(tanAMO=\dfrac{3}{4}\)
b: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là trung trực của AB
=>MO\(\perp\)AB tại I và I là trung điểm của AB
c: Xét (O) có
ΔBDC nội tiếp
BC là đườngkính
Do đó: ΔBDC vuông tại D
=>BD\(\perp\)DC tại D
=>BD\(\perp\)CM tại D
Xét ΔCBM vuông tại B có BD là đường cao
nên \(MD\cdot MC=MB^2\left(3\right)\)
Xét ΔMBO vuông tại B có BI là đường cao
nên \(MI\cdot MO=MB^2\left(4\right)\)
Từ (3) và (4) suy ra \(MD\cdot MC=MI\cdot MO\)
=>\(\dfrac{MD}{MI}=\dfrac{MO}{MC}\)
Xét ΔMDO và ΔMIC có
\(\dfrac{MD}{MI}=\dfrac{MO}{MC}\)
\(\widehat{DMO}\) chung
Do đó: ΔMDO đồng dạng với ΔMIC