K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MH
1
AH
Akai Haruma
Giáo viên
15 tháng 12 2022
Bạn nên tách lẻ các bài ra post riêng. Đăng thế này chiếm diện tích, khó quan sát => mọi người dễ bỏ qua bài của bạn.
19 tháng 1 2023
Bài 2:
a: Gọi (d): y=ax+b là phương trìnhđường thẳng cần tìm
Vì (d) đi qua A(1;-2) và B(2;1) nên ta có hệ:
a+b=-2 và 2a+b=1
=>a=3 và b=-5
b: Gọi (d): y=ax+b là phương trìnhđường thẳng cần tìm
Vì (d) có hệ số góc là 2 nên a=2
=>y=2x+b
Thay x=1 và y=5 vào (d), ta được:
b+2=5
=>b=3
c: Gọi (d): y=ax+b là phương trìnhđường thẳng cần tìm
Vì (d)//y=4x+3
nên a=4
=>y=4x+b
Thay x=-1 và y=8 vào (d), ta được:
b-4=8
=>b=12
d: Gọi (d): y=ax+b là phương trìnhđường thẳng cần tìm
Vì (d)//y=-x+5
nên a=-1
=>y=-x+b
Thay x=2 và y=0 vào (d), ta được:
b-2=0
=>b=2
NT
0
18 tháng 6 2016
a=b(mod n) là công thức dùng để chỉ a,b có cùng số dư khi chia cho n, gọi là đồng dư thức
Ta có các tính chất cua đồng dư thức và các tính chất sau:
Cho x là số tự nhiên
Nếu x lẻ thì => x^2 =1 (mod 8)
x^2 =-1(mod 5) hoặc x^2=0(mod 5)
Nếu x chẵn thì x^2=-1(mod 5) hoặc x^2 =1(mod 5) hoặc x^2=0(mod 5)
Vì 2a +1 và 3a+1 là số chính phương nên ta đặt
3a+1=m^2
2a+1 =n^2
=> m^2 -n^2 =a (1)
m^2 + n^2 =5a +2 (2)
3n^2 -2m^2=1(rút a ra từ 2 pt rồi cho = nhau) (3)
Từ (2) ta có (m^2 + n^2 )=2(mod 5)
Kết hợp với tính chất ở trên ta => m^2=1(mod 5); n^2=1(mod 5)
=> m^2-n^2 =0(mod 5) hay a chia hết cho 5
từ pt ban đầu => n lẻ =>n^2=1(mod 8)
=> 3n^2=3(mod 8)
=> 3n^2 -1 = 2(mod 8)
=> (3n^2 -1)/2 =1(mod 8)
Từ (3) => m^2 = (3n^2 -1)/2
do đó m^2 = 1(mod 8)
ma n^2=1(mod 8)
=> m^2 - n^2 =0 (mod 8)
=> a chia hết cho 8
Ta có a chia hết cho 8 và 5 và 5,8 nguyên tố cùng nhau nên a chia hết cho 40.Vậy a là bội của 40
HP
28 tháng 8 2021
\(x=\sqrt{9+4\sqrt{5}}-\sqrt{9-4\sqrt{5}}\)
\(=\sqrt{\left(\sqrt{5}+2\right)^2}-\sqrt{\left(\sqrt{5}-2\right)^2}\)
\(=\left|\sqrt{5}+2\right|-\left|\sqrt{5}-2\right|\)
\(=\sqrt{5}+2-\sqrt{5}+2=4\)
\(y=\sqrt{3+2\sqrt{5}}-\sqrt{3-2\sqrt{5}}\)
Xem lại đề, \(\sqrt{3-2\sqrt{5}}\) không xác định.
TN
1
LT
0
BL
0
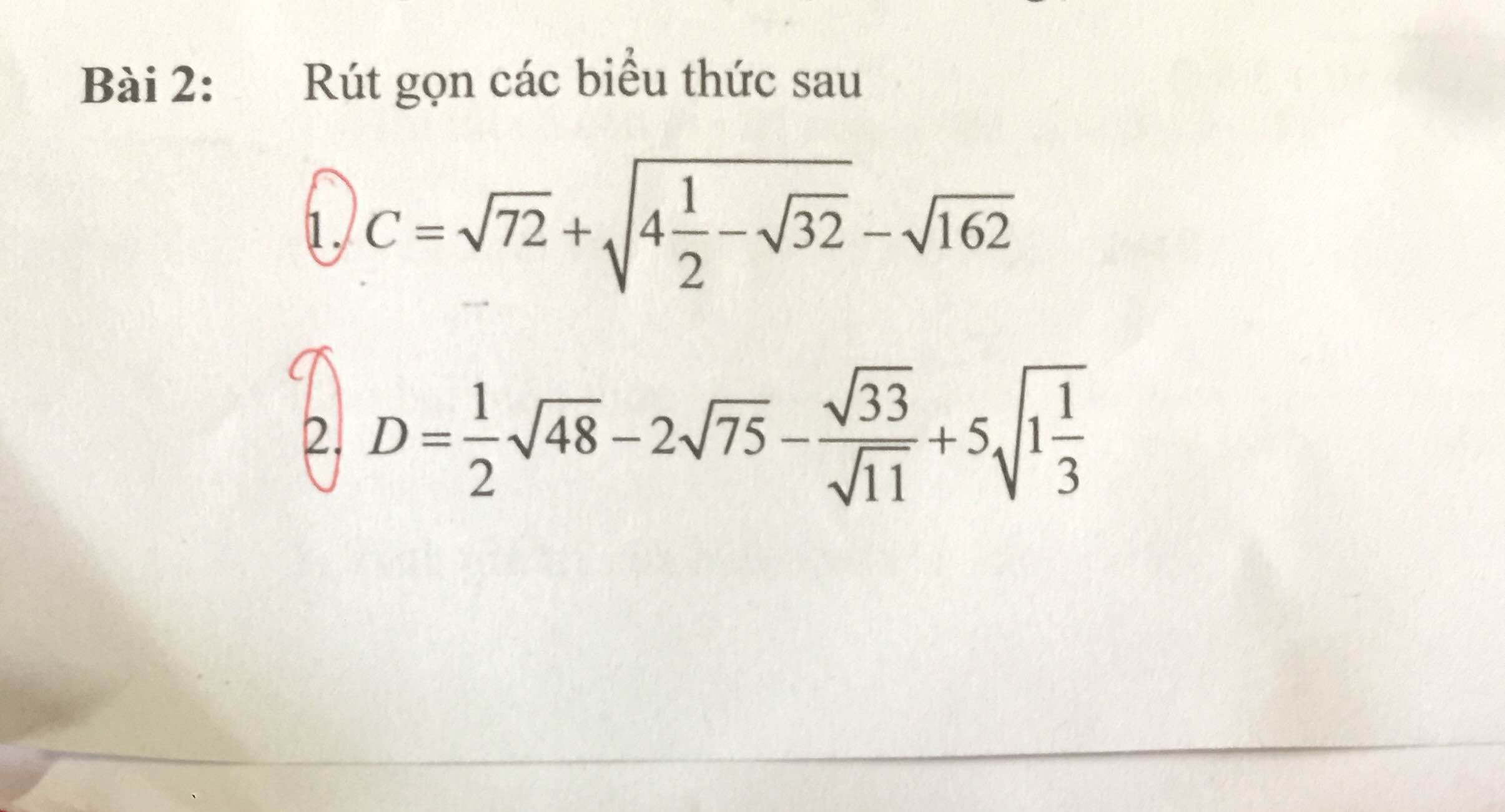
a: Xét (O) có
ΔAIB nội tiếp
AB là đường kính
=>ΔAIB vuông tại I
Xét ΔBAE có
BI vừa là đường cao, vừa là phân giác
nên ΔBAE cân tại B
b: Xét (O) có
ΔACB nội tiếp
AB là đường kính
=>ΔBCA vuông tại C
Xét ΔEAB co
BI.AC là các đường cao
BI cắt AC tại K
=>K là trực tâm
=>EK vuông góc với AB