Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot10=6\cdot8=48\)
hay AH=4,8(cm)

\(1,ĐK:x\ge2\\ PT\Leftrightarrow\sqrt{3x-6}+x-2-\left(\sqrt{2x-3}-1\right)=0\\ \Leftrightarrow\dfrac{3\left(x-2\right)}{\sqrt{3x-6}}+\left(x-2\right)-\dfrac{2\left(x-2\right)}{\sqrt{2x-3}+1}=0\\ \Leftrightarrow\left(x-2\right)\left(\dfrac{3}{\sqrt{3x-6}}-\dfrac{2}{\sqrt{2x-3}+1}+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\\dfrac{3}{\sqrt{3x-6}}-\dfrac{2}{\sqrt{2x-3}+1}+1=0\left(1\right)\end{matrix}\right.\)
Với \(x>2\Leftrightarrow-\dfrac{2}{\sqrt{2x-3}+1}>-\dfrac{2}{1+1}=-1\left(3x-6\ne0\right)\)
\(\Leftrightarrow\left(1\right)>0-1+1=0\left(vn\right)\)
Vậy \(x=2\)
\(2,ĐK:x\ge-1\)
Đặt \(\left\{{}\begin{matrix}\sqrt{x+1}=a\\\sqrt{x^2-x+1}=b\end{matrix}\right.\left(a,b\ge0\right)\Leftrightarrow a^2+b^2=x^2+2\)
\(PT\Leftrightarrow2a^2+2b^2-5ab=0\\ \Leftrightarrow\left(a-2b\right)\left(2a-b\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}a=2b\\b=2a\end{matrix}\right.\)
Với \(a=2b\Leftrightarrow x+1=4x^2-4x+4\left(vn\right)\)
Với \(b=2a\Leftrightarrow4x+4=x^2-x+1\Leftrightarrow x^2-5x-3=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5+\sqrt{37}}{2}\left(tm\right)\\x=\dfrac{5-\sqrt{37}}{2}\left(tm\right)\end{matrix}\right.\)
Vậy ...


1) Vì x=25 thỏa mãn ĐKXĐ nên Thay x=25 vào biểu thức \(A=\dfrac{\sqrt{x}-2}{x+1}\), ta được:
\(A=\dfrac{\sqrt{25}-2}{25+1}=\dfrac{5-2}{25+1}=\dfrac{3}{26}\)
Vậy: Khi x=25 thì \(A=\dfrac{3}{26}\)
2) Ta có: \(B=\dfrac{\sqrt{x}-3}{\sqrt{x}+1}+\dfrac{2x+8\sqrt{x}-6}{x-\sqrt{x}-2}\)
\(=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-5\sqrt{x}+6+2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3x+3\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}}{\sqrt{x}-2}\)

\(x=\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\)
\(\Rightarrow x^3=9+4\sqrt{5}+9-4\sqrt{5}+3\sqrt[3]{\left(9+4\sqrt[]{5}\right)\left(9-4\sqrt{5}\right)}\left(\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\right)\)
\(=18+3\sqrt{81-80}.x=18+3x\)\(\Rightarrow x^3-3x=18\left(1\right)\)
\(y=\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\)
\(\Rightarrow y^3=3+2\sqrt{2}+3-2\sqrt{2}+3\sqrt[3]{\left(3+2\sqrt{2}\right)\left(3-2\sqrt{2}\right)}\left(\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\right)\)
\(=6+3\sqrt[3]{9-8}.y=6+3y\)\(\Rightarrow y^3-3y=6\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow P=x^3+y^3-3\left(x+y\right)+1996=x^3-3x+y^3-3y+1996\)
\(=18+6+1996=2020\)

Bài 3:
a: Gọi OK là khoảng cách từ O đến AB
Suy ra: K là trung điểm của AB
hay \(AK=BK=\dfrac{AB}{2}=\dfrac{8}{2}=4\left(cm\right)\)
Áp dụng định lí Pytago vào ΔOKA vuông tại K, ta được:
\(OA^2=OK^2+KA^2\)
hay OK=3(cm)

a: Ta có: BC⊥BA tại B
nên BC là tiếp tuyến của (A;AB)
b: Xét (A) có
CB là tiếp tuyến
CD là tiếp tuyến
Do đó: CB=CD
hay C nằm trên đường trung trực của BD(1)
Ta có: AB=AD
nên A nằm trên đường trung trực của BD(2)
Từ (1) và (2) suy ra AC là đường trung trực của BD
hay AC\(\perp\)BD
Giúp mình luôn câu c d được không:((( sắp hết h rồi mà không bt làm


8.31:
a: Xét ΔABD có AM/AB=AQ/AD
nên MQ//BD và MQ=BD/2
Xét ΔCBD có CN/CB=CP/CD
nên NP//BD và NP=BD/2
=>MQ//NP và MQ=NP
XétΔBAC có BM/BA=BN/BC
nên MN//AC
=>MN vuông góc BD
=>MN vuông góc MQ
Xét tứ giác MNPQ có
MQ//NP
MQ=NP
góc NMQ=90 độ
=>MNPQ là hình chữ nhật
=>M,N,P,Q cùng nằm trên 1 đường tròn




 Mn giúp mình bài 3 với ạ. Mình đang cần gấp lắm. Mình cảm ơn nhiều !
Mn giúp mình bài 3 với ạ. Mình đang cần gấp lắm. Mình cảm ơn nhiều !

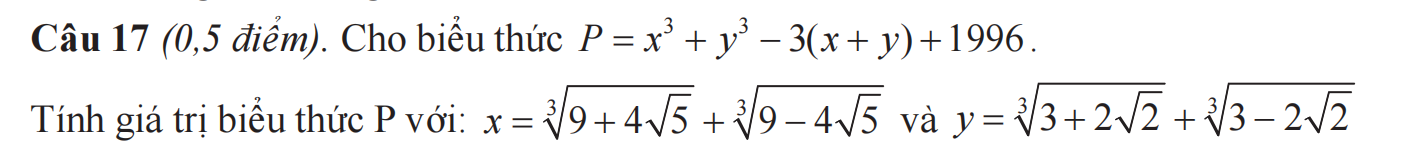 cảm ơn
cảm ơn  , mình đang cần giải gấp. Cảm ơn mn nhiều.
, mình đang cần giải gấp. Cảm ơn mn nhiều.

