Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

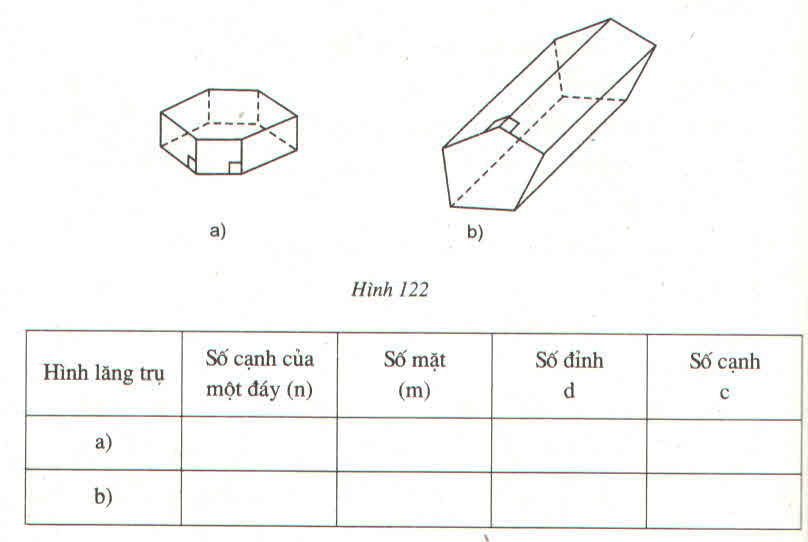
| Hình lăng trụ | SỐ cạnh của một đáy | Số mặt | SỐ đỉnh | SỐ cạnh |
| a | 6 | 8 | 12 | 18 |
| b | 5 | 7 | 10 | 15 |
a: m=n+2
d=2n;
c=3n
b: Số cạnh của một đáy là:
n=d/2=20/2=10(cạnh)
c: Hình lăng trụ có 20 đỉnh thì
Số mặt là m=n+2=10+2=12(mặt)
Số cạnh là c=3n=30(cạnh)
d: Không thể làm một hình lăng trụ có 15 đỉnh bởi 15 là số lẻ

Câu 20:
Ta có: \(\widehat{A}-\widehat{B}=40^0\Rightarrow\widehat{B}=\widehat{A}-40^0\)
\(\widehat{A}=2\widehat{C}\Rightarrow\widehat{C}=\frac{\widehat{A}}{2}\)
Vì AB//CD (gt) \(\Rightarrow\widehat{A}+\widehat{D}=180^0\)(hai góc trong cùng phía)\(\Rightarrow\widehat{D}=180^0-\widehat{A}\)
Tứ giác ABCD \(\Rightarrow\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\Rightarrow\widehat{A}+\left(\widehat{A}-40^0\right)+\frac{\widehat{A}}{2}+\left(180^0-\widehat{A}\right)=360^0\)
Và đến đây bạn dễ dàng tìm được góc A và từ đó suy ra được góc D.
Câu 29: Ta có:
\(\hept{\begin{cases}xy+x+y=3\\yz+y+z=8\\xz+x+z=15\end{cases}}\Leftrightarrow\hept{\begin{cases}xy+x+y+1=4\\yz+y+z+1=9\\xz+x+z+1=16\end{cases}\Leftrightarrow}\hept{\begin{cases}x\left(y+1\right)+\left(y+1\right)=4\\y\left(z+1\right)+\left(z+1\right)=9\\x\left(z+1\right)+\left(z+1\right)=16\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\left(x+1\right)\left(y+1\right)=4\\\left(y+1\right)\left(z+1\right)=9\\\left(z+1\right)\left(x+1\right)=16\end{cases}}\)
Đặt \(\hept{\begin{cases}x+1=a\\y+1=b\\z+1=c\end{cases}}\)với a,b,c > 1, khi đó ta có
\(\hept{\begin{cases}ab=4\\bc=9\\ca=16\end{cases}}\Leftrightarrow\hept{\begin{cases}abbc=4.9\\c=\frac{9}{b}\\ca=16\end{cases}}\Leftrightarrow\hept{\begin{cases}16b^2=36\\c=\frac{9}{b}\\a=\frac{16}{c}\end{cases}}\Leftrightarrow\hept{\begin{cases}b^2=\frac{36}{16}=\frac{9}{4}\\c=\frac{9}{b}\\a=\frac{16}{c}\end{cases}}\Leftrightarrow\hept{\begin{cases}b=\frac{3}{2}\\c=\frac{9}{\frac{3}{2}}=6\\a=\frac{16}{6}=\frac{8}{3}\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x=a-1=\frac{8}{3}-1=\frac{5}{3}\\y=b-1=\frac{3}{2}-1=\frac{1}{2}\\z=c-1=6-1=5\end{cases}}\)
Vậy \(P=x+y+z=\frac{5}{3}+\frac{1}{2}+5=\frac{10+3+30}{6}=\frac{43}{6}\)

Dấu bằng xảy ra khi đẳng thức VT = VP biện luận để tìm ra bài này chắc là tam giác đều
Nguyễn Ngọc Lộc THẾ BẠN CÓ GIẢI ĐƯỢC KHÔNG , mình cần cách giải và cần biết tại sao để tìm duduwowcj dấu bằng ạ

86.NHỮNG PHÉP TÍNH THÚ VỊ
24+36=1
11+13=1
158+207=1
46+54=1
thì khi đó người làm câu hỏi bị sai/ mình nghĩ thế








Lời giải:
$n$ giác có nghĩa là n cạnh. Hình lăng trụ có đáy là đa giác n cạnh. Ở đây, n có hàm ý đại diện cho 1 số như 3 (tam giác), 4 (tứ giác),.....
Bạn vẽ thử 1 hình lăng trụ đứng có n cạnh ra (cho n=3) chả hạn. Khi đó, tương ứng với n cạnh của đáy ta sẽ có n mặt bên. Thêm vào đó có 2 mặt đáy, nên tổng cộng có n+2 mặt.
Công thức ở chỗ khoanh màu cam chỉ là công thức người ta xây dựng nên để áp dụng cho nhanh. Như kiểu công thức diện tích, công thức chu vi thôi.
Trong TH làm bài, bạn chỉ cần vẽ thử 1 lăng trụ đứng (có đáy là tam giác chả hạn) rồi đếm. Đếm TH riêng thì cũng sẽ suy ra TH chung thôi.
Em cảm ơn chị ạ !