
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tham khảo: (Chúc em học giỏi =)
b)Giá trị (x) 5 7 8 9 10 14
Tần số (n) 4 3 8 8 4 3 N= 30
Nhận xét:
- Có 30 giá trị. Có 6 giá trị khác nhau
- Chỉ có 4 học sinh làm được bài nhanh nhất: 5 phút
- Có đến 3 học sinh làm được bài chậm nhất: 14 phút
- Số phút học sinh làm được bài thuộc vào khoảng : 8-9 phút
c)Tính Trung bình cộng:
_
X = 4.5+7.3+8.8+9.8+10.4+14.3 / 30= 259:30 = 8,6 phút

Đây bn nhé:
Ta có a/3 = b/8= c/5. Áp dụng tính chất dãy tỉ số bằng nhau ta có:
2a+3b-c/2.3+3.8-5 = 2a+3b-c/6+24-5 = 50/25 = 2
=> a/3 = 2 => a=6
=> b/8 = 2 => b=16
=> c/5 = 2 => c=10
Nhìn ngắn vậy thôi chứ ko sai đâu bn
Chúc bn học tốt^^
\(\dfrac{a}{3}\) = \(\dfrac{b}{8}\) = \(\dfrac{c}{5}\) và 2a + 3b - c = 50
=> \(\dfrac{2a}{6}\) = \(\dfrac{3b}{24}\) = \(\dfrac{c}{5}\) và 2a + 3b - c = 50
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{2a}{6}\) = \(\dfrac{3b}{24}\) = \(\dfrac{c}{5}\) = \(\dfrac{2a+3b-c}{6+24-5}\) = \(\dfrac{50}{25}\) = 2
Vậy:
\(\dfrac{2a}{6}=2\) => \(2a=2.6=12\) => \(a=12:2=6\)
\(\dfrac{3b}{24}=2\) => \(3b=2.24=48\) => \(b=48:3=16\)
\(\dfrac{c}{5}=2\) => \(c=2.5=10\)

cái này dùng phân số trung gian thôi
-313/370 < -313/371 < -314/371
nên -313/370 < -314/371
các câu sau tương tự


\(\frac{1}{2.7}+\frac{1}{7.12}+\frac{1}{12.17}+....+\frac{1}{2012.2017}\)
\(=\frac{1}{5}\left(\frac{5}{2.7}+\frac{5}{7.12}+\frac{5}{12.17}+....+\frac{5}{2012.2017}\right)\)
\(=\frac{1}{5}\left(\frac{1}{2}-\frac{1}{7}+\frac{1}{7}-\frac{1}{12}+....+\frac{1}{2012}-\frac{1}{2017}\right)\)
\(=\frac{1}{5}\left(\frac{1}{2}-\frac{1}{2017}\right)\)
\(=\frac{1}{5}.\frac{2015}{4034}=\frac{403}{4034}\)
ĐẶT A=DÃY SỐ TRÊN=>5A=5/2.7+........+5/2012.2017
=>A=1/2-1/7........-1/2012-1/2017 RÚT GỌN TA ĐƯỢC A=1/2-1/2017

\(x^2+2y^2-2xy+4y+3< 0\)
\(\Rightarrow x^2-2xy+y^2+y^2+4y+4-1< 0\)
\(\Rightarrow\left(x^2-2xy+y^2\right)+\left(y^2+4y+4\right)-1< 0\)
\(\Rightarrow\left(x-y\right)^2+\left(y+2\right)^2-1< 0\)
Mà: \(\left\{{}\begin{matrix}\left(x-y\right)^2\ge0\forall x,y\\\left(y+2\right)^2\ge0\forall y\end{matrix}\right.\)
\(\Rightarrow\left(x-y\right)^2+\left(y+2\right)^2-1\ge-1\forall x,y\)
Mặt khác: \(\left(x-y\right)^2+\left(y+2\right)^2-1< 0\)
Dấu "=" xảy ra:
\(\left\{{}\begin{matrix}x-y=0\\y+2=0\end{matrix}\right.\)
\(\Rightarrow x=y=-2\)
Vậy: ....

Ta đã biết với mọi x,y \(\inℚ\)thì \(\left|x+y\right|\le\left|x\right|+\left|y\right|\)
Đẳng thức xảy ra khi \(xy\ge0\)
Ta có : \(P=\left|x-2015\right|+\left|x-2016\right|=\left|x-2015\right|+\left|2016-x\right|\ge\left|x-2015+2016-x\right|=\left|1\right|=1\)
Vậy \(P\ge1\), P đạt giá trị nhỏ nhất là 1 khi \(2016\le x\le2015\)


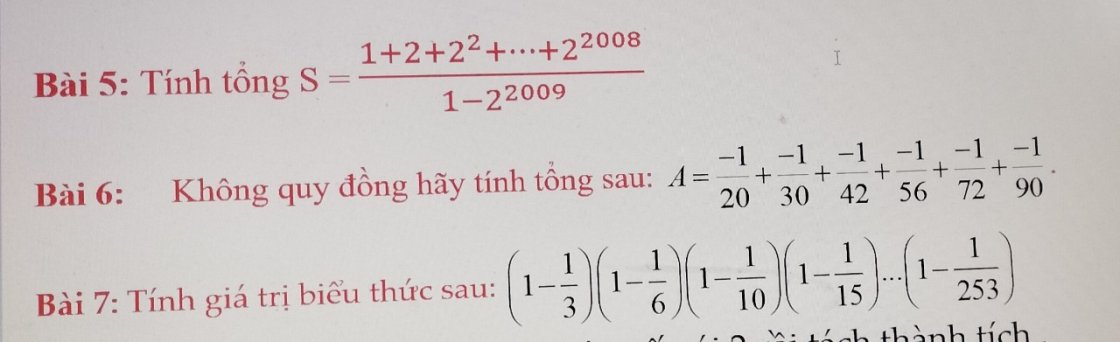 các anh chị giải giúp em bài này đc ko ạ em đang cần gấp nắm
các anh chị giải giúp em bài này đc ko ạ em đang cần gấp nắm
Câu 3 :
\(P=2x.\left(x+y-1\right)+y^2+1\)
\(\Rightarrow P=2x^2+2xy-2x+y^2+1\)
\(\Leftrightarrow P=x^2+2xy+y^2+x^2-2x+1\)
\(\Leftrightarrow P=\left(x+y\right)^2+\left(x-1\right)^2\)
Thay \(x=-5,y=3\) vào \(P=\left(x+y\right)^2+\left(x-1\right)^2\) ta được :
\(P=\left(-5+3\right)^2+\left(-5-1\right)^2=\left(-2\right)^2+\left(-6\right)^2\)
\(=4+36=40\)
Vậy : \(P=40\) tại \(x=-5,y=3\)
b) Ta có : \(P=\left(x+y\right)^2+\left(x-1\right)^2\)
Nhận xét : \(\left(x+y\right)^2\ge0\forall x,y\) ; \(\left(x-1\right)^2\ge0\forall x\)
\(\Leftrightarrow P=\left(x+y\right)^2+\left(x-1\right)^2\ge0\forall x,y\)
hay : \(P\) luôn nhận giá trị dương với mọi \(x,y\). ( đpcm )
Câu 6:
a) Ta có: \(A\left(x\right)+B\left(x\right)=\left(-x^3-5x^2+7x+2\right)+\left(x^3+6x^2-3x-7\right)\)
\(A\left(x\right)+B\left(x\right)=-x^3-5x^2+7x+2+x^3+6x^2-3x-7\)
\(A\left(x\right)+B\left(x\right)=\left(-x^3+x^3\right)+\left(-5x^2+6x^2\right)+\left(7x-3x\right)+\left(2-7\right)\)
\(A\left(x\right)+B\left(x\right)=x^2+4x-5.\)
\(A\left(x\right)-B\left(x\right)=\left(-x^3-5x^2+7x+2\right)-\left(x^3+6x^2-3x-7\right)\)
\(A\left(x\right)-B\left(x\right)=-x^3-5x^2+7x+2-x^3-6x^2+3x+7\)
\(A\left(x\right)-B\left(x\right)=\left(-x^3-x^3\right)+\left(-5x^2-6x^2\right)+\left(7x+3x\right)+\left(2+7\right)\)
\(A\left(x\right)-B\left(x\right)=-2x^3-11x^2+10x+9.\)
b) Thay \(x=1\) vào \(A\left(x\right)+B\left(x\right)\) , ta được:
\(A\left(x\right)+B\left(x\right)=1^2+4.1-5\)
\(A\left(x\right)+B\left(x\right)=1+4-5\)
\(A\left(x\right)+B\left(x\right)=5-5\)
\(A\left(x\right)+B\left(x\right)=0\)
Vậy \(x=1\) là nghiệm của \(A\left(x\right)+B\left(x\right).\)
+ Thay \(x=1\) vào đa thức \(A\left(x\right)\), ta được:
\(A\left(x\right)=\left(-1\right)^3-5.1^2+7.1+2\)
\(A\left(x\right)=\left(-1\right)-5+7+2\)
\(A\left(x\right)=1+2\)
\(A\left(x\right)=3\)
Vậy \(x=1\) không phải là nghiệm của đa thức \(A\left(x\right).\)
Chúc bạn học tốt!