K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CB
1
22 tháng 12 2016
\(GTNN=\frac{1}{2}\left(17-\sqrt{67}\right)\Leftrightarrow x=\frac{7}{3}-\frac{\sqrt{67}}{3}\)
D
20 tháng 1 2022
- SABC=\(\dfrac{1}{2}\)AB.AC=\(\dfrac{1}{2}\).4.6=12(cm2)
- Xét tam giác ABC vuông tại A có:
BC2=AB2+AC2 (định lí Py-ta-go)
=>BC2=42+62=52
=>BC=\(\sqrt{52}\)(cm)
- Xét tam giác ABC có:
AD là đường phân giác của góc A (gt)
=>\(\dfrac{AB}{AC}=\dfrac{BD}{DC}\)(t/c đường phân giác)
=>\(\dfrac{AB+AC}{AC}=\dfrac{BC}{DC}\)
=>\(\dfrac{4+6}{6}=\dfrac{\sqrt{52}}{DC}\)
=>DC=\(\dfrac{6\sqrt{13}}{5}\)
- Ta có: DE vuông góc với AB (gt) ; AC vuông góc với AB (tam giác ABC vuông tại A).
=>DE//AC.
- Xét tam giác ABC có:
DE//AC (cmt)
=>\(\dfrac{AE}{AB}=\dfrac{CD}{BC}\)(định lí Ta-let)
=>\(\dfrac{AE}{4}=\dfrac{\text{}\text{}\dfrac{6\sqrt{13}}{5}}{\sqrt{52}}\)
=>AE=2,4 (cm)
- Ta có: Góc EAF=900(Tam giác ABC vuông tại A)
Góc AED =900(DE vuông góc với AB tại E)
Góc AFD=900(DF vuông góc với AC tại F)
=>DEAF là hình chữ nhật.
Mà AD là phân giác của góc EAF (gt)
=>DEAF là hình vuông.
=>AE=AF=2,4 (cm)
=> SAEF=\(\dfrac{1}{2}\)AE.AF=\(\dfrac{1}{2}\).2,4.2,4=2,88 (cm2)
- SBEFC=SABC-SAEF=12-2,88=9,12 (cm2).
-->Chọn câu A
TA
3
23 tháng 9 2021
\(10,\\ a^2+b^2+c^2+d^2+e^2\ge a\left(b+c+d+e\right)\\ \Leftrightarrow4a^2+4b^2+4c^2+4d^2+4e^2\ge4ab+4ac+4ad+4ae\\ \Leftrightarrow\left(a^2-4ab+4b^2\right)+\left(a^2-4ac+4c^2\right)+\left(a^2-4ad+4d^2\right)+\left(a^2-4ae+4e^2\right)\ge0\\ \Leftrightarrow\left(a-2b\right)^2+\left(a-2c\right)^2+\left(a-2d\right)^2+\left(a-2e\right)^2\ge0\left(luôn.đúng\right)\)
Dấu \("="\Leftrightarrow\dfrac{a}{2}=b=c=d=e\)
23 tháng 9 2021
\(4,\Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ac-\dfrac{1}{4}\left(2a^2+2b^2+2c^2-2ab-2ac-2bc\right)\ge3ab+3bc+3ca\\ \Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ac-\dfrac{1}{2}a^2-\dfrac{1}{2}b^2-\dfrac{1}{2}c^2-ab-bc-ac\ge0\\ \Leftrightarrow\dfrac{1}{2}a^2+\dfrac{1}{2}b^2+\dfrac{1}{2}c^2+ab+ac+bc\ge0\\ \Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ac\ge0\\ \Leftrightarrow\left(a+b+c\right)^2\ge0\left(luôn.đúng\right)\)
Dấu \("="\Leftrightarrow a+b+c=0\)
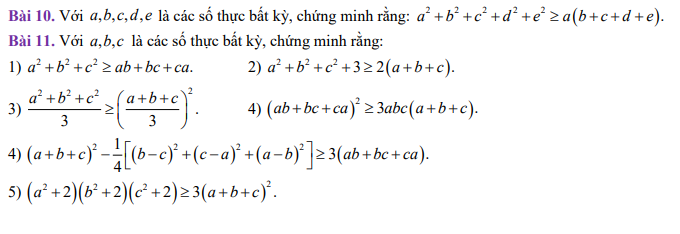
chia buồn với bn nhé
chắc là bài khó quá nên chưa ai làm được