Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A=xy(x+y)-x^2(x+y)+y^2(x+y)
=(x+y)(xy-x^2+y^2)
=x^3+y^3
Thay vào rồi tính típ nha.
B=(2x-1)(2x-1-3+2x)
=(2x-1)(4x-4)
Thay vào rồi tính típ.

\(A=x^2y+xy^2-x^3-x^2y-xy^2+y^3=y^3-x^3=2^3-3^3=8-27=-19\)
\(B=\left(2x-1\right)\left(2x-1-3+2x\right)=4x-4=4\cdot1-4=0\)

Bài 1 :
a, \(A=x^2-4x+6=x^2-4x+4+2=\left(x-2\right)^2+2\ge2\)
Dấu ''='' xảy ra khi x = 2
Vậy GTNN A là 2 khi x = 2
b, \(B=y^2-y+1=y^2-2.\frac{1}{2}y+\frac{1}{4}+\frac{3}{4}=\left(y-\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}\)
Dấu ''='' xảy ra khi y = 1/2
Vậy GTNN B là 3/4 khi y = 1/2
c, \(C=x^2-4x+y^2-y+5=x^2-4x+4+y^2-y+\frac{1}{4}+\frac{3}{4}\)
\(=\left(x-2\right)^2+\left(y-\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}\)
Dấu ''='' xảy ra khi \(x=2;y=\frac{1}{2}\)
Vậy GTNN C là 3/4 khi x = 2 ; y = 1/2
Bài 3 :
a, \(x^2-6x+10=x^2-2.3.x+9+1=\left(x-3\right)^2+1\ge1>0\)( đpcm )
b, \(-y^2+4y-5=-\left(y^2-4y+5\right)=-\left(y^2-4y+4+1\right)=-\left(y-2\right)^2-1< 0\)( đpcm )
Bài 4 :
\(B=\left(x^2+y^2\right)=\left(x+y\right)^2-2xy\)
Thay (*) ta được : \(225-2\left(-100\right)=225+200=425\)
Bài 5 :
\(\left(x+y\right)^2-\left(x-y\right)^2=\left(x+y-x+y\right)\left(x+y+x-y\right)\)
\(=2y.2x=4xy=VP\)( đpcm )

a. A=x(x2-y)-x2(x+y)+y(x2-x)
= x3-xy-x3-x2y+x2y-xy
=-2xy
Với x=1/2, y=-100 A có gt là
-2.1/2.(-100)=100
b. (x2-5)(x+3)+(x+4)(x-x2)
= x3+3x2-5x-15+x2+4x-x3-4x2
=-(x+15)
Với x=-1 gt của B là
-(-1+15)=-14

a, \(A=x^2-y^2-4x\)
\(=\left(x^2-y^2\right)-4x\)
\(=\left(x+y\right)\left(x-y\right)-4x\)
\(=2\left(x-y\right)-2.2x\)
\(=2\left(x-y-2x\right)\)
\(=2\left(-x-y\right)\)
\(=2\left[-\left(x+y\right)\right]\)
\(=-2\left(x+y\right)\)
\(=-2.2=-4\)
Vậy \(A=-4\)
b, \(B=x^2+y^2+2xy-4x-4y-3\)
\(=\left(x^2+2xy+y^2\right)-\left(4x+4y\right)-3\)
\(=\left(x+y\right)^2-4\left(x+y\right)-3\)
\(=4^2-4.4-3\)
\(=-3\)
Vậy \(B=-3\)
c, Phần này hình như đề bài sai, bạn xem lại đề hộ mk cái nhé ;)
A =(x+y)(x-y) -4x = 2(x-y) -4x = 2x -2y - 4x = - 2(x+y) = -4
.............
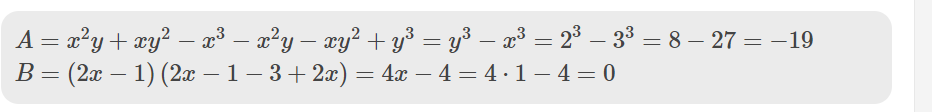
1) Với x = 0; y = 2
A = (x^2 - y^2 + x + y)/(2 + x^2 + y^2)
A = (0^2 - 2^2 + 0 + 2)/(2 + 0^2 + 2^2)
A = -1/3
3) Với x = 2; y = -2
A = (x^2 - y^2 + x + y)/(2 + x^2 + y^2)
A = [2^2 - (-2)^2 + 2 + (-2)]/[2 + 2^2 + (-2)^2]
A = 0