
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(x + y = 1 \Rightarrow y = 1 - x\), vậy với mỗi giá trị x chỉ có 1 giá trị y giá trị y, vậy x=y+1 là hàm số
b) \(y = {x^2}\)là 1 hàm số
c) \({y^2} = x \Rightarrow \)\(y = \sqrt x \)hoặc \(y = - \sqrt x \)(nếu \(x \ge 0\)), vậy 1 giá trị của x lại có 2 giá trị y, nên đây không phải là hàm số
d) \({x^2} - {y^2} = 0 \Leftrightarrow {x^2} = {y^2}\), y=x hoặc y=-x, vậy 1 giá trị của x lại có 2 giá trị y, nên đây không phải là hàm số

Chọn A.
Ta có: A = cos2x.cot2x + 3cos2x - cot2x + 2sin2x
=( cos2x.cot2x - cot2x) + (2sin2x + 2cos2x) + cos2x
= cot2x( cos2x - 1) + 2 + cos2x
= - cot2x. sin2x + 2 + cos2x
= -cos2x + 2 + cos2x = 2

\(A=cos^2x+\dfrac{1+cos\left(\dfrac{2\pi}{3}+2x\right)}{2}+\dfrac{1+cos\left(\dfrac{2\pi}{3}-2x\right)}{2}\\ =cos^2x+1+\dfrac{cos\left(\dfrac{2\pi}{3}+2x\right)+cos\left(\dfrac{2\pi}{3}-2x\right)}{2}\\ =cos^2x+1+cos\left(\dfrac{2\pi}{3}\right).cos2x\\ =cos^2x+1-\dfrac{1}{2}.cos2x=\dfrac{1+cos2x}{2}+1-\dfrac{cos2x}{2}=\dfrac{3}{2}.\)

Sửa đề: sin^4x+cos^4x+1
\(A=\dfrac{\left(sin^2x+cos^2x\right)^3-3sin^2xcos^2x+2}{\left(sin^2x+cos^2x\right)^2-2sin^2xcos^2x+1}\)
\(=\dfrac{3\left(1-sin^2xcos^2x\right)}{2\left(1-sin^2xcos^2x\right)}=\dfrac{3}{2}\)

\(P=\dfrac{\left(cos^2x-sin^2x\right)^2}{4sin^2x.cos^2x}-\dfrac{1}{4sin^2x.cos^2x}=\dfrac{\left(cos^2x-1-sin^2x\right)\left(cos^2x+1-sin^2x\right)}{4sin^2x.cos^2x}\)
\(=\dfrac{-2sin^2x.2cos^2x}{4sin^2x.cos^2x}=-1\)
\(y^2-3y-1=0\) có \(ac=-1< 0\Leftrightarrow\) có 2 nghiệm trái dấu hay có 1 nghiệm dương
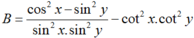
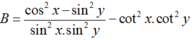
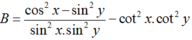
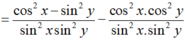
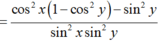
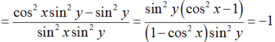
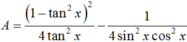
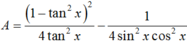
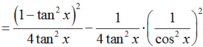
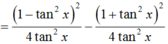
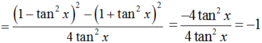
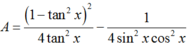
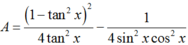
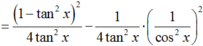
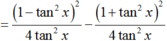
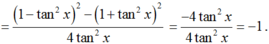
Chọn D.
Ta có