Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bài 2
A B C O H K J
ta có \(\overrightarrow{AO}.\left(\overrightarrow{BO}+\overrightarrow{AC}-2\overrightarrow{BC}\right)=\overrightarrow{AO}.\overrightarrow{BO}+\overrightarrow{AO}.\overrightarrow{AC}-\overrightarrow{AO}.2\overrightarrow{BC}\)
\(=\overrightarrow{AO}.\overrightarrow{BO}+\overrightarrow{AO}.\overrightarrow{AC}=AO.BO.cos\left(120^0\right)+AO.AC.cos\left(30^0\right)\)
\(=\frac{a\sqrt{3}}{3}.\frac{a\sqrt{3}}{3}.-\frac{1}{2}+\frac{a\sqrt{3}}{3}.a.\frac{\sqrt{3}}{2}=\frac{a^2}{3}\)
b.Gọi J là trung điểm CK
ta có \(\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}=2\overrightarrow{MK}+2\overrightarrow{MC}=4\overrightarrow{MJ}\)
do \(\left|4\overrightarrow{MJ}\right|=a\Leftrightarrow MJ=\frac{a}{4}\)vậy tập hợp M là các điểm nằm trên đường tròn tâm J bán kính a/4.
Bài 3. điều kiện \(x\ge1\)
đặt \(\sqrt{x-1}=a\ge0\) ta có
\(a^2+a+3=3\sqrt{a^3+1}\)
hay \(\left(a^2-a+1\right)+2\left(a+1\right)=3\sqrt{\left(a^2-a+1\right).\left(a+1\right)}\)
\(\Leftrightarrow\left(\sqrt{a^2-a+1}-\sqrt{a+1}\right)\left(\sqrt{a^2-a+1}-2\sqrt{a+1}\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}a^2-a+1=a+1\\a^2-a+1=4\left(a+1\right)\end{cases}\Leftrightarrow\orbr{\begin{cases}a=0\\a=2\end{cases}}}\) hoặc \(a=\frac{5+\sqrt{37}}{2}\)
từ đó ta tìm được x thuộc tập \(S=\left\{1;5;\frac{33+5\sqrt{37}}{2}\right\}\)

a) Lấy (1)+(2)+(3) là tìm được z rồi thế z vào tìm x, y
b) Lấy (1) + (2) - (3) là tìm được y
\(a)\hept{\begin{cases}x-2y+z=12\\2x-y+3z=18\\-3x+3y+2z=-9\end{cases}\Leftrightarrow\hept{\begin{cases}x-2y+z=12\\3y+z=-6\\6z=21\end{cases}}}\)
\(\text{Đáp số: }(x;y;z)=(\frac{16}{3};-\frac{19}{6};\frac{7}{2})\)
\(b)\hept{\begin{cases}x+y+z=7\\3x-2y+2z=5\\4x-y+3z=10\end{cases}\Leftrightarrow}\hept{\begin{cases}x+y+z=7\\-5y-z=16\\0y+0z=-2\end{cases}}\)
\(\text{ Hệ phương trình vô nghiệm.}\)

Câu 1.
x2 + 2( m - 3 )x + 1 - m = 0
Để phương trình có nghiệm thì Δ ≥ 0
=> [ 2( m - 3 ) ]2 - 4( 1 - m ) ≥ 0
<=> 4( m - 3 )2 - 4 + 4m ≥ 0
<=> 4( m2 - 6m + 9 ) - 4 + 4m ≥ 0
<=> 4m2 - 24m + 36 - 4 + 4m ≥ 0
<=> 4m2 - 20m + 32 ≥ 0
<=> m2 - 5m + 8 ≥ 0 ( luôn đúng với mọi m )
Vậy phương trình có nghiệm với mọi m


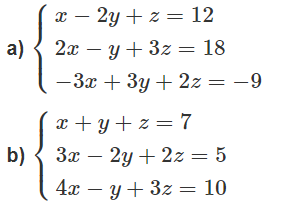 Giúp nhanh vs ạ, đng cần gấp
Giúp nhanh vs ạ, đng cần gấp
Tham khảo hình ảnh!
Không thấy ảnh = ib
Not s.p.a.m!
trả lời:
k cho mik nha
HT