Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi số lớn là x số nhỏ là y(2014>x>y>0)
ta có x+y=2014 và x=y+14<=>x-y=14
ta được bài toán tìm ẩn biết tổng và hiệu của chúng
=>x=(2014+14):2=1014(nhận)
=>y=2014-1014=1000(nhận)
vậy 2 số đó là 1014 và 1000

Gọi số lớn là a, số bé là b
Theo đề bài ta có:
\(\left\{{}\begin{matrix}a+b=2024\\a-b=16\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}a=1020\\b=1004\end{matrix}\right.\)
Vậy hai số tự nhiên đó là 1020 và 1004.
Gọi hai số đó là: \(a,b\)
Tổng của hai số là 2024: \(a+b=2024\)(1)
Hiệu của hai số là 16: \(a-b=16\) (2)
Từ (1) và (2) ta có hệ:
\(\left\{{}\begin{matrix}a+b=2024\\a-b=16\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=2024\\2a=2040\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=2024\\a=\dfrac{2040}{2}=1020\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}1020+b=2024\\a=1020\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=2024-1020=1004\\a=1020\end{matrix}\right.\)
Vậy: ..

Bài 1:
Gọi hai số tự nhiên cần tìm là a,b
Số thứ nhất gấp 4 lần số thứ hai nên a=4b(1)
Tổng của hai số là 100 nên a+b=100(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}a=4b\\a+b=100\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4b+b=100\\a=4b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5b=100\\a=4b\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=\dfrac{100}{5}=20\\a=4\cdot20=80\end{matrix}\right.\)
Bài 2:
Gọi hai số cần tìm là a,b
Hiệu của hai số là 10 nên a-b=10(4)
Hai lần số thứ nhất bằng ba lần số thứ hai nên 2a=3b(3)
Từ (3) và (4) ta có hệ phương trình:
\(\left\{{}\begin{matrix}a-b=10\\2a=3b\end{matrix}\right.\Leftrightarrow\)\(\left\{{}\begin{matrix}a-b=10\\2a-3b=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2a-2b=20\\2a-3b=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2a-2b-2a+3b=20\\2a=3b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=20\\2a=3\cdot20=60\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=30\\b=20\end{matrix}\right.\)
Bài 3:
Gọi số tự nhiên cần tìm có dạng là \(\overline{ab}\left(a\ne0\right)\)
Chữ số hàng chục bé hơn chữ số hàng đơn vị là 3 nên b-a=3(5)
Nếu đổi chỗ hai chữ số cho nhau thì tổng của số mới lập ra và số ban đầu là 77 nên ta có:
\(\overline{ab}+\overline{ba}=77\)
=>\(10a+b+10b+a=77\)
=>11a+11b=77
=>a+b=7(6)
Từ (5) và (6) ta có hệ phương trình:
\(\left\{{}\begin{matrix}-a+b=5\\a+b=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-a+b+a+b=5+7\\a+b=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2b=12\\a+b=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=6\\a=7-6=1\end{matrix}\right.\)
Vậy: Số tự nhiên cần tìm là 16

Gọi hai số cần tìm là a,b
Theo đề, ta có:
a+b=1006 và a=2b+124
=>a+b=1006 và a-2b=124
=>a=712 và b=294

a) Gọi 2 số đó là x và y. (0<x,y<33)
Tổng 2 số là 33: x+y=33 (1)
Tích 2 số là 270: x.y=270 (2)
Từ (1),(2) ta có hpt:
\(\left\{{}\begin{matrix}x+y=33\\x.y=270\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=33-y\\\left(33-y\right).y=270\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=33-y\\-y^2+33y-270=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=33-y\\\left[{}\begin{matrix}y=18\\y=15\end{matrix}\right.\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}y=18\\x=33-18=15\end{matrix}\right.\\\left\{{}\begin{matrix}y=15\\x=33-15=18\end{matrix}\right.\end{matrix}\right.\)
Vậy: Hai số cần tìm là 18 và 15.

Gọi số lớn là x, số nhỏ là y (x, y ∈ N*); x,y > 124.
Tổng hai số bằng 1006 nên ta có: x + y = 1006
Số lớn chia số nhỏ được thương là 2, số dư là 124 nên ta có: x = 2y + 124.
Ta có hệ phương trình:
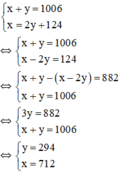
Vậy hai số tự nhiên phải tìm là 712 và 294.
Chú ý : Số bị chia = số chia. thương + số dư

Gọi số lớn là x, số nhỏ là y (x, y ∈ N*); x,y > 124.
Tổng hai số bằng 1006 nên ta có: x + y = 1006
Số lớn chia số nhỏ được thương là 2, số dư là 124 nên ta có: x = 2y + 124.
Ta có hệ phương trình:
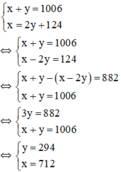
Vậy hai số tự nhiên phải tìm là 712 và 294.
Chú ý : Số bị chia = số chia. thương + số dư
Kiến thức áp dụng
Giải bài toán bằng cách lập hệ phương trình:
Bước 1: Lập hệ phương trình
- Chọn các ẩn số và đặt điều kiện thích hợp
- Biểu diễn các đại lượng chưa biết và đã biết theo ẩn
- Lập các phương trình biểu thị mối quan hệ giữa các đại lượng theo đề bài.
- Từ các phương trình vừa lập rút ra được hệ phương trình.
Bước 2: Giải hệ phương trình (thường sử dụng phương pháp thế hoặc cộng đại số).
Bước 3: Đối chiếu nghiệm với điều kiện và kết luận.

1. ta có abc + deg = 560
abc : deg = 3 dư 68
(1 + 3) x deg = 560- 68 = 492
deg = 492 : 4 = 123
abc là : 123 x 3 + 68 = 437
2. ta có :
ab + ba = 99
ba - ab = 27
ba = ( 99 + 27) : 2 = 63
ab = 99 - 63 = 36
HT

Gọi x là số lớn, y là số bé. ĐK : x>y và 0<x,y<1006
Vì tổng của 2 số này bằng 1006 nên : x+y=1006 (*)
Mà nếu lấy số lớn chia cho số nhỏ thì đc thương là 2 và số dư là 124 nên ta có: x= 2y + 124 .
Thay vào (*) ta đc: y+2y+124 =1006<=>3y = 882=>y=882/3 = 294
=>x=1006-294 =712
Vậy....................
Gọi số lớn là x , số nhỏ là y ( x , y ∈ N* ) ; x > 124.
Vì tổng hai số bằng 1006 nên ta có: x + y = 1006 .
Số lớn chia số nhỏ được thương là 2, số dư là 124 nên ta có: x = 2y + 124.
Ta có hệ phương trình:
Vậy ..........
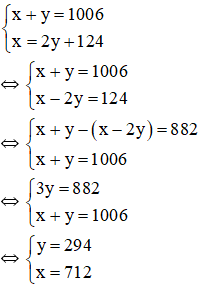
Số bé là:
(56-14):2=21
Số lớn là:
21+14=35