Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
Ta có
![]()
![]()
Đặt t = 2 x > 0 thì phương trình đã cho trở thành t 2 - 2 m . t + m + 2 = 0 *
Để phương trình đã cho có hai nghiệm dương phân biệt khi và chỉ khi phương trình (*) có hai nghiệm t 1 , t 2 lớn hơn 1.
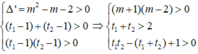
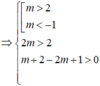
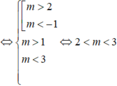
![]()

Đáp án A.
Phương trình đã cho tương đương với:
2 x 2 + m x + 1 = x 2 + 6 x + 9 x ≥ − 3 ⇔ x 2 + m − 6 x − 8 = 0 1 x ≥ − 3
Để phương trình có hai nghiệm phân biệt thì (1) phải có 2 nghiệm phân biệt x 2 > x 1 ≥ − 3
⇔ Δ > 0 x 1 + x 2 ≥ − 6 x 1 + 3 x 2 + 3 ≥ 0 ⇔ m − 6 2 + 32 > 0 − m − 6 ≥ − 6 − 8 + 3. − m + 6 + 9 ≥ 0 ⇔ 6 − m ≥ − 6 19 − 3 m ≥ 0 ⇔ m ≤ 12 m ≤ 19 3 ⇔ m ≤ 19 3
Do đó
a b = 19 3 ⇒ a = 19 b = 3 ⇒ B = a 2 − b 3 = 19 2 − 3 3 = 334.

Đáp án A
Đặt t = 2 x > 0 ⇒ t 2 − 2 m t + m + 2 = 0
ĐK PT có 2 nghiệm phân biệt là: Δ ' = m 2 − m − 2 > 0 S = 2 m > 0 P = m + 2 > 0 ⇔ m > 2
Khi đó: 2 x 1 = t 1 2 x 2 = t 2 ⇒ x 1 = log 2 t 1 ; x 2 = log 2 t 2
Để x 1 ; x 2 > 0 ⇔ t 1 > 1 ; t 2 > 1 ⇔ t 1 + t 2 > 2 t 1 − 1 t 2 − 1 > 0 ⇔ 2 m > 2 m + 2 − 2 m + 1 > 0 ⇔ 1 < m < 3
Vậy m ∈ 2 ; 3

*x2+bx+c=0
\(\Delta=b^2-4c=b^2-4.\left(2b-4\right)=b^2-8b+16=\left(b-4\right)^2\)=>\(\sqrt{\Delta}=\left|b-4\right|\)
Với (b-4)2=0 =>b=4 =>c=4
PT có 1 nghiệm kép: \(x_1=x_2=-2\)
Với\(\Delta=\) (b-4)2>0,PT có 2 nghiệm pb: \(x_1=\frac{-b+\left|b-4\right|}{2};x_2=\frac{-b-\left|b-4\right|}{2}\)
Với b>4 thì: \(x_1=-2;x_2=\frac{-2b+4}{2}=-b+2\)
Với b<0 thì: x1=-b+2 ; x2=-2
Vậy khi c=2b-4 và b tùy ý thì PT: x2+bx+c=0 luôn có 1 nghiệm nguyên là -2

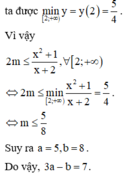





Đáp án A
Ta có 4 sin 2 x + 5 cos 2 x ≤ m . 7 cos 2 x ⇔ 4 1 - cos 2 x + 5 cos 2 x ≤ m . 7 cos 2 x ⇔ m ≥ 4 28 cos 2 x + 5 7 cos 2 x
Đặt t = cos 2 x , 0 ≤ t ≤ 1 khi đó m ≥ 4 28 t + 5 7 t = g t
Phương trình đã cho có nghiệm ⇔ m ≥ m i n 0 ; 1 g t
Dễ thấy g ' t < 0 ∀ t ∈ 0 ; 1 ⇒ m i n 0 ; 1 g t = g 1 = 6 7 ⇒ m ≥ 6 7 là giá trị cần tìm
Vậy a + b + c = 13.