Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án: B
Số tập hợp con chứa α, β của A là: {α, β }; {α, β, γ };{α, β, ε};{α, β, μ };{α, β, γ, ε };{α, β, γ, μ };{α, β, ε, μ };{α, β, γ, ε, μ }
Hai góc α và β phụ nhau nên sin α = cos β ; cos α = sin β .
Do đó, P = cos α cos β − sin β sin α = cos α sin α − cos α sin α = 0 .
Chọn A.
Hai góc α và β bù nhau nên sin α = sin β ; cos α = − cos β .
Do đó P = cos α cos β − sin β sin α = − cos 2 α − sin 2 α = − sin 2 α + cos 2 α = − 1 .
Chọn C.
Hai góc α và β phụ nhau nên sin α = cos β ; cos α = sin β .
Do đó, P = sin α cos β + sin β cos α = sin 2 α + cos 2 α = 1 .
Chọn B.
Chọn C.
Ta có :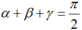 
, suy ra
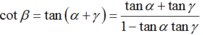
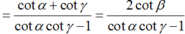
Suy ra :
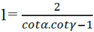( rút gọn cả 2 vế cho cotβ)
⇒ cot α.cot γ =3.
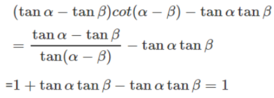
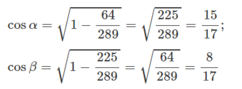
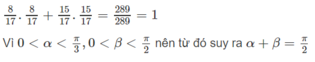
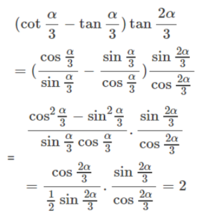
Theo Viet ta có \(\left\{{}\begin{matrix}tana+tanb=p\\tana.tanb=q\end{matrix}\right.\)
\(\Rightarrow tan\left(a+b\right)=\frac{tana+tanb}{1-tana.tanb}=\frac{p}{1-q}\)
\(A=cos^2\left(a+b\right)\left[1+p.tan\left(a+b\right)+q.tan^2\left(a+b\right)\right]\)
\(A=\frac{1}{1+tan^2\left(a+b\right)}\left[1+\frac{p^2}{1-q}+\frac{q.p^2}{\left(1-q\right)^2}\right]\)
\(A=\frac{\left(1-q\right)^2}{p^2+\left(1-q\right)^2}\left(1+\frac{p^2}{\left(1-q^2\right)}\right)\)
\(A=\frac{\left(1-q^2\right)}{p^2+\left(1-q\right)^2}.\left(\frac{p^2+\left(1-q\right)^2}{\left(1-q\right)^2}\right)=1\)