
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

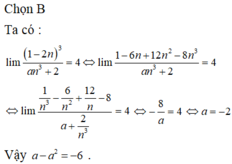

3.
\(x-2y+1=0\Leftrightarrow y=\frac{1}{2}x+\frac{1}{2}\)
\(y'=\frac{2}{\left(x+1\right)^2}\Rightarrow\frac{2}{\left(x+1\right)^2}=\frac{1}{2}\)
\(\Rightarrow\left(x+1\right)^2=4\Rightarrow\left[{}\begin{matrix}x=1\Rightarrow y=1\\x=-3\Rightarrow y=3\end{matrix}\right.\)
Có 2 tiếp tuyến: \(\left[{}\begin{matrix}y=\frac{1}{2}\left(x-1\right)+1\\y=\frac{1}{2}\left(x+3\right)+3\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}y=\frac{1}{2}x+\frac{1}{2}\left(l\right)\\y=\frac{1}{2}x+\frac{9}{2}\end{matrix}\right.\)
4.
\(\lim\limits\frac{\sqrt{2n^2+1}-3n}{n+2}=\lim\limits\frac{\sqrt{2+\frac{1}{n^2}}-3}{1+\frac{2}{n}}=\sqrt{2}-3\)
\(\Rightarrow\left\{{}\begin{matrix}a=2\\b=3\end{matrix}\right.\)
5.
\(\lim\limits_{x\rightarrow a}\frac{2\left(x^2-a^2\right)+a\left(a+1\right)-\left(a+1\right)x}{\left(x-a\right)\left(x+a\right)}=\lim\limits_{x\rightarrow a}\frac{\left(x-a\right)\left(2x+2a\right)-\left(a+1\right)\left(x-a\right)}{\left(x-a\right)\left(x+a\right)}\)
\(=\lim\limits_{x\rightarrow a}\frac{\left(x-a\right)\left(2x+a-1\right)}{\left(x-a\right)\left(x+a\right)}=\lim\limits_{x\rightarrow a}\frac{2x+a-1}{x+a}=\frac{3a-1}{2a}\)
1.
\(f'\left(x\right)=-3x^2+6mx-12=3\left(-x^2+2mx-4\right)=3g\left(x\right)\)
Để \(f'\left(x\right)\le0\) \(\forall x\in R\) \(\Leftrightarrow g\left(x\right)\le0;\forall x\in R\)
\(\Leftrightarrow\Delta'=m^2-4\le0\Rightarrow-2\le m\le2\)
\(\Rightarrow m=\left\{-1;0;1;2\right\}\)
2.
\(f'\left(x\right)=\frac{m^2-20}{\left(2x+m\right)^2}\)
Để \(f'\left(x\right)< 0;\forall x\in\left(0;2\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-20< 0\\\left[{}\begin{matrix}m>0\\m< -4\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}-\sqrt{20}< m< \sqrt{20}\\\left[{}\begin{matrix}m>0\\m< -4\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow m=\left\{1;2;3;4\right\}\)

\(y'=4x^3-4mx\Rightarrow y'\left(1\right)=4-4m\)
\(A\left(1;1-m\right)\)
Phương trình tiếp tuyến d tại A có dạng:
\(y=\left(4-4m\right)\left(x-1\right)+1-m\)
\(\Leftrightarrow\left(4-4m\right)x-y+3m-3=0\)
\(d\left(B;d\right)=\dfrac{\left|\dfrac{3}{4}\left(4-4m\right)-1+3m-3\right|}{\sqrt{\left(4-4m\right)^2+1}}=\dfrac{1}{\sqrt{\left(4-4m\right)^2+1}}\le1\)
Dấu "=" xảy ra khi và chỉ khi \(4-4m=0\Rightarrow m=1\)
y′=4x3−4mx⇒y′(1)=4−4my′=4x3−4mx⇒y′(1)=4−4m
A(1;1−m)A(1;1−m)
Phương trình tiếp tuyến d tại A có dạng:
y=(4−4m)(x−1)+1−my=(4−4m)(x−1)+1−m
⇔(4−4m)x−y+3m−3=0⇔(4−4m)x−y+3m−3=0
d(B;d)=∣∣∣34(4−4m)−1+3m−3∣∣∣√(4−4m)2+1=1√(4−4m)2+1≤1d(B;d)=|34(4−4m)−1+3m−3|(4−4m)2+1=1(4−4m)2+1≤1
Dấu "=" xảy ra khi và chỉ khi 4−4m=0⇒m=1

25.
H là hình chiếu của S lên (ABC)
Do \(SA=SB=SC\Rightarrow HA=HB=HC\)
\(\Rightarrow\) H là tâm đường tròn ngoại tiếp tam giác ABC
26.
\(\left\{{}\begin{matrix}AB\perp BC\\AB\perp CD\end{matrix}\right.\) \(\Rightarrow AB\perp\left(BCD\right)\) \(\Rightarrow AB\perp BD\)
\(\Rightarrow\Delta ABD\) vuông tại B
Pitago tam giác vuông BCD (vuông tại C):
\(BC^2+CD^2=BD^2\Rightarrow BD^2=b^2+c^2\)
Pitago tam giác vuông ABD:
\(AD^2=AB^2+BC^2=a^2+b^2+c^2\)
\(\Rightarrow AD=\sqrt{a^2+b^2+c^2}\)
23.
Gọi H là chân đường cao hạ từ S xuống BC
\(\Rightarrow BH=SB.cos30^0=3a\) ; \(SH=SB.sin30^0=a\sqrt{3}\) ; \(CH=4a-3a=a\)
\(\Rightarrow BC=4HC\Rightarrow d\left(B;\left(SAC\right)\right)=4d\left(H;\left(SAC\right)\right)\)
Từ H kẻ \(HE\perp AC\) ; từ H kẻ \(HF\perp SE\Rightarrow HF\perp\left(SAC\right)\)
\(\Rightarrow HF=d\left(H;\left(SAC\right)\right)\)
\(HE=CH.sinC=\frac{CH.AB}{AC}=\frac{a.3a}{5a}=\frac{3a}{5}\)
\(\frac{1}{HF^2}=\frac{1}{HE^2}+\frac{1}{SH^2}\Rightarrow HF=\frac{HE.SH}{\sqrt{HE^2+SH^2}}=\frac{3a\sqrt{7}}{14}\)
\(\Rightarrow d\left(B;\left(SAC\right)\right)=4HF=\frac{6a\sqrt{7}}{7}\)
24.
\(SA=SC\Rightarrow SO\perp AC\)
\(SB=SD\Rightarrow SO\perp BD\)
\(\Rightarrow SO\perp\left(ABCD\right)\)

1.
\(\lim\dfrac{5\sqrt{3n^2+n}}{2\left(3n+2\right)}=\lim\dfrac{5\sqrt{3+\dfrac{1}{n}}}{2\left(3+\dfrac{2}{n}\right)}=\dfrac{5\sqrt{3}}{6}\Rightarrow a+b=11\)
2.
\(\lim\limits_{x\rightarrow2}\dfrac{x^2+ax+b}{x-2}=6\) khi \(x^2+ax+b=0\) có nghiệm \(x=2\)
\(\Rightarrow4+2a+b=0\Rightarrow b=-2a-4\)
\(\lim\limits_{x\rightarrow2}\dfrac{x^2+ax-2a-4}{x-2}=\lim\limits_{x\rightarrow2}\dfrac{\left(x-2\right)\left(x+2\right)+a\left(x-2\right)}{x-2}=\lim\limits_{x\rightarrow2}\dfrac{\left(x-2\right)\left(x+a+2\right)}{x-2}\)
\(=\lim\limits_{x\rightarrow2}\left(x+a+2\right)=a+4\Rightarrow a+4=6\Rightarrow a=2\Rightarrow b=-8\)
\(\Rightarrow a+b=-6\)