Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Số hạng thứ \(k+1\) của khai triển là :
\(t_{k+1}=C^k_n\left(3x\right)^k\)
Vậy số hạng chứa \(x^2\) là \(t_3=C^2_n9.x^2\)
Theo đề bài ta có :
\(9.C^2_n=90\Leftrightarrow C^2_n=10\Leftrightarrow n=5\)
\(\left(x^{-4}+x^{\frac{5}{2}}\right)^{12}\) có SHTQ: \(C_{12}^kx^{-4k}.x^{\frac{5}{2}\left(12-k\right)}=C^k_{12}x^{30-\frac{13}{2}k}\)
Số hạng chứa \(x^8\Rightarrow30-\frac{13}{2}k=8\Rightarrow\) ko có k nguyên thỏa mãn
Vậy trong khai triển trên ko có số hạng chứa \(x^8\)
b/ \(\left(1-x^2+x^4\right)^{16}\)
\(\left\{{}\begin{matrix}k_0+k_2+k_4=16\\2k_2+4k_4=16\end{matrix}\right.\)
\(\Rightarrow\left(k_0;k_2;k_4\right)=\left(8;8;0\right);\left(9;6;1\right);\left(10;4;2\right);\left(11;2;3\right);\left(12;0;4\right)\)
Hệ số của số hạng chứa \(x^{16}\):
\(\frac{16!}{8!.8!}+\frac{16!}{9!.6!}+\frac{16!}{10!.4!.2!}+\frac{16!}{11!.2!.3!}+\frac{16!}{12!.4!}=...\)
c/ SHTQ của khai triển \(\left(1-2x\right)^5\) là \(C_5^k\left(-2\right)^kx^k\)
Số hạng chứa \(x^4\) có hệ số: \(C_5^4.\left(-2\right)^4\)
SHTQ của khai triển \(\left(1+3x\right)^{10}\) là: \(C_{10}^k3^kx^k\)
Số hạng chứa \(x^3\) có hệ số \(C_{10}^33^3\)
\(\Rightarrow\) Hệ số của số hạng chứa \(x^5\) là: \(C_5^4\left(-2\right)^4+C_{10}^3.3^3\)
Số hạng tổng quát trong khai triển: \(C_n^k\left(-\frac{1}{4}\right)^k.x^{n-k}\)
Số hạng chứa \(x^{n-2}\Rightarrow k=2\) có hệ số: \(C_n^k\left(-\frac{1}{4}\right)^k=\frac{1}{16}.C_n^2\)
\(\Rightarrow\frac{1}{16}.C_n^2=31\Rightarrow C_n^2=496\)
\(\Rightarrow\frac{n!}{2!.\left(n-2\right)!}=496\Leftrightarrow n\left(n-1\right)=992\)
\(\Leftrightarrow n^2-n-992=0\Rightarrow n=32\)
Theo công thức nhị thức Niu-tơn, ta có :
\(P=C_6^0\left(x-1\right)^6+C_6^1\left(x-1\right)^5+....+C_6^kx^{2k}\left(x-1\right)^{6-k}+....+C_6^5x^{10}\left(x-1\right)+C_6^6x^{12}\)
Suy ra, khi khai triển P thành đa thức, \(x^2\) chỉ xuất hiện khi khai triển \(C_6^0\left(x-1\right)^6\) và \(C_6^1\left(x-1\right)^5\)
Hệ số của \(x^2\) trong khai triển \(C_6^0\left(x-1\right)^6\) là : \(C_6^0.C_6^2\)
Hệ số của \(x^2\) trong khai triển \(C_6^1\left(x-1\right)^5\) là : \(-C_6^1.C_5^0\)
Vì vậy hệ số của \(x^2\) trong khai triển P thành đa thức là : \(C_6^0.C_6^2-C_6^1.C_5^0=9\)
Với số thực x ≠ 0 và với mọi số tự nhiên n ≥ 1, ta có:
(1 - 3x)n = [1 - (3x)]n =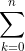
Ckn (1)n – k (-3)k . xk.
Suy ra hệ số của x2trong khai triển này là 32C2n .Theo giả thiết, ta có:
32C2n = 90 => C2n = 10.
Từ đó ta có:
⇔ n2 – n – 20 = 0 ⇔ n = -4 (loại) hoặc n = 5.
ĐS: n = 5.