Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
.
.
.
.
Chọn B
Phương trình hoành độ giao điểm 
.
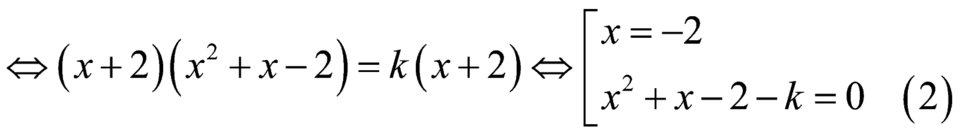Đường thẳng
cắt đồ thị hàm số 
tại 
điểm phân biệt
có hai nghiệm phân biệt khác 
Giả sử 
, 
là hai nghiệm phân biệt của 
, theo hệ thức Viet thì 
.
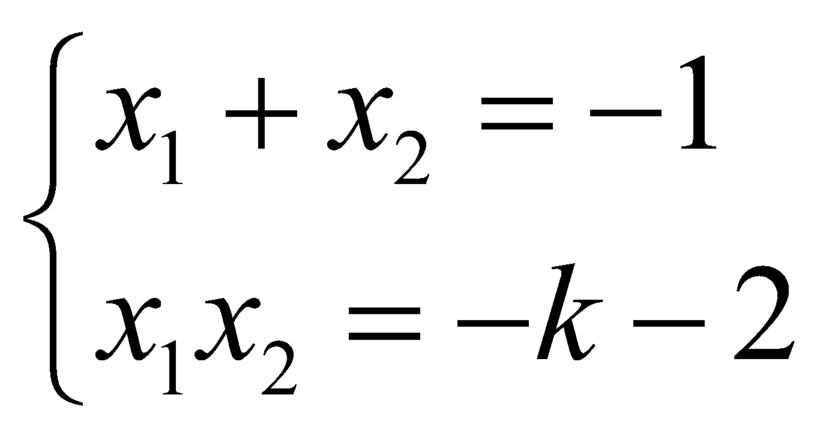Ta có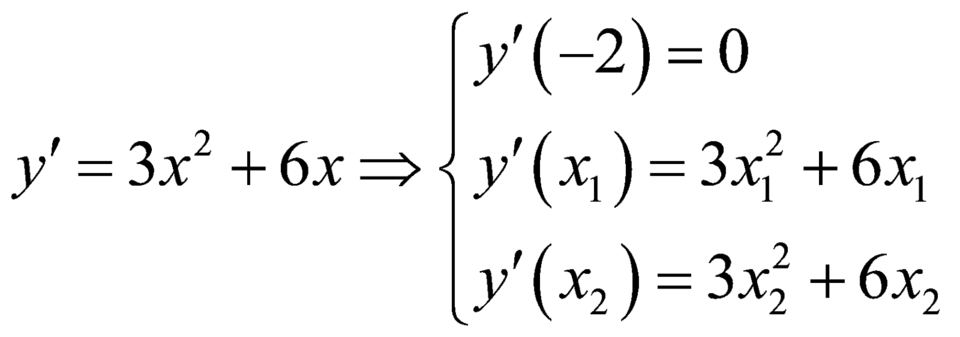 
.
Bài ra ta có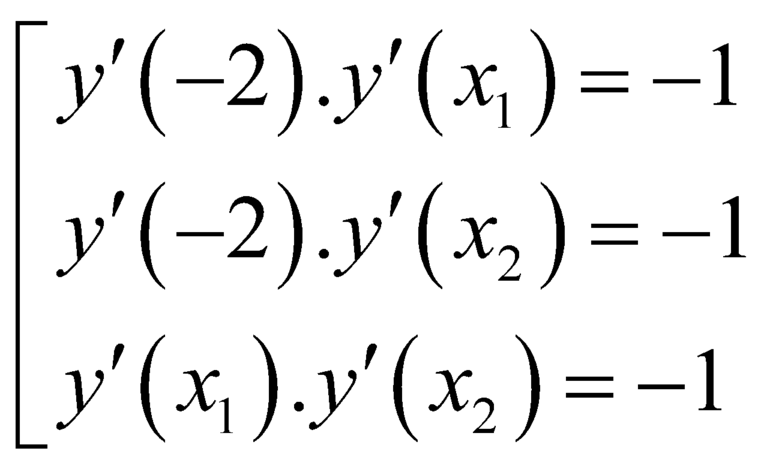 
.
Kết hợp với 
ta được 
thỏa mãn.
Phương trình hoành độ giao điểm
x3+2mx2+3(m-1)x+2 =-x+2 hay x(x2+2mx+3(m-1))=0
suy ra x=0 hoặc x2+2mx+3(m-1)=0 (1)
Đường thẳng d cắt (C) tại ba điểm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm phân biệt khác 0
⇔ m 2 - 3 m + 3 > 0 m - 1 ≠ 0 ⇔ ∀ m m ≠ 1 ⇔ m ≠ 1
Khi đó ta có: C( x1 ; -x1+2) ; B(x2 ; -x2+2) trong đó x1 ; x2 là nghiệm của (1) ; nên theo Viet thì x 1 + x 2 = - 2 m x 1 x 2 = 3 m - 3
Vậy
C B → = ( x 2 - x 1 ; - x 2 + x 1 ) ⇒ C B = 2 ( x 2 - x 1 ) 2 = 8 ( m 2 - 3 m + 3 )
d ( M ; ( d ) ) = - 3 - 1 + 2 2 = 2
Diện tích tam giác MBC bằng khi và chỉ khi
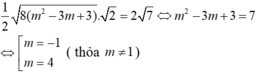
Chọn B.
2x3-3x2+1 =x-1 hay 2x3-3x2-x+2=0
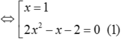
Khi đó ta có A(1 ; 0) ; B( x1 ; x1-1) và C( x2 ; x2-1) ( x1 ; x2 là nghiệm của (1))
Ta có 
, suy ra
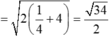
Chọn B.
.
.
.
.
Đáp án A
+ Phương trình hoành độ giao điểm: 
+ Điều kiện để d cắt tại hai điểm phân biệt là 
.
+ Trung điểm của MN là I.
+ Theo công thức đường trung tuyến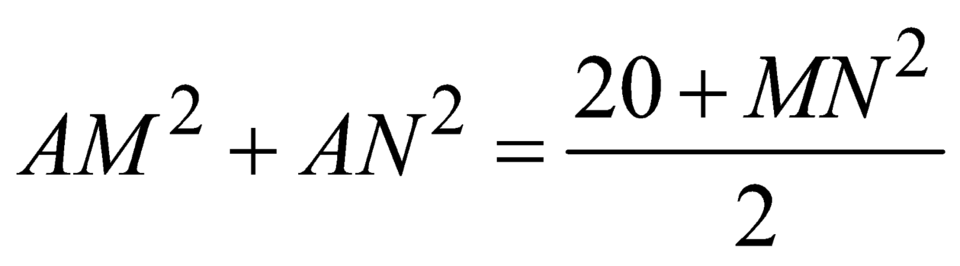 
.
nhỏ nhất khi 
nhỏ nhất.
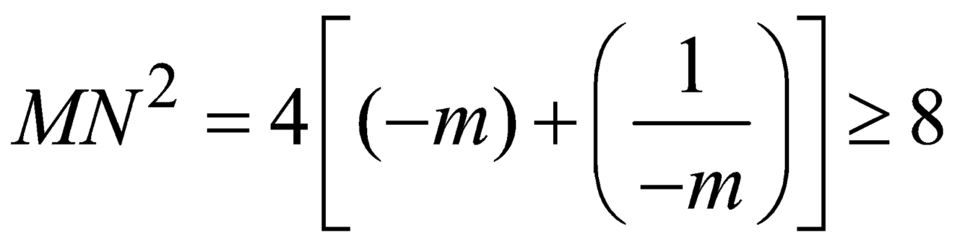, dấu bằng xảy ra khi 
Đường thẳng d đi qua A và có hệ số góc k nên có dạng y= k( x+ 1) hay
Kx- y+k=0 .
Phương trình hoành độ giao điểm của C và d là:
x 3 - 3 x 2 + 4 = k x + k ⇔ ( x + 1 ) ( x 2 - 4 x + 4 - k ) = 0
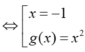
D cắt tại ba điểm phân biệt khi phương trình (*) có hai nghiệm phân biệt khác -1
⇔ ∆ ' > 0 g ( - 1 ) ≠ 0 ⇔ k > 0 k ≠ 9
Khi đó g( x) =0 khi x=2- k ; x = 2 + k Vậy các giao điểm của hai đồ thị lần lượt là
A ( - 1 ; 0 ) ; B ( 2 - k ; 3 k - k k ) ; C ( 2 + k ; 3 k + k k ) .
Tính được
B C = 2 k 1 + k 2 , d ( O , B C ) = d ( O , d ) = k 1 + k 2 .
Khi đó
S ∆ O B C = 1 2 . k k 2 + 1 . 2 k . k 2 + 1 = 1 ⇔ k k = 1 ⇔ k 3 = 1 ⇔ k = 1 .
Vậy k= 1 thỏa yêu cầu bài toán.
Chọn C.
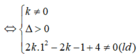
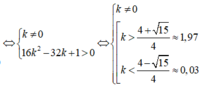
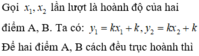
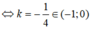
PT hoành độ giao điểm là
(3m-1) x+ 6m+ 3 == x3-3x2+ 1 hay x3-3x2 – (3m-1) x-6m-2=0 ( *)
Giả sử A( x1; y1) ; B( x2; y2) lần lượt là giao điểm của (C) và (d)
Vì B cách đều hai điểm A và C nên B là trung điểm của AC
Suy ra x1+ x3= 2x2
Thay x2= 1vào , ta có
Vậy -1< m< 0
Chọn C.