Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\frac{3}{16}.\frac{8}{15}-1,25\)
= \(\frac{1}{10}-\frac{125}{10}\)
= \(\frac{-124}{10}=\frac{-62}{5}\)
b) \(7,5.\frac{-5}{6}+4,5.\frac{-5}{6}\)
= \(\left(7,5+4,5\right).\frac{-5}{6}\)
= 12.\(\frac{-5}{6}\)
= -10

c1: EF=5cm
c2: EF=\(5\sqrt{2}\)cm
c3: \(DF=\sqrt{119}cm\)
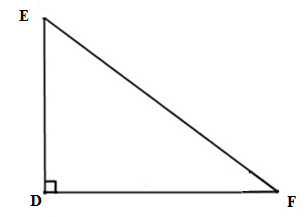
a) Xét \(\Delta EDF\) vuông tại \(D\left(gt\right)\) có:
\(EF^2=DE^2+DF^2\) (định lí Py - ta - go).
=> \(EF^2=3^2+4^2\)
=> \(EF^2=9+16\)
=> \(EF^2=25\)
=> \(EF=5\left(cm\right)\) (vì \(EF>0\)).
Vậy \(EF=5\left(cm\right).\)
b) Xét \(\Delta EDF\) vuông tại \(D\left(gt\right)\) có:
\(EF^2=DE^2+DF^2\) (định lí Py - ta - go).
=> \(EF^2=5^2+5^2\)
=> \(EF^2=25+25\)
=> \(EF^2=50\)
=> \(EF=\sqrt{50}\)
=> \(EF=5\sqrt{2}\left(cm\right)\) (vì \(EF>0\)).
Vậy \(EF=5\sqrt{2}\left(cm\right).\)
c) Xét \(\Delta EDF\) vuông tại \(D\left(gt\right)\) có:
\(EF^2=DE^2+DF^2\) (định lí Py - ta - go).
=> \(12^2=5^2+DF^2\)
=> \(DF^2=12^2-5^2\)
=> \(DF^2=144-25\)
=> \(DF^2=119\)
=> \(DF=\sqrt{119}\left(cm\right)\) (vì \(DF>0\)).
Vậy \(DF=\sqrt{119}\left(cm\right).\)
Chúc bạn học tốt!

a/
\(x-y=\frac{a}{b}-\frac{c}{d}=\frac{ad-cb}{bd}=\frac{1}{bd}.\) (1)
\(y-z=\frac{c}{d}-\frac{e}{h}=\frac{ch-de}{dh}=\frac{1}{dh}\)(2)
+ Nếu d>0 => (1)>0 và (2)>0 => x>y; y>x => x>y>z
+ Nếu d<0 => (1)<0 và (2)<0 => x<y; y<z => x<y<z
b/
\(m-y=\frac{a+e}{b+h}-\frac{c}{d}=\frac{ad+de-cb-ch}{d\left(b+h\right)}=\frac{\left(ad-cb\right)-\left(ch-de\right)}{d\left(b+h\right)}=\frac{1-1}{d\left(b+h\right)}=0\)
=> m=y
+
cảm ơn bn nha Nguyễn Ngoc Anh Minh mk k cho bn r đó kb vs mk nha
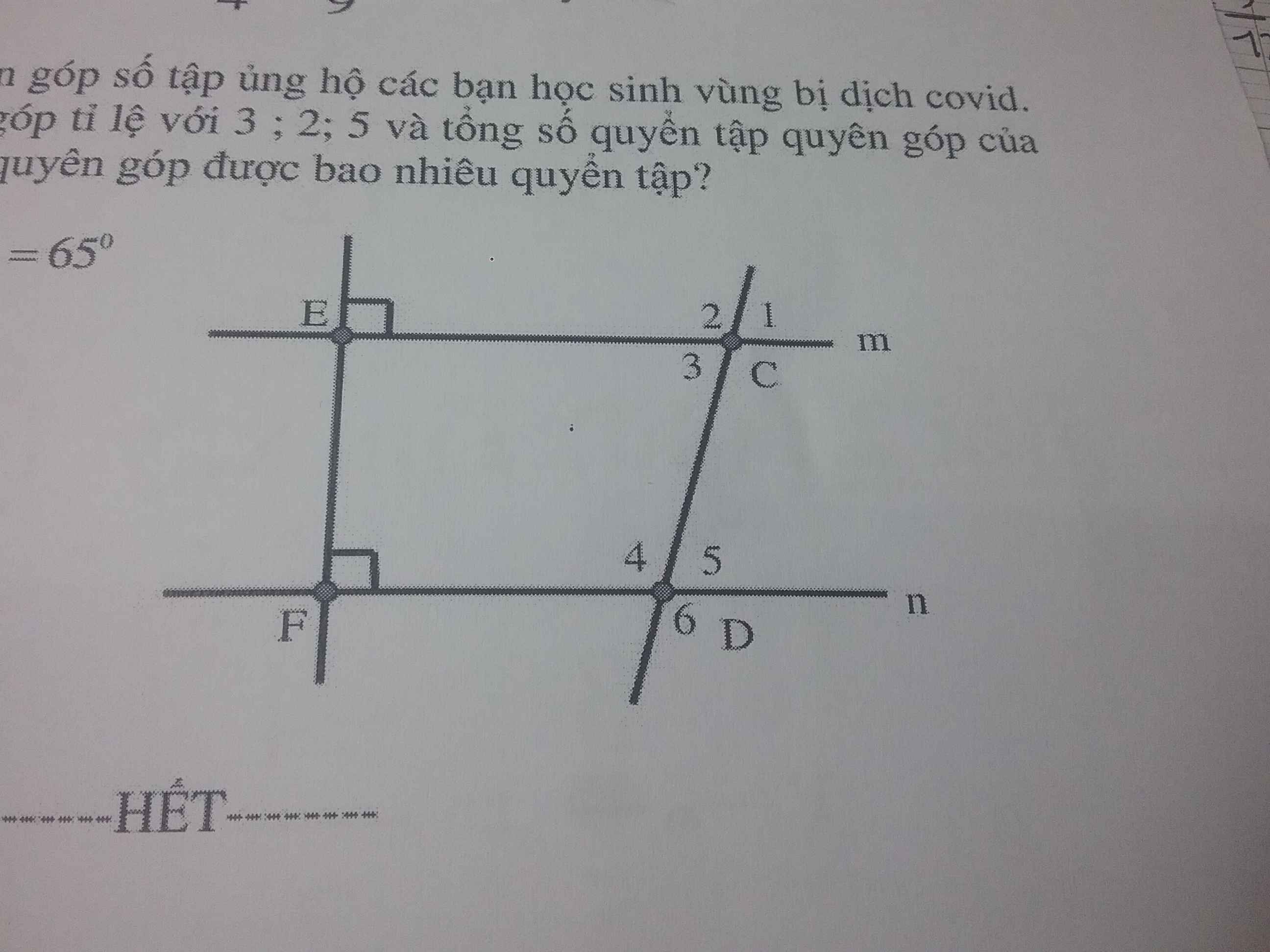
Ta có AB // Cx => ^BAC = ^C2 = 600 ( soletrong )
^C1 = 1800 - ^ABC - ^BAC = 1800 - 600 - 700 = 500
Ta có ^BCy là góc bẹt nên ^BCy = 1800
-> ^C3 = ^BCy - ^C1 - ^C2 = 1800 - 500 - 600 = 700