
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có \(\sqrt{8}+3< \sqrt{9}+3=3+3=6\)
=> \(\sqrt{8}+3< 6\)
Ta có \(\sqrt{48}< \sqrt{49};\sqrt{35}< \sqrt{36}\)
=> \(\sqrt{48}+\sqrt{35}< \sqrt{49}+\sqrt{46}\)
=> \(\sqrt{48}+\sqrt{35}< 13\)
=> \(\sqrt{48}< 13-\sqrt{35}\)
c) Ta có \(-\sqrt{19}< -\sqrt{17}\)
=> \(\sqrt{31}-\sqrt{19}< \sqrt{31}-\sqrt{17}\)
=> \(\sqrt{31}-\sqrt{19}< \sqrt{36}-17=6-\sqrt{17}\)
d) Ta có \(9=\sqrt{81}\Leftrightarrow\sqrt{81}>\sqrt{80}\);
\(-\sqrt{58}>-\sqrt{59}\)
=> \(\sqrt{81}-\sqrt{58}>\sqrt{80}-\sqrt{59}\)
<=> \(9-\sqrt{58}>\sqrt{80}-\sqrt{59}\)

a: \(\sqrt{17}+\sqrt{26}=\dfrac{9}{\sqrt{26}-\sqrt{17}}>9\)
e: \(\sqrt{13}-\sqrt{12}=\dfrac{1}{\sqrt{13}+\sqrt{12}}\)
\(\sqrt{12}-\sqrt{11}=\dfrac{1}{\sqrt{12}+\sqrt{11}}\)
mà \(\sqrt{13}+\sqrt{12}>\sqrt{11}+\sqrt{12}\)
nên \(\sqrt{13}-\sqrt{12}< \sqrt{12}-\sqrt{11}\)
d: \(9-\sqrt{58}=\sqrt{49}-\sqrt{58}< 0< \sqrt{80}-\sqrt{59}\)

a> \(\sqrt{25x}=35\)
⇔ \(5\sqrt{x}=35\)
⇔ \(\sqrt{x}=7\)
⇔ x=49
vậy x=49
b) \(4\sqrt{x}=\sqrt{48}\)
⇔ \(4\sqrt{x}=\sqrt{16}.\sqrt{3}\)
⇔ \(4\sqrt{x}=4\sqrt{3}\)
⇔ \(\sqrt{x}=\sqrt{3}\)
⇔ x=3
vậy x=3
\(\sqrt{144x}\le132\)
⇔ \(12\sqrt{x}\le132\)
⇔ \(\sqrt{x}\le11\)
⇔ x≤121
vậy x≤121
d \(3\sqrt{x}>\sqrt{10}\)
⇔ \(\sqrt{9x}>\sqrt{10}\)
⇔ 9x > 10
⇔ x > \(\dfrac{10}{9}\)
vậy x > \(\dfrac{10}{9}\)


a)√25x = 35
⇔5√x = 35
⇔√x = 7
⇔x = 49
b)√4x ≤ 162
⇔2√x ≤ 162
⇔√x ≤ 81
⇔x ≤ 6561
Suy ra : 0 ≤ x ≤ 6561
c)3√x = 12
⇔3√x = 2√3
⇔√x = 23√3
⇔x = (23√3)2
⇔x = −43
d) 2√x ≥ √10
⇔√x ≥ √102
⇔ x = 52

đặt b+c+d=x;c+d+a=y;d+a+b=z;a+b+c=t(a,b,c,d>0→x,y,z,t>0)
→a=\(\frac{x+y+z+t}{3}-x=\frac{x+y+z+t-3x}{3}\) tương tự ta có:b=\(\frac{x+y+z+t-3y}{3}\);c=\(\frac{x+y+z+t-3z}{3}\);d=\(\frac{x+y+z+t-3t}{3}\)
thay vào bt ta được:\(\frac{x+y+z+t-3x}{3x}+\frac{x+y+z+t-3y}{3y}+\frac{x+y+z+t-3z}{3z}+\frac{x+y+z+t-3t}{3t}\)
→\(\frac{1}{3}\left(1+\frac{y}{x}+\frac{z}{x}+\frac{t}{x}+\frac{x}{y}+1+\frac{z}{y}+\frac{t}{y}+\frac{x}{z}+\frac{y}{z}+1+\frac{t}{z}+\frac{x}{t}+\frac{y}{t}+\frac{z}{t}+1\right)-4\)
áp dụng định lý cô shi cho 2 số dương:(x,y,z,t>0)
s>=\(\frac{1}{3}\left(2+2+2+2+2+2+4\right)-4\)
s>=16/3-4→s>=\(\frac{4}{3}\)
\(\frac{a}{b+c+d}+\frac{b}{c+d+a}+\frac{c}{d+a+b}+\frac{d}{a+b+c}>\frac{4}{3}\)
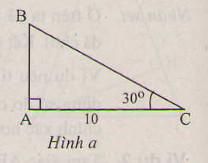
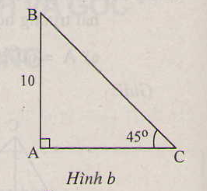
Chọn đáp án D.