Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Bất phương trình đã cho tương đương với hệ sau:
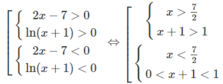
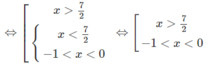
Vậy tập nghiệm là (−1;0) ∪ (7/2; + ∞ )
b) Tương tự câu a), tập nghiệm là (1/10; 5)
c) Đặt t = log 2 x , ta có bất phương trình 2 t 3 + 5 t 2 + t – 2 ≥ 0 hay (t + 2)(2 t 2 + t − 1) ≥ 0 có nghiệm −2 ≤ t ≤ −1 hoặc t ≥ 1/2
Suy ra 1/4 ≤ x ≤ 1/2 hoặc x ≥ 2
Vậy tập nghiệm của bất phương trình đã cho là: [1/4; 1/2] ∪ [ 2 ; + ∞ )
d) Bất phương trình đã cho tương đương với hệ:
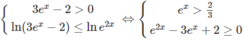
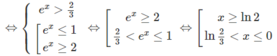
Vậy tập nghiệm là (ln(2/3); 0] ∪ [ln2; + ∞ )

\(A=\int\limits^{0.5}_{-0.5}cos\left[ln\left(\frac{1-x}{1+x}\right)\right]dx\) hay \(A=\int\limits^{0.5}_{-0.5}cos\left[\frac{ln\left(1-x\right)}{1+x}\right]dx\)
Dù thế nào thì có lẽ người ra đề cũng nhầm lẫn, đây là 1 bài toán ko thể giải quyết trong chương trình phổ thông, nếu hàm là hàm sin chứ ko phải cos thì còn có cơ hội làm được trong chương trình 12
Tích phân sửa lại như sau thì giải quyết được bằng phương pháp thông thường:
\(A=\int\limits^{0.5}_{-0.5}sin\left[ln\left(\frac{1-x}{1+x}\right)\right]dx\)
Vì hàm dưới dấu tích phân là hàm lẻ nên chỉ cần đặt \(x=-t\) sau đó đổi biến và cộng lại là suy ra ngay lập tức \(A=0\)
\(B=\int\limits^{\frac{\pi}{2}}_0\frac{cos^3x}{cos^3x+sin^3x}dx\) (1)
Đặt \(\frac{\pi}{2}-x=t\Rightarrow dx=-dt;\left\{{}\begin{matrix}x=0\Rightarrow t=\frac{\pi}{2}\\x=\frac{\pi}{2}\Rightarrow t=0\end{matrix}\right.\)
\(B=\int\limits^0_{\frac{\pi}{2}}\frac{sin^3t}{sin^3t+cos^3t}\left(-dt\right)=\int\limits^{\frac{\pi}{2}}_0\frac{sin^3t}{sin^3t+cos^3t}dt=\int\limits^{\frac{\pi}{2}}_0\frac{sin^3x}{sin^3x+cos^3x}dx\) (2)
Cộng vế với vế của (1) và (2):
\(2B=\int\limits^{\frac{\pi}{2}}_0\frac{sin^3x+cos^3x}{sin^3x+cos^3x}dx=\int\limits^{\frac{\pi}{2}}_0dx=\frac{\pi}{2}\Rightarrow B=\frac{\pi}{4}\)
c/ \(C=\int\limits^{\frac{\pi}{2}}_0\left(\sqrt{sinx}-\sqrt{cosx}\right)dx\) (1)
Đặt \(\frac{\pi}{2}-x=t\Rightarrow dx=-dt;\left\{{}\begin{matrix}x=0\Rightarrow t=\frac{\pi}{2}\\x=\frac{\pi}{2}\Rightarrow t=0\end{matrix}\right.\)
\(C=\int\limits^0_{\frac{\pi}{2}}\left(\sqrt{cost}-\sqrt{sint}\right)\left(-dt\right)=\int\limits^{\frac{\pi}{2}}_0\left(\sqrt{cost}-\sqrt{sint}\right)dt=\int\limits^{\frac{\pi}{2}}_0\left(\sqrt{cosx}-\sqrt{sinx}\right)dx\left(2\right)\)
Cộng vế với vế của (1) và (2):
\(2C=\int\limits^{\frac{\pi}{2}}_0\left(\sqrt{sinx}-\sqrt{cosx}+\sqrt{cosx}-\sqrt{sinx}\right)dx=0\)
\(\Rightarrow C=0\)
//Các dạng bài này đều giống nhau, nếu biểu thức đối xứng sin, cos và cận \(0;\frac{\pi}{2}\) thì đặt \(\frac{\pi}{2}-x=t\) rồi biến đổi và cộng lại

a)
Ta có \(A=\int ^{\frac{\pi}{4}}_{0}\cos 2x\cos^2xdx=\frac{1}{4}\int ^{\frac{\pi}{4}}_{0}\cos 2x(\cos 2x+1)d(2x)\)
\(\Leftrightarrow A=\frac{1}{4}\int ^{\frac{\pi}{2}}_{0}\cos x(\cos x+1)dx=\frac{1}{4}\int ^{\frac{\pi}{2}}_{0}\cos xdx+\frac{1}{8}\int ^{\frac{\pi}{2}}_{0}(\cos 2x+1)dx\)
\(\Leftrightarrow A=\frac{1}{4}\left.\begin{matrix} \frac{\pi}{2}\\ 0\end{matrix}\right|\sin x+\frac{1}{16}\left.\begin{matrix} \frac{\pi}{2}\\ 0\end{matrix}\right|\sin 2x+\frac{1}{8}\left.\begin{matrix} \frac{\pi}{2}\\ 0\end{matrix}\right|x=\frac{1}{4}+\frac{\pi}{16}\)
b)
\(B=\int ^{1}_{\frac{1}{2}}\frac{e^x}{e^{2x}-1}dx=\frac{1}{2}\int ^{1}_{\frac{1}{2}}\left ( \frac{1}{e^x-1}-\frac{1}{e^x+1} \right )d(e^x)\)
\(\Leftrightarrow B=\frac{1}{2}\left.\begin{matrix} 1\\ \frac{1}{2}\end{matrix}\right|\left | \frac{e^x-1}{e^x+1} \right |\approx 0.317\)
c)
Có \(C=\int ^{1}_{0}\frac{(x+2)\ln(x+1)}{(x+1)^2}d(x+1)\).
Đặt \(x+1=t\)
\(\Rightarrow C=\int ^{2}_{1}\frac{(t+1)\ln t}{t^2}dt=\int ^{2}_{1}\frac{\ln t}{t}dt+\int ^{2}_{1}\frac{\ln t}{t^2}dt\)
\(=\int ^{2}_{1}\ln td(\ln t)+\int ^{2}_{1}\frac{\ln t}{t^2}dt=\frac{\ln ^22}{2}+\int ^{2}_{1}\frac{\ln t}{t^2}dt\)
Đặt \(\left\{\begin{matrix} u=\ln t\\ dv=\frac{dt}{t^2}\end{matrix}\right.\Rightarrow \left\{\begin{matrix} du=\frac{dt}{t}\\ v=\frac{-1}{t}\end{matrix}\right.\Rightarrow \int ^{2}_{1}\frac{\ln t}{t^2}dt=\left.\begin{matrix} 2\\ 1\end{matrix}\right|-\frac{\ln t+1}{t}=\frac{1}{2}-\frac{\ln 2 }{2}\)
\(\Rightarrow C=\frac{1}{2}-\frac{\ln 2}{2}+\frac{\ln ^22}{2}\)

Lời giải:
Ta có:
\(A=\int \frac{x\sin x+\cos x}{x^2-\cos ^2x}dx=\int \frac{(\cos x-x)+x(\sin x+1)}{x^2-\cos ^2x}dx\)
\(=-\int \frac{dx}{\cos x+x}+\int \frac{x(\sin x+1)}{x^2-\cos ^2x}dx=-\int \frac{dx}{x+\cos x}+\frac{1}{2}\int (\sin x+1)\left(\frac{1}{x-\cos x}+\frac{1}{x+\cos x}\right)dx\)
\(=-\int \frac{dx}{x+\cos x}+\frac{1}{2}\int (\sin x+1)\frac{dx}{x-\cos x}+\frac{1}{2}\int (\sin x-1)\frac{dx}{x+\cos x}+\int \frac{dx}{x+\cos x}\)
\(=\frac{1}{2}\int (\sin x+1)\frac{dx}{x-\cos x}+\frac{1}{2}\int (\sin x-1)\frac{dx}{x+\cos x}\)
\(=\frac{1}{2}\int \frac{d(x-\cos x)}{x-\cos x}+\frac{1}{2}\int \frac{-d(x+\cos x)}{x+\cos x}\)
\(=\frac{1}{2}\ln |x-\cos x|-\frac{1}{2}\ln |x+\cos x|+c\)
Xét biểu thức $B$
\(B=\int \frac{\ln x-1}{x^2-\ln ^2x}dx=\int \frac{(\ln x-x)+(x-1)}{x^2-\ln ^2x}dx\)
\(=-\int \frac{dx}{x+\ln x}+\int \frac{x-1}{x^2-\ln ^2x}dx=-\int \frac{dx}{x+\ln x}+\frac{1}{2}\int \frac{(x-1)}{x}\left(\frac{1}{x-\ln x}+\frac{1}{x+\ln x}\right)dx\)
\(=-\int \frac{dx}{x+\ln x}+\frac{1}{2}\int \frac{1}{x-\ln x}.\frac{x-1}{x}dx+\frac{1}{2}\int \frac{1}{x+\ln x}.\frac{x-1}{x}dx\)
\(=-\int \frac{dx}{x+\ln x}+\frac{1}{2}\int \frac{1}{x-\ln x}.\frac{x-1}{x}dx-\frac{1}{2}\int \frac{1}{x+\ln x}.\frac{1+x}{x}dx+\int \frac{dx}{x+\ln x}\)
\(=\frac{1}{2}\int \frac{1}{x-\ln x}.\frac{x-1}{x}dx-\frac{1}{2}\int \frac{1}{x+\ln x}.\frac{1+x}{x}dx\)
\(=\frac{1}{2}\int \frac{d(x-\ln x)}{x-\ln x}-\frac{1}{2}\int \frac{d(x+\ln x)}{x+\ln x}\)
\(=\frac{1}{2}\ln |x-\ln x|-\frac{1}{2}\ln |x+\ln x|+c\)

Câu 1: Là \(ln^2x+lnx\) hay \(lnx^2+lnx\) bạn, hai cái này khác nhau lắm, viết thế kia chẳng hiểu gì cả. Biểu thức logarit nếu viết mũ, thì hoặc là viết thế này \(ln^2x\) hoặc là \(\left(lnx\right)^2\), nếu viết \(ln\left(x\right)^2\) người ta sẽ mặc định hiểu là \(ln\left(x^2\right)\)
Chắc là cái đầu, vậy ta biến đổi được:
\(lnx\left(lnx+1\right)=lnx\left(lnx+lne\right)=lnx.ln\left(x.e\right)=ln\left(x.e\right)^{lnx}\)
Câu 2: đạo hàm 4 cái ra, dễ dàng nhận ra ở đáp án d, với \(x\ge0\Rightarrow f'\left(x\right)=3x^2+4x+\frac{1}{2\sqrt{x}}>0\) luôn đồng biến nên hàm không có cực trị
Câu 3:
Phương trình hoành độ giao điểm:
\(\frac{m-x}{x+1}=2x+m\Leftrightarrow m-x=2x^2+\left(m+2\right)x+m\)
\(\Leftrightarrow2x^2+\left(m+3\right)x=0\)
Phương trình luôn có nghiệm \(x=0\) hay ít nhất 1 trong 2 điểm A; B sẽ trùng gốc tọa độ tức \(OA=0\) hoặc \(OB=0\)
Do đó ko tồn tại m thỏa mãn
Câu 4:
\(\left\{{}\begin{matrix}lnx=X\\lny=Y\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}2X^2+3Y^2=5\\X+4Y=3\end{matrix}\right.\)
\(\Rightarrow2\left(3-4Y\right)^2+3Y^2=5\)
\(\Leftrightarrow35Y^2-48Y+13=0\Rightarrow\left[{}\begin{matrix}Y=1\Rightarrow X=-1\\Y=\frac{13}{35}\Rightarrow X=\frac{53}{35}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}lnx=-1\\lny=1\end{matrix}\right.\) \(\Rightarrow\left(x;y\right)=\left(e^{-1};e\right)\) \(\Rightarrow\left\{{}\begin{matrix}c=-1\\d=1\end{matrix}\right.\)
Hoặc \(\left\{{}\begin{matrix}lnx=\frac{53}{35}\\lny=\frac{13}{35}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=e^{\frac{53}{35}}=e\sqrt[35]{e^{18}}\\y=e^{\frac{13}{35}}=\sqrt[35]{e^{13}}\end{matrix}\right.\) \(\Rightarrow a=b=35\)
Đáp án b sai

a) Điều kiện: \(\left\{{}\begin{matrix}4x+2>0\\x-1>0\\x>0\end{matrix}\right.\)
Hay là: \(x>1\)
Khi đó biến đổi pương trình như sau:
\(\ln\dfrac{4x+2}{x-1}=\ln x\)
\(\Leftrightarrow\dfrac{4x+2}{x-1}=x\)
\(\Leftrightarrow4x+2=x\left(x-1\right)\)
\(\Leftrightarrow x^2-5x-2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x_1=\dfrac{5+\sqrt{33}}{2}\\x_2=\dfrac{5-\sqrt{33}}{2}\left(loại\right)\end{matrix}\right.\)
Vậy nghiệm của phương trình là: \(x=\dfrac{5+\sqrt{33}}{2}\)
b) Điều kiện: \(\left\{{}\begin{matrix}3x+1>0\\x>0\end{matrix}\right.\)
Hay là: \(x>0\)
Biến đổi phương trình như sau:
\(\log_2\left(3x+1\right)\log_3x-2\log_2\left(3x+1\right)=0\)
\(\Leftrightarrow\log_2\left(3x+1\right)\left(\log_3x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\log_2\left(3x+1\right)=0\\\log_3x=2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x+1=2^0\\x=3^2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(loại\right)\\x=9\end{matrix}\right.\)
Vậy nghiệm là x = 9.

`a)TXĐ:R\\{1;1/3}`
`y'=[-4(6x-4)]/[(3x^2-4x+1)^5]`
`b)TXĐ:R`
`y'=2x. 3^[x^2-1] ln 3-e^[-x+1]`
`c)TXĐ: (4;+oo)`
`y'=[2x-4]/[x^2-4x]+2/[(2x-1).ln 3]`
`d)TXĐ:(0;+oo)`
`y'=ln x+2/[(x+1)^2].2^[[x-1]/[x+1]].ln 2`
`e)TXĐ:(-oo;-1)uu(1;+oo)`
`y'=-7x^[-8]-[2x]/[x^2-1]`
Lời giải:
a.
$y'=-4(3x^2-4x+1)^{-5}(3x^2-4x+1)'$
$=-4(3x^2-4x+1)^{-5}(6x-4)$
$=-8(3x-2)(3x^2-4x+1)^{-5}$
b.
$y'=(3^{x^2-1})'+(e^{-x+1})'$
$=(x^2-1)'3^{x^2-1}\ln 3 + (-x+1)'e^{-x+1}$
$=2x.3^{x^2-1}.\ln 3 -e^{-x+1}$
c.
$y'=\frac{(x^2-4x)'}{x^2-4x}+\frac{(2x-1)'}{(2x-1)\ln 3}$
$=\frac{2x-4}{x^2-4x}+\frac{2}{(2x-1)\ln 3}$
d.
\(y'=(x\ln x)'+(2^{\frac{x-1}{x+1}})'=x(\ln x)'+x'\ln x+(\frac{x-1}{x+1})'.2^{\frac{x-1}{x+1}}\ln 2\)
\(=x.\frac{1}{x}+\ln x+\frac{2}{(x+1)^2}.2^{\frac{x-1}{x+1}}\ln 2\\ =1+\ln x+\frac{2^{\frac{2x}{x+1}}\ln 2}{(x+1)^2}\)
e.
\(y'=-7x^{-8}-\frac{(x^2-1)'}{x^2-1}=-7x^{-8}-\frac{2x}{x^2-1}\)

a/ Tích phân này làm sao giải được nhỉ?
b/ Đặt \(\sqrt{x}=t\Rightarrow x=t^2\Rightarrow dx=2t.dt\)
\(I=\int\frac{2t^2.dt}{4-t^4}=\int\left(\frac{1}{2-t^2}-\frac{1}{2+t^2}\right)dt=\frac{1}{2\sqrt{2}}ln\left|\frac{\sqrt{2}+t}{\sqrt{2}-t}\right|+\frac{1}{\sqrt{2}}arctan\frac{\sqrt{2}}{t}+C\)
\(=\frac{1}{2\sqrt{2}}ln\left|\frac{\sqrt{2}+\sqrt{x}}{\sqrt{2}-\sqrt{x}}\right|+\frac{1}{\sqrt{2}}arctan\frac{\sqrt{2}}{\sqrt{x}}+C\)
c/ \(I=\int\frac{\sqrt{1+x^2}}{x^2}.xdx\)
Đặt \(\sqrt{1+x^2}=t\Rightarrow x^2=t^2-1\Rightarrow xdx=tdt\)
\(\Rightarrow I=\int\frac{t^2dt}{t^2-1}=\int\left(1+\frac{1}{t^2-1}\right)dt=t+ln\left|\frac{t-1}{t+1}\right|+C=\sqrt{1+x^2}+ln\left|\frac{\sqrt{1+x^2}-1}{\sqrt{1+x^2}+1}\right|+C\)
d/ Con nguyên hàm này cũng không tính được, chắc bạn ghi nhầm đề


Đáp án C