K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HH
1
CM
10 tháng 2 2019
Thử trực tiếp ta thấy ngay x = -3 là nghiệm của bất phương trình (1) nhưng không là nghiệm bất phương trình (2), vì vậy (1) và (2) không tương đương do đó phép bình phương hai vế một bất phương trình không phải là phép biến đổi tương đương.
BT
8 tháng 5 2017
Thay \(x=-3\) vào bất phương trình (1) ta được:
\(3.\left(-3\right)+1< -3+3\)\(\Leftrightarrow-8< 0\) ( đúng)
Vậy \(x=-3\) là nghiệm của bất phương trình (1)
TThay \(x=-3\) vào bất phương trình (2) ta được:
\(\left(3.\left(-3\right)+1\right)^2< \left(-3+3\right)^2\)\(\Leftrightarrow64< 0\) (vô lý).
Vậy \(x=-3\) là nghiệm của bất phương trình (2).
Vậy hai bất phương trình (1) và (2) không tương đương và bình phương hai vế của bất phương trình không là phép biến đổi tương đương.
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 3 2021
\(\Leftrightarrow x^2-2x-m+\dfrac{2\left(x^2-2x-m\right)\left(\sqrt{x}+1\right)}{x+\sqrt{2x+m}}=0\)
\(\Leftrightarrow\left(x^2-2x-m\right)\left(1+\dfrac{2\left(\sqrt{x}+1\right)}{x+\sqrt{2x+m}}\right)=0\)
\(\Leftrightarrow x^2-2x-m=0\)
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
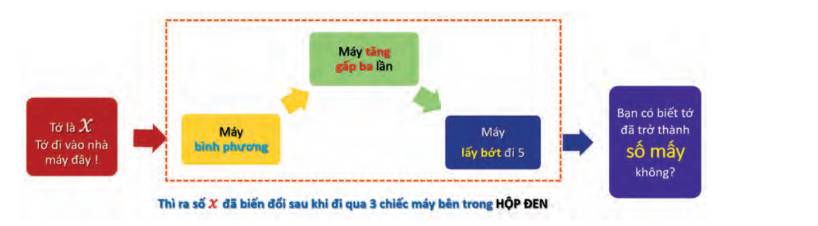
Sau khi vào hộp đen, x đi qua:
+) Đầu tiên, x đi qua hộp màu vàng (bình phương), ta được \({x^2}\)
+) Tiếp tục, \({x^2}\) đi qua hộp màu xanh lá (tăng gấp ba lần), ta được \(3{x^2}\)
+) Cuối cùng, \(3{x^2}\) đi qua hộp màu xanh dương (bớt đi 5), ta được: \(3{x^2} - 5\)
Như vậy sau khi đi qua HỘP ĐEN, số x đã biến đổi thành số \(3{x^2} - 5\)
Kiểm tra lại với số 2: theo công thức thì sau khi qua hộp đen ta được số: \({3.2^2} - 5 = 7\)(đúng).
Vậy biểu thức f(x) mô tả sự biến đổi đã tác động lên x là: \(f(x) = 3{x^2} - 5.\)
AH
Akai Haruma
Giáo viên
26 tháng 8 2021
Lời giải
$y'=3x^2+1>0$ với mọi $x\in\mathbb{R}$ nên hàm $y=x^3+x$ đồng biến trên $\mathbb{R}$
PT $\Leftrightarrow x^3+x=\sqrt[3]{2x+1}+2x+1$
Đặt $\sqrt[3]{2x+1}=t$ thì:
$x^3+x=t^3+t$
Vì hàm $y=x^3+x$ đồng biến nên $x^3+x=t^3+t\Leftrightarrow x=t$
$\Leftrightarrow x=\sqrt[3]{2x+1}$
$\Leftrightarrow x^3=2x+1$
Giải pt này dễ dàng có $x=-1; \frac{1\pm \sqrt{5}}{2}$
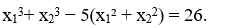
\(x_1^3+x_2^3-5\left(x_1^2+x_2^2\right)=26\)
\(\Leftrightarrow\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)-5\left[\left(x_1+x_2\right)^2-2x_1x_2\right]=26\)
\(\Leftrightarrow\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)-5\left(x_1+x_2\right)^2+10x_1x_2=26\)
Dạ e cảm ơn ạ