Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Hướng dẫn:
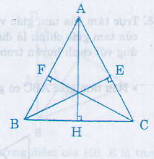
Xét hai tam giác vuông EBC và FCB có:
BC (cạnh huyền chung)
BE = CF (giả thiết)
Vậy ∆EBC = ∆FCB (cạnh huyền cạnh góc vuông)
=> \(\widehat{FBC}=\widehat{ECB}\)
hay ∆ABC cân tại A
+ Nếu tam giác có ba đường cao bằng nhau, tương tự như chứng minh trên, ta chứng minh được ba góc của chúng bằng nhau, suy ra đó là tam giác đều.
Bạn Thien Tu Borum làm nhanh vô rồi sai hình thức rồi kìa
Vẽ BH⊥ACvà CK⊥AB
Xét hai tam giác vuông KBC và HCB có:
Cạnh BC chung
BH=CK(gt)
⇒ΔKBC=ΔHCB
⇒KBCˆ=HCBˆ
Xét tam giác ABC, có:
KBCˆ=HCBˆ hay ABCˆ=ACBˆ
Vậy tam giác ABC cân tại A (đpcm)
Ba đường cao bằng nhau
Từ a) ta có:
Nếu BH = CK thì ΔABC cân tại A => AB = AC (1)
Nếu AI = BH thì ΔABC cân tại C => CA = CB (2)
Từ (1) và (2) ta có: AB = BC = AC
Vậy ΔABC là tam giác đều.
Xét hai tam giác vuông EBC và FCB có:
BC (cạnh huyền chung)
BE = CF
Vậy ∆EBC = ∆FCB (cạnh huyền cạnh góc vuông)
\(\Rightarrow\widehat{FBC}=\widehat{ECB}\)
hay ∆ABC cân tại A
+ Nếu tam giác có ba đường cao bằng nhau, tương tự như chứng minh trên, ta chứng
minh được đó là tam giác đều.