Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
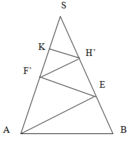
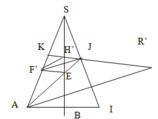
Gọi F’,H’ là điểm đối xứng của F,H qua SO
( O là tâm của đáy)
⇒ EF'=EF, FH=F'H'
Gọi I,J là điểm đối xứng của A,F’ qua SB
⇒
EF
'
=
EJ
,
F
'
H
'
=
H
'
J
A
E
+
EF'+F'H'+H'K=AE+EJ
+
H
'
J
+
H
'
K
≥
AJ
+
K
J
Gọi R là điểm đối xứng của A qua SI ⇒ AJ = J R
⇒
AJ
+
K
J
=
J
R
+
K
J
≥
K
R
Vậy để AE+EF’+F’H’+H’K nhỏ nhất bằng KR thì
H
'
J
+
H
'
K
=
K
J
A
E
+
EJ
=
AJ
=
J
R
k
=
H
F
+
H
K
E
A
+
EF
=
H
'
F
'
+
H
'
K
E
A
+
EF'
=
K
J
J
R
=
S
K
S
A
=
1
2

Chọn đáp án B
Do S.ABCD là hình chóp tứ giác đều nên mỗi mặt bên là một tam giác cân tại đỉnh S.
Theo giả thiết ta có
![]()
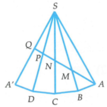
Cắt hình chóp theo cạnh bên SA rồi trải các mặt bên thành một mặt phẳng ta được hình vẽ bên sao cho khí ghép lại thì A ≡ A '
Suy ra A S A ' ⏜ = 4 . A S B ⏜ = π 3 và ∆ S A A ' đều cạnh SA = a

Khi đó tổng AM + MN + NP + PQ là tổng của các đường gấp khúc.
Tổng này đạt nhỏ nhất bằng AQ nếu xảy ra trường hợp các điểm A, M, N, P, Q thẳng hàng.
Mà ∆ S A A ' đều có Q là trung điểm SA nên A Q = S A 3 2 = a 3 2
Vậy m i n A M + M N + N P + P Q = a 3 2

Lời giải:
a) Gọi phương trình đường thẳng có dạng $y=ax+b$ $(d)$
Vì \(B,C\in (d)\Rightarrow \left\{\begin{matrix} 3=2a+b\\ -3=-4a+b\end{matrix}\right.\Rightarrow \left\{\begin{matrix} a=1\\ b=1\end{matrix}\right.\Rightarrow y=x+1\)
Vậy PT đường thẳng chứa cạnh $BC$ có dạng $y=x+1$
b) Tương tự, ta lập được phương trình đường thẳng chứa cạnh $AC$ là \((d_1):y=\frac{2x}{5}-\frac{7}{5}\).
Gọi PT đường cao đi qua $B$ của tam giác $ABC$ là \((d'):y=ax+b\)
Vì \((d')\perp (d_1)\Rightarrow \frac{2}{5}a=-1\Rightarrow a=\frac{-5}{2}\).
Mặt khác \(B\in (d')\Rightarrow 3=\frac{-5}{2}.2+b\Rightarrow b=8\)
\(\Rightarrow (d'):y=\frac{-5x}{2}+8\)
c) Gọi điểm thỏa mãn ĐKĐB là $M(a,b)$
Ta có: \(M\in (\Delta)\Rightarrow 2a+b-3=0\) $(1)$
$M$ cách đều $A,B$ \(\Rightarrow MA^2=MB^2\Rightarrow (a-1)^2+(b+1)^2=(a-2)^2+(b-3)^2\)
\(\Leftrightarrow 2-2a+2b=13-4a-6b\)
\(\Leftrightarrow 11-2a-8b=0(2)\)
Từ \((1);(2)\Rightarrow \left\{\begin{matrix} a=\frac{13}{14}\\ b=\frac{8}{7}\end{matrix}\right.\Rightarrow M\left ( \frac{13}{14};\frac{8}{7} \right )\)
con nếu đề bài cho 1 điểm và phương trình đường thẳng của tam giác muốn tìm phương trình đường cao còn lại vầ các cạnh thj làm thế nào

a: \(\text{Δ}ABC\sim\text{Δ}HBA;\text{Δ}ABC\sim\text{Δ}HCA\)
b: \(BC=\sqrt{AB^2+AC^2}=25\left(cm\right)\)
\(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{15\cdot20}{25}=12\left(cm\right)\)
\(BH=\dfrac{AB^2}{BC}=\dfrac{15^2}{25}=9\left(cm\right)\)
CH=BC-BH=25-9=16(cm)




Đáp án A
Phương pháp:
Trải 4 mặt của hình chóp ra mặt phẳng và tìm điều kiện để A M + M N + N P + P Q là nhỏ nhất.
Cách giải:
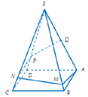
Ta “xếp” 4 mặt của hình chóp lên một mặt phẳng, được như hình bên:
Như hình vẽ ta tháy, để tiết kiệm dây nhất thì các đoạn AM, MN, NP, PQ phải tạo thành một đoạn thẳng AQ.
Lúc này, xét Δ S A Q có:
A S M = M S N = N S P = P S Q = 15 °
S A = 600 m , S Q = 300 m
⇒ k = A M + M N N P + P Q = A N N Q = S A S Q = 2
(Vì A N N Q = S A S Q do tính chất của đường phân giác SN).