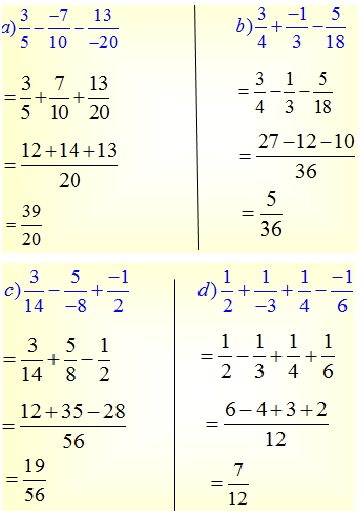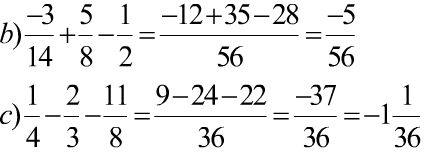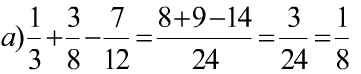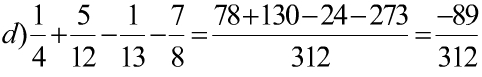Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)\(=\dfrac{211}{180}\)
b)\(=\dfrac{5}{39}\)
c)=\(=-\dfrac{65}{168}\)
Câu a:
\(\frac{1}{15}\) + \(\frac{1}{35}\) + \(\frac{1}{63}\) + \(\frac{1}{99}\) + \(\frac{1}{143}\)
= \(\frac{1}{3.5}\) + \(\frac{1}{5.7}\) + \(\frac{1}{7.9}\) + \(\frac{1}{9.11}\) + \(\frac{1}{11.13}\)
= \(\frac12.\left(\frac{2}{3.5}+\frac{2}{5.7}+\frac{2}{7.9}+\frac{2}{9.11}+\frac{2}{11.13}\right)\)
= \(\frac12\).(\(\frac13-\frac15+\frac15-\frac17+\frac17-\frac19+\frac19-\frac{1}{11}+\frac{1}{11}-\frac{1}{13})\)
= \(\frac12\).(\(\frac13\) - \(\frac{1}{13}\))
= \(\frac12\).(\(\frac{13}{39}-\frac{3}{39})\)
= \(\frac12\).\(\frac{10}{39}\)
= \(\frac{5}{39}\)

d, Vì B=10^1993+1/10^1992+1 > 1 =>10^1993+1/10^1992+1>10^1993+1+9/10^1992+1+9 = 10^1993+10/10^1992+10= 10. (10^1992+1)/10. (10^1991+1) = 10^1992+1/10^1991+1=A Vậy A=B
cau d B>1 ta co tinh chat (\(\dfrac{a}{b}>\dfrac{a+m}{b+m}\) ) B> \(\dfrac{10^{1993}+1+9}{10^{1992}+1+9}\)\(=\dfrac{10^{1993}+10}{10^{1992}+10}\)=\(\dfrac{10\left(10^{1992}+1\right)}{10\left(10^{1991}+1\right)}\)=\(\dfrac{10^{1992}+1}{10^{1991}+1}\)=A
Suy ra B>A(chuc ban hoc goi nhe)

\(A=15.\left(\dfrac{3}{5}-\dfrac{2}{3}\right)+1\\ A=15.\left(\dfrac{9}{15}-\dfrac{10}{15}\right)+1\\ A=15.\dfrac{-1}{15}+1\\ A=-1+1\\ A=0\)
\(C=\dfrac{-5}{7}.\dfrac{2}{11}+\dfrac{-5}{7}.\dfrac{9}{11}+1\dfrac{5}{7}\\ C=\dfrac{-5}{7}.\dfrac{2}{11}+\dfrac{-5}{9}.\dfrac{9}{11}+\dfrac{12}{7}\\ C=\dfrac{-5}{7}.\left(\dfrac{2}{11}+\dfrac{9}{11}\right)+\dfrac{12}{7}\\ C=\dfrac{-5}{7}.1+\dfrac{12}{7}\\ C=\dfrac{-5}{7}+\dfrac{12}{7}\\ C=1\)

b, \(K =\) \(\dfrac{75}{100}+\dfrac{18}{21}+\dfrac{19}{32}+\dfrac{1}{4}+\dfrac{3}{21}+\dfrac{13}{32}\)
\(K = \) \(\dfrac{3}{4}+\dfrac{18}{21}+\dfrac{19}{32}+\dfrac{1}{4}+\dfrac{3}{21}+\dfrac{13}{32}\)
\(K = \) \(\left(\dfrac{3}{4}+\dfrac{1}{4}\right)+\left(\dfrac{18}{21}+\dfrac{3}{21}\right)+\left(\dfrac{19}{32}+\dfrac{13}{32}\right)\)
\(K = \) \(1 + 1 + 1\)
\(K = \) \(3\)

Câu a:
\(\frac27\) + \(\frac{-3}{8}\) + \(\frac{11}{7}\) + \(\frac17\) + \(\frac{5}{-8}\)
= (\(\frac27+\frac{11}{7}+\frac17\)) -(\(\frac38\) + \(\frac58\))
= (\(\frac{13}{7}+\frac17\)) - \(\frac88\)
= \(\frac{14}{7}-1\)
= 2 - 1
= 1
Câu b:
\(\frac{3}{17}+\frac{-5}{13}+\frac{-18}{35}+\frac{14}{17}+\frac{17}{-35}+\frac{-8}{13}\)
= (\(\frac{3}{17}+\frac{14}{17}\)) - (\(\frac{5}{13}\) + \(\frac{8}{13}\)) - (\(\frac{18}{35}+\frac{17}{35}\))
= \(\frac{17}{17}-\frac{18}{18}-\) \(\frac{35}{35}\)
= 1 - 1 - 1
= 0 - 1
= -1

a) \(\dfrac{1}{3}+\dfrac{3}{8}-\dfrac{7}{12}\)
\(=\dfrac{17}{24}-\dfrac{7}{12}\)
\(=\dfrac{1}{8}\)
b) \(\dfrac{-3}{14}+\dfrac{5}{8}-\dfrac{1}{2}\)
\(=\dfrac{23}{56}-\dfrac{1}{2}\)
\(=\dfrac{-5}{56}\)
c) \(\dfrac{1}{4}-\dfrac{2}{3}-\dfrac{11}{18}\)
\(=\dfrac{-5}{12}-\dfrac{11}{18}\)
\(=\dfrac{-37}{36}\)
d) \(\dfrac{1}{4}+\dfrac{5}{12}-\dfrac{1}{13}-\dfrac{7}{8}\)
\(=\dfrac{2}{3}-\dfrac{1}{13}-\dfrac{7}{8}\)
\(=\dfrac{23}{39}-\dfrac{7}{8}\)
\(=\dfrac{-89}{312}\)

A=\(\dfrac{2}{7}+\dfrac{-3}{8}+\dfrac{11}{7}+\dfrac{1}{3}+\dfrac{1}{7}+\dfrac{5}{-3}\)
A=\(\left(\dfrac{2}{7}+\dfrac{11}{7}+\dfrac{1}{7}\right)+\left(\dfrac{1}{3}+\dfrac{5}{-3}\right)+\dfrac{-3}{8}\)
A=\(2+\dfrac{-4}{3}+\dfrac{-3}{8}\)
A=\(\dfrac{7}{24}\)
B=\(\left(\dfrac{3}{17}+\dfrac{14}{17}\right)+\left(\dfrac{-18}{35}+\dfrac{17}{-35}\right)+\left(\dfrac{-5}{13}+\dfrac{-8}{13}\right)\)
B=\(\dfrac{17}{17}+\dfrac{-35}{35}+\dfrac{-13}{13}\)
B=\(1+\left(-1\right)+\left(-1\right)=-1\)
C=\(\dfrac{-3}{17}+\left(\dfrac{2}{3}+\dfrac{3}{17}\right)\)
C=\(\dfrac{-3}{17}+\dfrac{2}{3}+\dfrac{3}{17}=\left(\dfrac{-3}{17}+\dfrac{3}{17}\right)+\dfrac{2}{3}\)
C=0+\(\dfrac{2}{3}=\dfrac{2}{3}\)
D=\(\left(\dfrac{-1}{6}+\dfrac{5}{-12}\right)+\dfrac{7}{12}\)
D=\(\dfrac{-1}{6}+\dfrac{5}{-12}+\dfrac{7}{12}\)
D=\(\dfrac{-2}{12}+\dfrac{-5}{12}+\dfrac{7}{12}=\left(\dfrac{-2}{12}+\dfrac{-5}{12}\right)+\dfrac{7}{12}\)
D=\(\dfrac{-7}{12}+\dfrac{7}{12}=0\)

Tính để mai làm mà thoii kệ, làm luôn :vv
Giải:
\(B=\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+..+\dfrac{1}{19}\)
\(B=\dfrac{1}{4}+\left(\dfrac{1}{5}+\dfrac{1}{6}+..+\dfrac{1}{9}\right)+\left(\dfrac{1}{10}+\dfrac{1}{11}+...+\dfrac{1}{19}\right)\)
Vì \(\dfrac{1}{5}+\dfrac{1}{6}+..+\dfrac{1}{9}>\dfrac{1}{9}+\dfrac{1}{9}+...+\dfrac{1}{9}\)
Nên \(\dfrac{1}{5}+\dfrac{1}{6}+..+\dfrac{1}{9}>\dfrac{5}{9}>\dfrac{1}{2}\)
Vì \(\dfrac{1}{10}+\dfrac{1}{11}+...+\dfrac{1}{19}>\dfrac{1}{19}+\dfrac{1}{19}+...+\dfrac{1}{19}\)
Nên \(\dfrac{1}{10}+\dfrac{1}{11}+...+\dfrac{1}{19}>\dfrac{10}{19}>\dfrac{1}{2}\)
\(\Rightarrow B>\dfrac{1}{4}+\dfrac{1}{2}+\dfrac{1}{2}\)
\(\Rightarrow B=\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+...+\dfrac{1}{19}>1\)
Giải:
Ta có: \(B=\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}+...+\dfrac{1}{19}\)
\(=\dfrac{1}{4}+\left(\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+...+\dfrac{1}{19}\right)\)
Dễ thấy:
\(5< 20\Leftrightarrow\dfrac{1}{5}>\dfrac{1}{20}\)
\(6< 20\Leftrightarrow\dfrac{1}{6}>\dfrac{1}{20}\)
\(....................\)
\(19< 20\Leftrightarrow\dfrac{1}{19}>\dfrac{1}{20}\)
Cộng vế theo vế ta có:
\(B>\dfrac{1}{4}+\dfrac{1}{20}+\dfrac{1}{20}+\dfrac{1}{20}+...+\dfrac{1}{20}\) (có \(15\) phân số \(\dfrac{1}{20}\))
\(\Rightarrow B>\dfrac{1}{4}+\dfrac{1}{20}.15=\dfrac{1}{4}+\dfrac{3}{4}=1\)
Vậy \(B>1\) (Đpcm)

đây là tính nhanh à nếu tính bình thường thì tính may tính là ra
a) 17/23 . 8/16 . 23/17. (-80) . 3/4
= (17/23 . 23/17) . (8/16 . 3/4) . (-80)
= 1 . 3/8 . (-80)
= 3/8 . (-80)
= -30
b) 5/11 . 18/29 - 5/11 . 8/29 + 5/11 . 19/29
= 5/11 . (18/29 - 8/29 + 19/29)
= 5/11 . 1
= 5/11
c)(13/23 + 1313/2323 - 131313/232323).(1/3+1/4 -7/12)
= (13/23 + 1313/2323 - 131313/232323).0
= 0
d) 12/2x2 . 22/2x3 . 32/3x4 . 42/4x5 . 52/5x6 . 62/6x7 . 72/7x8 . 82/8x9 . 92/9x10
= 1/2 . 2/3 . 3/4 . 4/5 . 5/6 . 6/7 . 7/8 . 8/9 .9/10
= 1/10
Khó nhìn quá. Bạn thông cảm nhé! ![]()