Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

25xy mũ 2+55xy mũ 2+75 xy mũ 2=155 xy mũ 2
thông cảm nha telex của mình bị lỗi rồi T-T

TL:
= 19683 + 4 + 16 + 27 + 16
= 19687 + 32 + 27
= 19746
_HT_

x ( x - 2 ) + x - 2 = 0
x ( x - 2 ) + ( x - 2 ) . 1 = 0
( x - 2 ) ( x + 1 ) = 0
\(\Rightarrow\orbr{\begin{cases}x-2=0\\x+1=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=2\\x=-1\end{cases}}\)
Vậy x = 2 ; x = -1
\(x.x-2+x-2=0\)
\(\Leftrightarrow x-2.x+1=0\)
\(=x-2=0\Rightarrow x=0\)
\(=x+1\Rightarrow x=-1\)
\(\Rightarrow x=-1;x=2\)

Đây:
Ta có: \(2x+y+1=6\Rightarrow2x+y=5\)
Suy ra: \(4x+2y-1=\left(2x+y\right)+\left(2x+y\right)-1=5+5-1=9\)
Mik làm tắt nha bn tự trình bày lại cho hợp lí

A B C H M N I
HM _|_ AB (gt)
AB _|_ AC do tam giác ABC vuông tại A (gt)
AN; HM phân biệt
=> AN // HM (tc)
=> góc NAH = góc AHM (slt)
xét tam giác NAH và tam giác MHA có : AH chung
góc ANH = góc AMH = 90
=> tam giác NAH = tam giác MHA (ch-gn)
=> HM = AN (đn)
b, NA = HM (câu a)
xét tam giác NAM và tam giác HMA có : AM chung
góc NAM = góc HMA = 90
=> tam giác NAM = tam giác HMA (2cgv)
=> AH = MN (đn)
c, AN // HM (câu a)
=> góc NAH = góc AHM (slt) và góc ANM = góc NMH (slt)
xét tam giác NAI và tam giác MHI có : AN = MH (câu a)
=> tam giác NAI = tam giác MHI (g-c-g)
=> NI = IM (đn)
d, A B C H M N I

13+23+33+...+1003
=1+2+1.2.3+3+2.3.4+100+99.100.101
=(1+2+3+...+100)+(1.2.3+2.3.4+...+99.100.101)
=5050+101989800
=101994850
NHỚ T.I.C.K và KB với mk nha
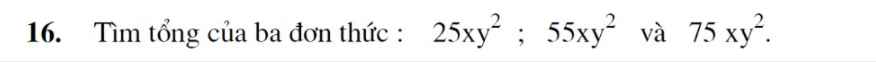 mn giúp mik vs ah mik rất cần
mn giúp mik vs ah mik rất cần
\(\sqrt{65}^2=65\)
\(\sqrt{65}=\sqrt{65}\)