Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt \(a=\dfrac{1}{x};b=\dfrac{1}{y};c=\dfrac{1}{z}\Rightarrow xyz=1\) và \(x;y;z>0\)
Gọi biểu thức cần tìm GTNN là P, ta có:
\(P=\dfrac{1}{\dfrac{1}{x^3}\left(\dfrac{1}{y}+\dfrac{1}{z}\right)}+\dfrac{1}{\dfrac{1}{y^3}\left(\dfrac{1}{z}+\dfrac{1}{x}\right)}+\dfrac{1}{\dfrac{1}{z^3}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)}\)
\(=\dfrac{x^3yz}{y+z}+\dfrac{y^3zx}{z+x}+\dfrac{z^3xy}{x+y}=\dfrac{x^2}{y+z}+\dfrac{y^2}{z+x}+\dfrac{z^2}{x+y}\)
\(P\ge\dfrac{\left(x+y+z\right)^2}{y+z+z+x+x+y}=\dfrac{x+y+z}{2}\ge\dfrac{3\sqrt[3]{xyz}}{2}=\dfrac{3}{2}\)
\(P_{min}=\dfrac{3}{2}\) khi \(x=y=z=1\) hay \(a=b=c=1\)
Đặt \(a = \frac{1}{x} ; b = \frac{1}{y} ; c = \frac{1}{z} \Rightarrow x y z = 1\) và \(x ; y ; z > 0\)
Gọi biểu thức cần tìm GTNN là P, ta có:
\(P = \frac{1}{\frac{1}{x^{3}} \left(\right. \frac{1}{y} + \frac{1}{z} \left.\right)} + \frac{1}{\frac{1}{y^{3}} \left(\right. \frac{1}{z} + \frac{1}{x} \left.\right)} + \frac{1}{\frac{1}{z^{3}} \left(\right. \frac{1}{x} + \frac{1}{y} \left.\right)}\)
\(= \frac{x^{3} y z}{y + z} + \frac{y^{3} z x}{z + x} + \frac{z^{3} x y}{x + y} = \frac{x^{2}}{y + z} + \frac{y^{2}}{z + x} + \frac{z^{2}}{x + y}\)
\(P \geq \frac{\left(\left(\right. x + y + z \left.\right)\right)^{2}}{y + z + z + x + x + y} = \frac{x + y + z}{2} \geq \frac{3 \sqrt[3]{x y z}}{2} = \frac{3}{2}\)
\(P_{m i n} = \frac{3}{2}\) khi \(x = y = z = 1\) hay \(a = b = c = 1\)

Diện tích đáy là: \(3.3 = 9\) (\(c{m^2}\))
Thể tích của hình chiếc hộp bánh là: \(\frac{1}{3}.9.2,5 = 7,5\) (\(c{m^3}\))

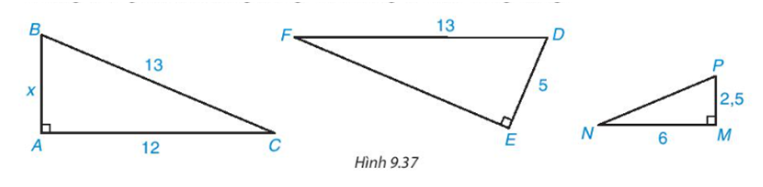
Những tam giác đồng dạng là
- Tam giác ABC đồng dạng với tam giác EDF với tỉ số đồng dạng là 1
- Tam giác MPN đồng dạng với tam giác ABC với tỉ số đồng dạng là \(\frac{1}{2}\)
- Tam giác MPN đồng dạng với tam giác EDF với tỉ số đồng dạng là \(\frac{1}{2}\)

Gọi x là khoảng cách từ A đến B (mét; x>0)
Số vòng quay của bánh trước là: \(\frac{x}{3}\)
Số vòng quay của bánh sau là: \(\frac{x}{3,2}\)
Vì khi máy kéo kéo từ A đến B bánh trước nhanh hơn bánh sau 30 vòng nên ta có phương trình sau:
\(\frac{x}{3}\)-\(\frac{x}{3,2}\)= 30
<=> 3,2x - 3x=288
<=>3,2x=288
=>x=90
Vậy khoảng cách AB là 90m
Em không chắc có đúng 100% hay không! Mong chị thông cảm!

a)
![]()
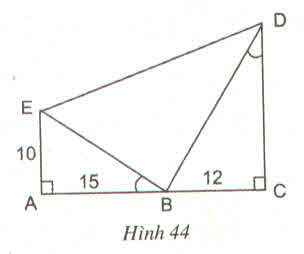
Vậy ∠EBD = 900
Vậy trong hình vẽ có ba tam giác vuông đó là:
∆ABE, ∆CBD, ∆EBD.
b) ∆ABE và ∆CDB có:
∠A = ∠C = 900
∠ABE = ∠CDB
=> ∆ABE ∽ ∆CDB => AB/CD = AE/CB
=> CD = AB.CB/AE
= 18 (cm)
∆ABE vuông tại A => BE =
![]() = 18 cm
= 18 cm
∆EBD vuông tại B => ED =
![]()
= 28,2 cm
c) Ta có: ![]()
= 1/2 . 10.15 + 1/2 . 12.18
= 75 + 108 = 183 cm2
SACDE = 1/2 (AE + CD).AC =1/2 (10+18).27=378 cm2
=> SEBD = SEBD – ( SABE + SDBC) = 378 – 183 = 195cm2




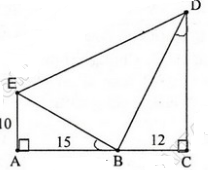


HELP ME
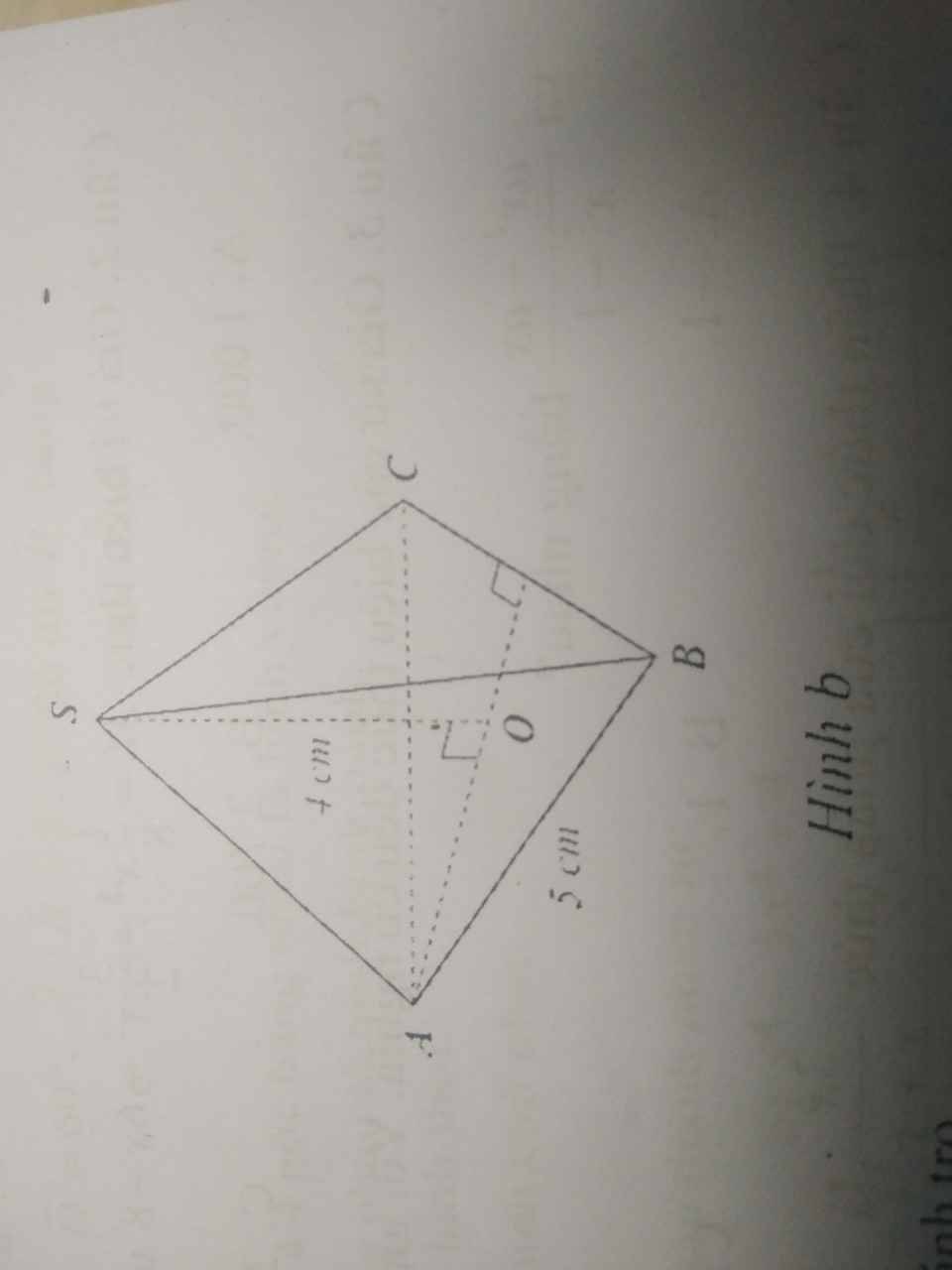
a: Kẻ AH\(\perp\)BC tại H
Ta có: ΔABC đều
mà AH là đường cao
nên \(AH=AB\cdot\dfrac{\sqrt{3}}{2}\)
=>\(AH=\dfrac{5\sqrt{3}}{2}\left(cm\right)\)
b: Diện tích đáy là:
\(S_{đáy}=AB^2\cdot\dfrac{\sqrt{3}}{4}=5^2\cdot\dfrac{\sqrt{3}}{4}=\dfrac{25\sqrt{3}}{4}\left(cm^2\right)\)
Thể tích của chiếc bánh tro là:
\(V=\dfrac{1}{3}\cdot4\cdot\dfrac{25\sqrt{3}}{4}=\dfrac{25\sqrt{3}}{3}\simeq14,4\left(cm^3\right)\)