Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khi bể nước có đáy thuộc mặt phẳng nằm ngang, thì mặt nước nằm trong mặt phẳng song song với đáy. Vì vậy, để đo độ sâu của bể, ta có thể đo khoảng cách từ mặt nước đến đáy bể.
Khi thả quả dọi vào bể nước, nó sẽ chìm dưới mặt nước và chạm đến đáy bể. Khi kéo quả dọi lên, ta sẽ thấy một đoạn dây dọi nằm trong bể nước và một đoạn dây dọi ở ngoài bể nước. Đoạn dây dọi nằm trong bể nước có độ dài bằng khoảng cách từ mặt nước đến chỗ quả dọi chạm đáy bể. Do đó, để đo độ sâu của bể, ta chỉ cần đo độ dài của đoạn dây dọi nằm trong bể nước.
Công thức để tính độ sâu của bể nước sẽ là:
Độ sâu bể = chiều dài của đoạn dây dọi nằm trong bể nước

tham khảo:
Đường thẳng vuông góc với mặt phẳng khi đường thẳng đó vuông góc với mọi đường thẳng thuộc mặt phẳng

tham khảo:
a) AO⊥xOy
b) Dây dọi vuông góc với 1 đường thẳng bất kì trong sàn nhà

tham khảo:
Thả sợi dây rọi từ điểm A trên trần nhà và đánh dấu điểm A' nơi đầu nhọn quả dọi chạm sàn
Thả sợi dây rọi từ điểm B trên trần nhà và đánh dấu điểm B' nơi đầu nhọn quả dọi chạm sàn
Ta có A'B' là hình chiếu vuông góc của AB trên trên nền nhà

THAM KHẢO:
Ta coi chân bàn như đường thẳng và mặt bàn, mặt sàn là 2 mặt phẳng.
Một chiếc bàn có các chân cùng vuông góc với mặt phẳng chứa mặt bàn và mặt phẳng chứa mặt sàn nên hai mặt phẳng đó có song song với nhau vì hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.

Đường thẳng d có vuông góc với mặt phẳng (P)
Vì: \(\left\{ \begin{array}{l}d \bot a\\d \bot b\\a \cap b\end{array} \right. \Rightarrow d \bot \left( P \right)\)

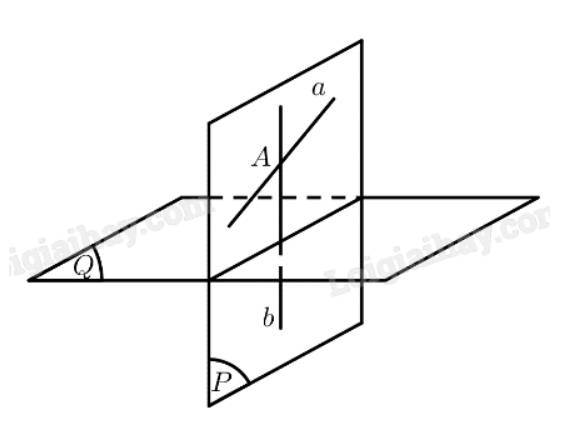
Cho đường thẳng \(a\) không vuông góc với mặt phẳng \(\left( Q \right)\). Ta cần chứng minh tồn tại duy nhật mặt phẳng \(\left( P \right)\) chứa đường thẳng \(a\) và vuông góc với mặt phẳng \(\left( Q \right)\).
• Lấy điểm \(A \in a\). Qua điểm \(A\) kẻ đường thẳng \(b\) vuông góc với mặt phẳng \(\left( Q \right)\).
\(\left. \begin{array}{l}b \bot \left( Q \right)\\b \in mp\left( {a,b} \right)\end{array} \right\} \Rightarrow mp\left( {a,b} \right) \bot \left( Q \right)\)
Vậy tồn tại mặt phẳng chứa đường thẳng \(a\) và vuông góc với mặt phẳng \(\left( Q \right)\).
• Giả sử có thêm mặt phẳng \(\left( P \right)\) chứa đường thẳng \(a\) và vuông góc với mặt phẳng \(\left( Q \right)\).
\( \Rightarrow a = \left( P \right) \cap mp\left( {a,b} \right)\)
Theo Bài tập 3b trang 99 ta có \(a \bot \left( Q \right)\), trái với giả thiết \(a\) không vuông góc với mặt phẳng \(\left( Q \right)\).
Vậy \(\left( P \right) \equiv mp\left( {a,b} \right)\).
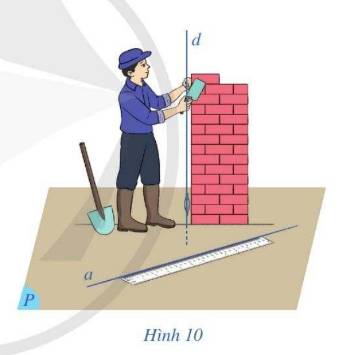


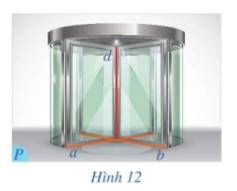
THAM KHẢO:
Khi dây dọi căng và mặt nước yên lặng, đường thẳng chứa dây dọi vuông góc với mặt phẳng chứa mặt nước trong thùng