Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử ta chọn hai phân số có cùng tử: và
.
Ta muốn có .
Thế thì a . a = a.(x + y). Từ đó suy ra x + y = a.
Vì vậy với mỗi a > 1 cho trước ta có thể chọn x và y sao cho x + y = a.
Chẳng hạn với a = 11, x = 5, y = 6 ta có:
Mặt khác, Vậy
.
Như vậy ta có thể tìm được vô số cặp phân số mà tổng và tích của chúng bằng nhau.

Tính các tổng dưới đây sau khi đã rút gọn phân số :
a)\(\dfrac{7}{21}\) + \(\dfrac{9}{-36}\) = \(\dfrac{7}{21}\)+\(\dfrac{-9}{36}\)=\(\dfrac{1}{3}\)+\(\dfrac{-1}{4}\)=\(\dfrac{4}{12}\)+\(\dfrac{-3}{12}\)=\(\dfrac{1}{12}\)
b) \(\dfrac{-12}{18}\)+\(\dfrac{-21}{35}\)=\(\dfrac{-2}{3}\)+\(\dfrac{-3}{5}\)=\(\dfrac{-10}{15}\)+\(\dfrac{-9}{15}\)=\(\dfrac{-19}{15}\)
c) \(\dfrac{-3}{21}\)+\(\dfrac{6}{42}\)=\(\dfrac{-1}{7}\)+\(\dfrac{1}{7}\)=0
d) \(\dfrac{-18}{24}\)+\(\dfrac{15}{-21}\)=\(\dfrac{-18}{24}\)+\(\dfrac{-15}{21}\)=\(\dfrac{-3}{4}\)+\(\dfrac{-5}{7}\)=\(\dfrac{-21}{28}\)+\(\dfrac{-20}{28}\)=\(\dfrac{-41}{28}\)

Ta có : 6 = 1 . 6 = 2 . 3; 35 = 5 . 7
Do đó ta có ba cách phân tích khác sau đây:
;
;
.

tính chất trên gọi là tính chất bắc cầu, ta so sánh hai phân số với một số (phân số) thứ 3.
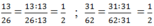
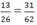
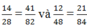

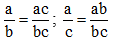
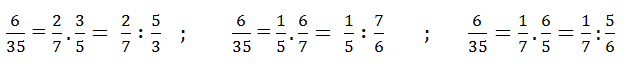
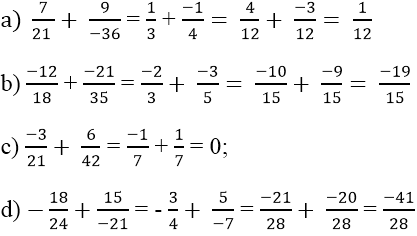
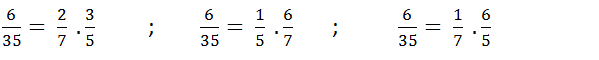
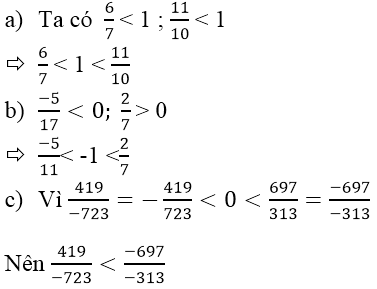
Phân số \(\frac{12}{48}=\frac{21}{84}\)